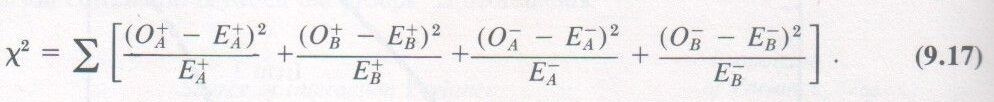Bias in Mental Testing (Jensen, 1980)

The scanned version of Jensen's book, Bias in Mental Testing, is available as a PDF. If you want my version though, email me at m h 1 9 8 7 0 4 1 0 @ g m a i l . c o m.

Bias in Mental Testing

Arthur R. Jensen (1980)

CONTENT [Jump links below]

Ch.6 Do IQ Tests Really Measure Intelligence?
A Realistic Example of Factor Analysis
Ch.7 Reliability and Stability of Mental Measurements
Causes of Score Instability
Ch.8 Validity and Correlates of Mental Tests
Occupational Level, Performance, and Income
Ch.9 Definitions and Criteria of Test Bias
Ch.10 Bias in Predictive Validity: Empirical Evidence
Test Bias in Predicting Scholastic Performance
Predictive Bias in the Armed Forces
Bias in the Test Prediction of Civilian Job Performances
Ch.11 Internal Criteria of Test Bias: Empirical Evidence
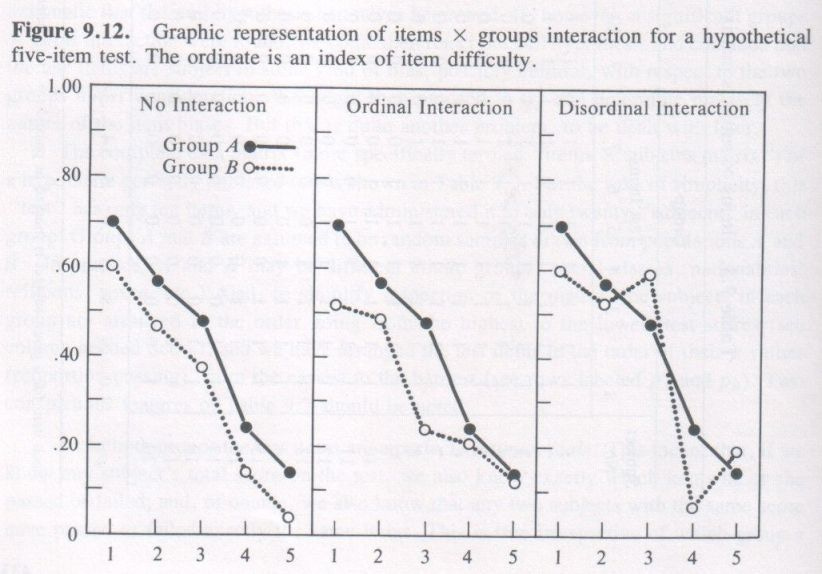
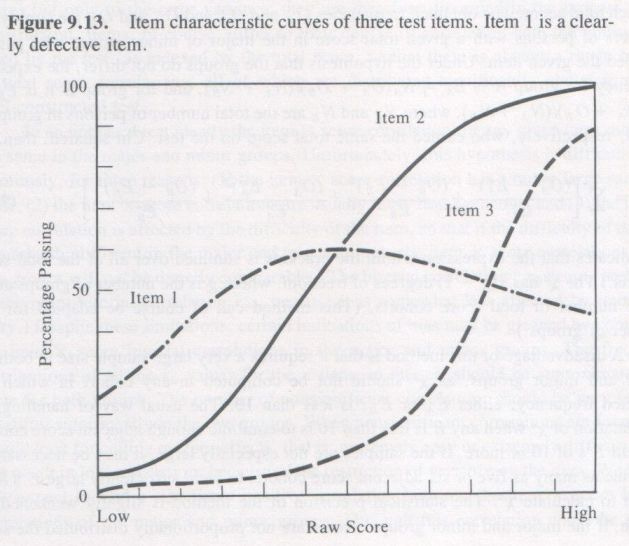
Item x Group Interaction
Ch.12 External Sources of Bias

Chapter 6 Do IQ Tests Really Measure Intelligence?

Causes of Correlation

Textbooks constantly remind us that correlation does not necessarily imply causation. Two variables with no direct causal connection between them may be highly correlated as a result of their both being correlated (causally or not) with a third variable. Even if rxy = 0, we cannot be sure there is no causal connection between x and y. A causal correlation between x and y could be statistically suppressed or obscured because of a negative correlation of x with a third variable that is positively correlated with y. A variable that, through negative correlation with x (or y) and a positive correlation with y (or x), reduces the correlation rxy is called a suppressor variable.

To establish causality, other information than correlation is needed. Temporal order of the correlated variables increases the likelihood of causality, that is, if variable x precedes variable y in time, it is more likely that x causes y. But even correlation plus temporal order of the variables is insufficient as a proof of causality. To prove causality we must resort to a true experiment, which means that the experimenter (rather than natural circumstances) must randomly vary x and observe the correlated effect on y. If random experimental manipulation (i.e., experimenter-controlled variation) of variable x is followed by correlated changes in y, we can say that variation in x is a cause of variation in y. This is why experimental methods are so much more powerful than correlation alone. Unfortunately, much of the raw material found in nature that we wish to subject to scientific study cannot be experimentally manipulated - to do so may be practically unfeasible or it may be morally objectionable. It is largely for these reasons that experimental plant and animal genetics have been able to make much greater scientific strides than human genetics.

Although it is a commonplace truism that “correlation does not prove causation,’’ one seldom sees any discussion of the causes of correlation between psychological variables. [...]

1. Common Sensory-Motor Skill. Variables x and y may be correlated because they involve the same sensory-motor capacities. This is a practically negligible cause of correlation among most tests of mental ability. That is, very little, if any, of the test variance in the normative population is attributable to individual differences in visual or auditory acuity or to motor coordination, physical strength, or agility. Persons with severe sensory or motor handicaps must, of course, be tested for mental ability on specially made or carefully selected tests on which performance does not depend on the particular sensory or motor function that is disabled.

2. Part-Whole Relationship. Variables x and y may be correlated because the skills involved in x are a subset of the skills required in y. For example, x is a test of shifting automobile gears smoothly and y is a driving test; or x is a test of reading comprehension and y is a verbal test of arithmetic problem solving. Transfer of skill from one situation to another, due to common elements, also comes under this heading. Playing the clarinet and playing the saxophone are more highly correlated because of common elements of skill than the correlation between playing the clarinet and playing the violin, which involves fewer elements in common.

3. Functional Relationship. Variables x and y may be functionally related in the sense that one skill is a prerequisite for the other. For example, a performance on a digit-span test of short-term memory may correlate with performance on an auditory test of arithmetic problem solving, because the subject must be able to retain the essential elements of a problem in his memory long enough to solve it. Memory may not be intrinsic to arithmetic ability per se (i.e., it is not a part-whole relationship), as might be shown by a much lower correlation between auditory digit-span and arithmetic problems presented visually so that the person does not have to be able to remember all the elements of the problem while solving it.

4. Environmental Correlation. There may be no part-whole or functional relationship whatever between x and y, and yet there may be a substantial correlation between them because the causes of x and y are correlated in the environment, whether x and y be specific skills or items of knowledge. For example, there is no functional or part-whole connection between knowledge of hockey and knowledge of boxing, yet it is more likely that persons who know something about hockey will also know something more about boxing than they will about say, the opera. And it is more likely that the person who knows something about symphonies will also know something about operas. In all such cases, correlated knowledge is a result of correlated environmental experiences. The same thing applies to skills; we would expect to find a positive correlation between facility in using a hammer and in using a saw, because hammers and saws are more correlated in the environment than are, say, hammers and violins. Different environments and different walks of life can make for quite different correlations among various items of knowledge and specific skills. On the other hand, a common language, highly similar public schools, movies, radio, television or other mass media, and mass production of practically all consumer goods and necessities all create a great deal of common experience for the vast bulk of the population.

5. Genetic Correlation. Variables x and y may be correlated because of common or correlated genetic determinants. There are three kinds of genetic correlation that are empirically distinguishable by the methods of quantitative genetics: correlated genes, pleiotropy, and genetic linkage.

Correlated genes, through selection and assortative mating - segregating genes that are involved in two (or more) different traits, may become correlated in the offspring of mated pairs of individuals both of whom carry the genes of one or the other of the traits. For example, there may be no correlation at all between height and number of fingerprint ridges. Each is determined by different genes. But, if, say, tall men mated only with women having a large number of fingerprint ridges, and short men only with women having few ridges, in the next generation there would be a positive genetic correlation between height and fingerprint ridges. Tall men and women would tend to have many ridges and short persons would have few. Breeding could just as well have created a negative correlation or could wipe out a genetic correlation that already exists in the population. A genetic correlation may also coincide with a functional correlation, but it need not. Selective breeding in experimental animal genetics can breed in or breed out correlations among certain traits. In the course of evolution, natural selection has undoubtedly bred in genetic correlations among certain characteristics. Populations with different past selection pressures and different factors affecting assortative mating, and consequently different evolutionary histories, might be expected to show somewhat different intercorrelations among various characteristics, behavioral as well as physical.

Pleiotropy is the phenomenon of a single gene having two or more distinctive phenotypic effects. For example, there is a single recessive gene that causes one form of severe mental retardation (phenylketonuria); this gene also causes light pigmentation of hair and skin, so that the afflicted children are usually more fair complexioned than the other members of the family. Thus, there is a pleiotropic correlation between IQ and complexion within these families.

Genetic linkage causes correlation between traits because the genes for the two traits are located on the same chromosome. (Humans have twenty-three pairs of chromosomes, each one carrying thousands of genes.) The closer together that the genes are located on the same chromosome, the more likely are the chances of their being linked and being passed on together from generation to generation. Simple genetic correlation due to selection can be distinguished from correlation due to linkage by the fact that two traits that are correlated in the population but are not correlated within families are not due to linkage. Linkage shows up as a correlation between traits within families. (In this respect it is like pleiotropy.)

Influences on Obtained Correlations

It is also important to understand that obtained correlations in any particular situation are not Platonic essences. They are affected by a number of things. Suppose that we are considering the correlation between two variables, x and y. We give tests X and Y to a group of persons and compute rxy. Now we have to think of several things that determine this particular value of rxy:

1. First, there is the correlation between X and Y in the whole population from which our group is just a sample. The correlation in the population is designated by the Greek letter rho, pxy. Obviously the larger our sample, the closer rxy is likely to come to pxy. Any discrepancy between rxy and pxy is called sampling error and is measured by the standard error of the correlation, SEr (not to be confused with the standard error of estimate). SEr = (1-r²)/SQRT(N-1), where N is the number of persons (or pairs of correlated measurements) in the sample. (When p is zero, SEr = 1/SQRT(N-1).) The sample size does not affect the magnitude of the correlation, but only its accuracy, and SEr is a measure of the degree of accuracy with which the correlation coefficient r obtained from a sample estimates the correlation p in the population. So we should always think of any obtained correlation as r ± SEr; that is, r is a region, a probabilistic estimate that tells us that r is most likely in the region of +1 SEr to -1SEr from the population correlation p. The expression r = .55 ± .03, for example, means that .55 most likely (i.e., more than two chances out of three) falls within the range of plus or minus .03 of p; or, to put it another way, that p most probably lies somewhere between .52 and .58. The larger the sample, the smaller is SEr and the more accurate is r as an estimate of p. We are usually more interested in r as an estimate of p than in the sample r for its own sake.

2. The so-called range of talent in one or both variables also affects the correlation. This is an important factor to consider in making inferences from the sample r to the population p, because generally the range of talent in the samples used in most research studies is considerably more restricted than the range of talent in the general population. Restriction of range in either variable (or both) lowers the correlation. For example, the correlation between height and weight in the general population is between 0.6 and 0.7. But, if we determine the correlation between height and weight among a team of professional basketball players, the correlation will drop to between 0.1 and 0.2. The full variation in height and weight found in the general population is not found in the basketball team, all of whom are tall and lean. Figure 6.7 illustrates the effect of restriction of range on the correlation scatter diagram. The moral is that in viewing any correlation, and particularly discrepancies between correlations of the same two variables obtained in different samples, we should consider the range (or variance) of the variables in the particular group in which the correlation was obtained. For example, correlations among ability tests are usually much lower in a college sample than in a high school sample, because the college population has a much more restricted range of intellectual ability - practically the entire lower half of the general population is excluded. Thus the more selective the college, the less will students’ scores on the entrance exam (or other tests of mental ability) correlate with the students’ grade-point averages.

3. The reliability of the tests or measurements affects the correlation. The upper theoretical limit of the correlation between any two measures, say, X and Y, is the square root of the product of their reliabilities, i.e., the maximum possible rxy = SQRTrxxryy, where rxx and ryy are the reliability coefficients of X and Y, respectively. The test's reliability can be thought of as the test's correlation with itself. [7] If we wish to know what our obtained correlation rxy would be if our measures were perfectly reliable, we can make a correction for attenuation. The corrected correlation, rc = rxy/SQRTrxxryy. [...]

A Realistic Example of Factor Analysis

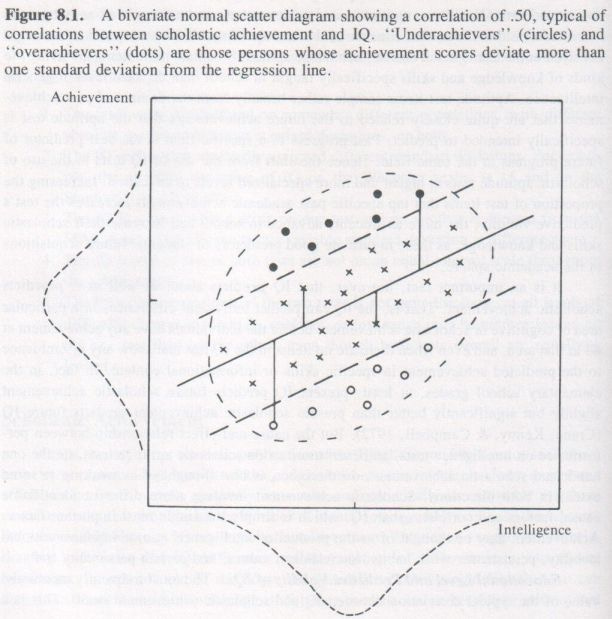
Table 6.5 shows correlations among ten physical and athletic tests. The labels of the tests are all quite self-explanatory, except possibly for variables 7 and 8. In no. 7 the person is required to trace a drawing of a five-pointed star while observing his own performance in a mirror. In no. 8 the person must try to keep a stylus on a small metal disc, called the “target,” about the size of a nickel, while it rotates on a larger hard rubber disc like a phonograph turntable at about one revolution per second. Electrical contact of the stylus with the small metal disc operates a timing device that records the number of seconds per minute that the stylus is in contact with the target.

Inspection of the correlation matrix in Table 6.5 shows that it is not random - there are too many high correlations, all positive, and the large correlations can be seen to be grouped or clustered in different parts of the matrix. The fact that all the r's are positive indicates that there is a substantial general factor in this matrix, and the clustering of high correlations suggests that there are probably also one or more group factors in addition to the general factor.

Table 6.6 shows the first four principal components extracted from the correlation matrix in Table 6.5. Only four components were extracted. Together they account for 89.1 percent of the total variance in the ten variables. The remaining six components, if extracted, would account for only 10.9 percent of the total variance, averaging about 1.8 percent of the variance for each component. Thus none of the six remaining components is retained, as each one accounts for so little as not to be needed to recreate the original correlation matrix, which can be recreated, within the margin of sampling error, using only the first four components. Thus, in a sense, we have reduced ten intercorrelated variables to only four independent factors. The communality, h², indicates the proportion of variance in each variable that is accounted for by the four components. All the communalities are quite large, the smallest being .73. [...]

The first principal component, I, is the general factor, and the main question is, how large is this general factor, that is, how much of the variance does it account for? In this case it accounts for 41.1 percent of the total variance or 46 percent of the total communality. Thus it is a quite large general factor, almost twice as large as the next largest factor, which accounts for only 21.6 percent of the variance. Only two of the tests have relatively small loadings on the general factor - no. 6 (one-leg balance) and no. 7 (mirror star tracing). The best single test of the g factor in this battery is the 100-yard dash, with a g loading of .86. The remaining tests are all pretty much alike in their g loadings.

The second principal component, II, we see, has some large negative as well as large positive loadings; it is therefore called a bipolar factor. What this means is that, when persons are equated on g, those who score high on the tests at one end of the bipolar factor will score low on the tests at the other end. The bipolar factor thus can be interpreted as two factors that are negatively correlated with each other. The high negative loadings on II are handgrip (-.70) and chinning (-.70), followed by a softball throw (-.45). This pole of factor II obviously involves hand-and-arm strength - it might be labeled “upper-limb strength.” The positive pole is less distinct, with largest loadings on pursuit rotor, 1-mile run, and 5-mile run/walk. This is hard to decipher or to label, as these three tests appear so dissimilar. It is hard to imagine why they go together and we can only speculate at this point. The best speculation is that all involve resistance to fatigue of the leg muscles. The short-distance running tests have negligible loadings on this factor. Pursuit rotor tracking is performed standing up, and persons commonly report feeling some fatigue of their leg muscles after working 10 minutes or so at the pursuit rotor. We could experimentally test this hypothesis by giving the pursuit rotor to persons sitting down. Under this condition pursuit rotor performance should have a negligible loading on factor II, if our hypothesis is correct that the positive pole of factor II represents resistance to leg fatigue. This is how factor analysis can suggest experimentally testable hypotheses about the nature of abilities.

Factor III has its largest positive loadings on mirror star tracing (+.80) and pursuit tracking (+.47). It might be labeled “hand-eye coordination,” as that is what these two tests seem to have in common. The long-distance running tests are negatively loaded on this factor, and the other tests have practically negligible loadings.

Factor IV has its largest loading on one-leg balance (+.73) and is also positively loaded on softball throw (+.42), which suggests that it is a body balance factor. It is not a very important factor for most of the tests (accounting for only 12 percent of the total variance).

In any one such analysis our labeling of the factors must always be regarded as speculative and tentative. By repeating such analyses on various groups of subjects, and by including other tests that we hypothesize might be good measures of one factor or another, we can gradually clarify and confirm the nature of the basic factors underlying a large variety of athletic skills. In this particular analysis, we might tentatively summarize the factors as follows:

Factor I General athletic ability.
Factor II Bipolar: Hand-and-arm strength versus resistance to fatigue of leg muscles.
Factor III Hand-eye coordination or fine-motor dexterity.
Factor IV Body balance.

In labeling the first factor “general athletic ability,” we run the risk of overgeneralization if our battery of tests contains only a limited sample of athletic skills. For example, there are no jumping tests; no aiming tests, such as throwing a ball at a target or “making baskets” as in basketball; no dodging obstacles while running, as would be involved in football; and so on. Thus, the general factor derived just from this battery of only ten tests is probably an overly narrow general factor as compared, say, with the general factor extracted from a correlation matrix of twenty different athletic skills. The more different tests we can put into our original correlation matrix, the more sure we can be of the generality of the “general factor” or first principal component. We would most likely find that certain of our tests always have high g loadings regardless of the other tests in the battery, so long as there were a reasonable number and diversity of tests. These tests of more or less consistently high g loadings would therefore be regarded as good indices of g. The best measure of g, of course, would be factor scores based on the g loadings of a large and diverse battery of tests. Essentially, these factor scores are a weighted average of the standardized scores on each of the tests, the weights being proportional to each test’s loading on the general factor. (Factor scores on the other factors are obtained by a different algorithm.) Thus, in terms of our example in Table 6.6, a person who is exactly one standard deviation above the mean on each of the ten tests would have a factor score on the general factor of 0.62 (i.e., the average of the products of the factor loading on each test times the person’s test score in standard deviation units). The unweighted average of the test scores provides only a rough approximation to the general factor, “contaminated” by other factors to the extent that the various tests are not loaded on the general factor.

Because our four factors account for most of the variance in all ten tests, we could more efficiently describe the abilities of each person in terms of four factor scores instead of ten test scores. Even if we added ten more tests, we may still have only five or six (or even four) factor scores. It becomes more and more difficult to add further tests that involve any significant proportion of variance not already accounted for by the several factors involved in all the other tests. Thus factor scores can be a much more efficient means of describing abilities than test scores.

Rotation of Factors. The reader will have noticed that Table 6.6 is labeled “unrotated” factor matrix. This means that the principal components are given just as they emerge from the mathematical analysis, each accounting for the largest possible linear component of variance that is independent of the variance accounted for by all of the preceding components.

Looking back to Figure 6.8 we see two principal components, I and II. We can rotate these axes on their point of intersection, while keeping everything else in place. When rotated into any other position than that shown in Figure 6.8, they are no longer principal components, but rotated factors. The first factor after rotation is no longer a general factor in the sense that it accounts for the maximum amount of variance in all of the tests. Some part, perhaps a large part, of the variance on the first principal component is projected onto the other axes as a result of rotation, depending on the degree of rotation. The total variance remains, of course, unchanged, as all the data points remain fixed in space. Rotation merely changes the reference axes.

Rotation of axes becomes too complex to visualize when there are more than three factors. One would have to imagine four or more straight lines, each one at right angles to each of the others, being rotated around a single point in n-dimensional space!

Why do we bother to rotate the axes? Rotation is often done because it usually clarifies and simplifies the identification, interpretation, and naming of group factors. Other positions of the reference axes may give a more meaningful, practical or intuitive picture. Rotation will not create any new factors that are not already latent in the principal components, but it may permit them to stand out more clearly. It does so, however, at the expense of the general factor (first principal component), the variance of which gets distributed over the rotated factors. Rotation is quite analogous to taking a picture of the same object from a different angle. For example, we may go up in a helicopter and take an aerial photograph of the Grand Canyon, and we can also take a shot from the floor of the canyon, looking through it lengthwise, or from any other angle. There is no one “really correct” view of the Grand Canyon. Each shot better highlights some aspects more than others, and we gain a better impression of the Grand Canyon from several viewpoints than from just any single one. Yet certain views will give a more informative overall picture than others, depending on the particular viewer’s interest. But no matter what the angle from which you photograph the Grand Canyon, you cannot make it look like the rolling hills of Devonshire, or Victoria Falls, or the Himalayas. Changing the angle of viewing does not create something that is not already there; it may merely expose it more clearly, although at the expense of perhaps obscuring some other feature.

In the early days of the development of factor analysis, theorists had heated arguments over whether factors should be rotated, and, if so, just how they should be rotated. Nowadays, there is little if any real argument over this issue. Deciding whether unrotated factors or various rotations are more or less meaningful than others must be based on criteria outside factor analysis itself. The main justification for rotation is to obtain as clear-cut a picture as possible of the latent factors in the matrix. To achieve this, one should look at both the unrotated and rotated factors.

But into what position should the factors be rotated? Again, there is no sacrosanct rule. The main idea is to rotate the axes into whatever position gives the clearest picture of the factorial structure of all the tests. But obviously we need some notion of what we mean by the “clearest picture.”

Thurstone (1947) proposed a criterion for factor rotation that he named simple structure. He believed that simple structure reveals the psychologically most meaningful picture of the factorial structure of any set of psychological tests. Thurstone’s idea of simple structure has become the most common basis for rotation, the aim being to approximate as closely as possible, for any given matrix, the criterion of simple structure. Simple structure is approximated to the extent that the factors can be simultaneously rotated so as to (1) have as many zero (or nearly zero) loadings on each factor as possible and (2) concentrate as much of the total variance in each test on as few factors as possible. Table 6.7 shows an idealized factor matrix with perfect simple structure. You can see that the interpretation of the factors in terms of the tests they load on is greatly simplified, as is the interpretation of the tests in terms of the factors they measure. Each test represents a single factor. Such tests would be called factor-pure tests because they measure only one factor, uncontaminated by any others. It was Thurstone’s dream to devise such factor-pure tests to measure the seven “Primary Mental Abilities” represented by the seven factors that he succeeded in extracting reliably from multitudes of highly diverse cognitive tests.

The general factor worked against this dream. It pervaded all the tests and thereby made it impossible to do more than approach simple structure; the tests always had substantial loadings on more than one factor, because the rotation spreads the general factor over the several rotated factors, so that simple structure, while it can be more or less approximated, cannot be fully achieved as long as there is a substantial general factor.

To get around this problem, Thurstone adopted the method of oblique factor rotation. When all the rotated axes are kept at right angles to one another, regardless of the final position to which they are all simultaneously rotated, the rotation is termed orthogonal. When simple structure cannot be closely approximated by means of orthogonal rotation (which will always be the case when there is a large general factor), one can come closer to simple structure by letting the factor axes assume oblique angles in relation to one another, rather than maintain all the axes at right angles. The axes and angles, then, are allowed to move around in any way that will most closely approximate simple structure. But recall the fact that, when the angles between axes are different from 90°, that is, when they are oblique angles, the factors are no longer uncorrelated. Oblique rotation makes simple structure possible by making for correlations between the factors themselves. In other words, one gets rid of the general factor in each of the rotated primary factors by converting this general factor variance into covariance (i.e., correlation) among the factors themselves.

Thus the correlations among oblique factors can themselves be subjected to factor analysis, yielding second-order factors, which are of course fewer in number than the primary factors. Usually with cognitive tests only one significant second-order factor emerges - the general factor. If there are two or more second-order factors, they too can be obliquely rotated and their intercorrelations factor analyzed to yield third-order factors. At some point in this process there will be just one significant factor - the general factor - at the top of the hierarchical factor structure, as pictured in Figure 6.9. The general factor will show up as the first unrotated factor, or as the highest factor in a hierarchical analysis of rotated oblique factors, as shown in Figure 6.9. One can arrive at essentially the same g factor from either direction. It is seldom a question of whether there is or is not a g factor, but of how large it is in terms of the proportion of the total variance it accounts for.

Now let us see what orthogonal rotation to approximate simple structure does to our matrix of physical variables. Table 6.8 shows the rotated factors for the physical ability measures. An objective mathematical criterion of simple structure was used, called varimax, because it rotates the factors until the variance of the squared loadings on each factor is maximized (Kaiser, 1958). Obviously the variance of the squared loadings on any given factor will be maximized when the factor loadings approach either 1 or 0. The method (now usually done by computer) rotates all the factors until a position is found that simultaneously maximizes all the variances of the squared loadings on each factor, that is, produces as many very large and very small loadings as the data will allow.

We could obtain an even closer and more clean-cut approximation to simple structure had we allowed oblique factors in our rotation. But obliqueness also introduces greater sampling error, and we therefore have less confidence in the stability of our results than if we maintained orthogonality.

The rotated factors in Table 6.8 are quite clear. The general factor has been submerged in the rotated factors. Notice that the communalities, h², remain unchanged and that the four factors account for 89.1 percent of the variance but that each factor now accounts for a more equal share of the total variance than was the case with the unrotated factors. The general factor, which had carried so much of the variance (41.1 percent), is now spread out and submerged within the four “simple structure” factors. The rotated factors, just like the unrotated principal components, will reproduce, to the same degree of approximation, all the correlations in the original matrix, by applying the same rule that the correlation between any two variables is the sum of the products of their loadings on each of the factors.

Factor I, with very large loadings on the first three tests, is clearly a “hand-and-arm strength” factor. (It is the same factor that we identified as one pole of the bipolar factor II in the unrotated factor matrix; see Table 6.6.)

Factor II, with its largest loadings on variables 9 and 10, and also a moderately large loading on variable 5, is a running or leg strength factor, and suggests resistance to fatigue of leg muscles, as it is most heavily loaded on the most arduous and fatiguing running tasks. In fact, it could even be a general resistance to fatigue or a general endurance factor. (It is essentially the same factor as one pole of bipolar factor II in the unrotated matrix.)

Factor III, with its only large loadings on mirror star tracing and pursuit rotor tracking, is clearly a hand-eye coordination or fine muscle dexterity factor. (It is the same as factor III in the unrotated matrix.)

Factor IV has its only large loading on one-leg balance and is thus a body balance factor, the same as factor IV in the unrotated matrix.

Intelligence and Achievement

In a series of large statistical analyses, too complex to be explicated here in detail, William D. Crano has attempted to determine the direction of causality between intelligence and achievement (Crano, et al., 1972; Crano, 1974). The investigation used a technique known as cross-lagged correlation analysis. In brief, intelligence tests and a variety of scholastic achievement tests were given to large samples of school children in Grade 4 and two years later in Grade 6. The key question is, Do the Grade 4 achievement tests predict Grade 6 IQ more or less than Grade 4 IQ tests predict Grade 6 achievement? If the correlation from Grade 4 to 6 is higher in the direction IQ4 → Achievement6 than in the direction Achievement4 → IQ6, it can be reasonably argued that individual differences in IQ have a causal effect on individual differences in achievement. This, in fact, is what was found for the total sample of 5,495 pupils. However, when the total sample was broken down into two groups consisting of pupils in suburban schools and pupils in inner-city schools (in other words, middle- and lower-socioeconomic-status groups), the cross-lagged correlations showed different results for the two groups. The suburban group clearly showed the causal sequence IQ4 → Achievement at a high level of statistical significance, whereas the results of the inner-city group were less clear, but suggested, if anything, the opposite causal sequence, that is, Achievement4 → IQ6, at least for verbal IQ. (The Ach4 → Nonverbal IQ6 was significant only for arithmetic achievement.) Also a high-IQ sample (one standard deviation above the mean) showed a much more prominent IQ4 → Ach6 cause-effect correlation than did a low-IQ sample (one standard deviation below the mean). The predominant direction of causality is from the more abstract and g-loaded tests to the more specific and concrete skills. For example, in the total sample and in both social-class groups, Verbal IQ in Grade 4 predicts spelling in Grade 6 significantly higher than spelling in Grade 4 predicts Verbal IQ in Grade 6.

Factor analysis has shown that the Verbal IQ of the Lorge-Thorndike Intelligence Test used in Crano’s study measures mainly crystalized intelligence gc, whereas the Nonverbal IQ is mainly fluid ability g, (Jensen, 1973d). Consistent with Cattell’s theory of gf and gc, Crano et al. (1972) found that Grade 4 Nonverbal IQ (gf) predicts Grade 6 Verbal IQ (gc) more highly than Grade 4 Verbal IQ predicts Grade 6 Nonverbal IQ, and this is true in both social-class groups. Thus, gf can be said to cause gc more than the reverse. Crano et al. (1972, p. 272) conclude as follows:

The findings indicate that an abstract-to-concrete causal sequence of cognitive acquisition predominates among suburban school children. The positive and often statistically significant cross-lagged correlation values . . . also indicate that the concrete skills act as causal determinants of abstract skills; their causal effectiveness, however, is not as great as that of the more abstract abilities. Taken together, these results suggest that the more complex abstract abilities depend upon the acquisition of a number of diverse, concrete skills, but these concrete acquisitions, taken independently, do not operate causally to form more abstract, complex abilities. Apparently, the integration of a number of such skills is a necessary precondition to the generation of higher order abstract rules or schema. Such schema, in turn, operate as causal determinants in the acquisition of later concrete skills, (italics added)

Chapter 7 Reliability and Stability of Mental Measurements

Conditions That Influence Test Reliability

Scoring. The scoring of many of the items in individually administered intelligence tests, such as the Stanford-Binet and the Wechsler scales, requires a subjective judgment on the part of the tester as to whether the examinee passed or failed the item. For example, in the vocabulary test the tester has to decide whether the definitions given by the examinee are to be scored right or wrong. (In the Wechsler tests the answer to each vocabulary item is scored 2, 1, or 0, depending on the quality of the examinee’s response.) To the extent that testers do not agree on the scoring of a given response, the reliability of the total score is lowered. To keep the scoring reliability (i.e., agreement among testers) as high as possible, the scoring instructions are made quite explicit in the test manual, with many examples of passing and failing responses to each item. Moreover, the standard for passing any given item is made very lenient, so that a failing response is quite easily agreed on. Doubtful and ambiguous “correct” responses are generally scored as correct, so there will be high agreement among different scorers as to which answers are clearly wrong. (The Stanford-Binet scoring criteria are more lenient in this respect than the Wechsler’s.)

Besides having explicit scoring criteria, individually administered tests should be given and scored only by trained persons. An essential part of such training consists of supervision and criticism of the trainee’s performance in ways that make the procedures of testing and scoring more uniform and standardized and hence more reliable. With such training the agreement among scorers can be made very high, with interscorer correlations in the high .90s. Less than perfect agreement among scorers will be reflected in the test’s reliability coefficient. If the test’s reliability is adequately high for one’s purpose, it follows that the reliability of the scoring itself is satisfactory, as the scoring reliability cannot be less than the test’s internal consistency reliability.

It is commonly believed that, by uniformly relaxing the administration procedures or scoring criteria for all testees, the less able will enjoy an advantage. That is, everyone’s score would rise, but the low scorers would rise relatively more under more lenient conditions. When this has been tried, the brighter testees benefit most in absolute score, but the rank order of subjects is hardly changed. Little and Bailey (1972), for example, gave the WAIS Comprehension and Similarities subtests to college students under conditions that would maximize their performance, by urging the students to give all the correct answers they could think of to each question, without time limit. Scores were obtained by giving credit for all correct answers on each item, as contrasted with the standard WAIS scoring procedure of giving a maximum of two points to each item. The result of the more “generous” procedure was to spread the higher- and lower-scoring students farther apart, while the “generous” and standard scores correlated very highly (r = .93 for Comprehension, .84 for Similarities). This shows that even when the conditions of administration and scoring are altered quite drastically, provided that it is done uniformly for all testees, the rank order of persons’ scores is little changed. There is little statistical interaction of testees and scoring procedures. Thus the scoring criteria themselves, if uniformly applied, are not a potent influence on test reliability.

The same thing is usually true of allowing unlimited time on normally timed tests. The untimed condition will result in higher scores, but the correlation between the timed and untimed scores will be very high. Persons’ scores on a power test maintain much the same rank order for various time limits, provided that the time limit is the same for everyone. A power test is one in which the items are arranged in order of increasing difficulty, and the time limit is such that most testees run out of ability, so to speak, before they run out of time, so that increasing the time limit has little effect on the score. Most tests of intelligence and achievement are power tests. In contrast, speed tests are comprised of many easy items all of which nearly everyone would answer correctly if there were no time limit. Tests of clerical and motor skills are commonly of this type.

Most group-administered tests have completely objective scoring, so there is no question of scoring reliability, barring clerical inaccuracies due to carelessness or to defects in the equipment in the case of machine-scored tests. Such clerical errors are generally rare, and precautions can be taken to reduce their occurrence, such as by having every test scored independently by two persons (or machines) and checking disagreements.

Standardized tests administered and scored by classroom teachers who are untrained and unsupervised in their testing procedures can yield highly unreliable and invalid scores. It is not the rule, fortunately. But we have found numerous deplorable instances in our retesting of teacher-tested classes, on the same tests, by trained testers, under very careful standardized conditions. Some of the teacher-administered test results were found highly discrepant, usually due to incomplete or improper test instructions, lax observance of time limits on timed tests, and a poor testing atmosphere resulting from a disorderly class. Tests administered under such conditions are useless, at best. (This problem is discussed more fully in Chapter 15, pp. 717-718.)

Guessing. Most objective tests are of the multiple-choice type, in which the testee must select the one correct answer from among a number of incorrect alternatives called distractors. The testee who does not know the correct answer to a given item may leave it unanswered or may make a guess, with some chance of picking the correct answer. When there are many difficult items, there is apt to be more guessing. A corollary of this is that persons with lower scores are more likely to guess on more items, as there are fewer items to which they know the answers.

Guessing lowers the reliability of test scores, because items that are gotten right merely by chance cannot represent true scores. “Luck” in test taking is simply a part of the error variance or unreliability of the test. The larger the number of multiple-choice alternatives, the smaller the chances of guessing the correct answers, and, consequently, the less damage to the reliability of the test. True-false items are in this respect the worst, as there is a 50 percent chance of being right by guessing. Recall tests are the best, as no alternatives are given and the testee must produce his own answer. (This is the case in most individual tests of intelligence.) A study by Ruch (cited by Symonds, 1928) illustrates the effect of the number of multiple-choice response alternatives on the reliability of equivalent tests of one hundred items:

Type of Answer                              Reliability Coefficient
Recall                                                             .950
7-alternative multiple choice                     .907
5-altemative multiple choice                     .882
3-altemative multiple choice                     .890
2-alternative multiple choice                     .843
True-false                                                      .837

Test constructors have devised complex ways of scoring tests, taking account of right, wrong, and unanswered items and the number of multiple choice alternatives, so as to minimize the effects of guessing on the total scores and on their reliability. [4] Most modem standardized tests take account of these factors in their scoring procedures, and their reliabilities can be high despite persons’ tendency to guess when they are unsure of the right answer.

Range of Ability in the Sample. Reliability is not a characteristic of just the test, but is a joint function of the test and the group of persons to which it is given. A test with high reliability in one group may have much lower reliability in a different group.

The principal condition that causes variations in a test’s reliability from one group to another is the range of test-relevant ability in the group. A test administered to a group that is very homogeneous in the ability measured by the test will have lower reliability in that group than the same test administered to a more heterogeneous group.

Any decrease in the range of obtained scores or any piling up of scores in one part of the scale automatically lowers reliability. Piling up of scores occurs when a test is too difficult or too easy for a given group, or when persons at the upper and lower extremes of ability have been excluded. (The most dependable index of the score dispersion in a group is the standard deviation, because it takes all the scores into account, not just the most extreme values, which define the range.)

Tests have their maximum reliability when the average item difficulty is 50 percent passing. In this case, the frequency distribution of the total scores will be symmetrical about the group mean.

Another way of saying all this is that to have maximum reliability a test must tap the full range of ability in the group. Otherwise the test is said to have a ceiling effect or a floor effect that results in inadequate discriminatory power at the high or low ends of the scale.

Miscellaneous Sources of Unreliability. Of the numerous other factors that can reduce a test’s reliability, the most often recognized are

1. Interdependence of items lowers reliability; that is, the answer to one item is suggested in another, or knowing the answer to one item presupposes knowing the answer to another item. The effect on reliability is like that of reducing the number of items in the test.

2. Dissimilarity in the experiential backgrounds of persons taking the test can lower reliability. Conversely, tests that sample the more common elements of experience are more reliable. Thus tests of knowledge and skills acquired in school are likely to be more reliable than tests of knowledge and skills acquired in the home, other parameters of the tests being equal.

3. For reasons related to factor 2, scholastic achievement tests administered late in the school year tend to have higher reliability than those given at the beginning of the year.

4. “Tricky” questions or “catch” questions lower the reliability of a test.

5. Wording of test items - words that are overemphasized and may mislead, emotionally toned words that distract from the main content, overly long wording of the question, strange and unusual words, poor sentence structure and unusual word order - all these features lower the reliability.

6. Inadequate or faulty directions or failure to provide suitable illustrations of the task requirements can lower reliability. Giving several easy practice items at the beginning of the test can increase reliability.

7. Accidental factors such as breaking a pencil or interruptions and distractions lower reliability, especially in timed tests.

8. Subject variables such as lack of effort, carelessness, anxiety, excitement, illness, fatigue, and the like may adversely influence reliability.

Regression toward Which Mean ? ... The net effect of using such estimated true scores, besides increasing the accuracy of measurement, is to reduce the higher scores of persons belonging to low-scoring subgroups and boost the lower scores of persons belonging to high-scoring subgroups. Such an outcome may seem unfair from the standpoint of members of the lower-scoring subgroups, but it is merely the statistically inevitable effect of increasing the accuracy of measurement. When higher scores are preferred in the selection procedure, the “luck” factor resulting from unreliability statistically favors persons belonging to lower-scoring groups. The “luck” factor is minimized by using estimated true scores instead of obtained scores.

Causes of Score Instability

Measurement Error Per Se. These are the same factors that lower the reliability, mentioned earlier, and can show up as score instability with test-retest intervals of less than a week. They involve scoring errors, variability in the testing situation itself, and short-term fluctuations in the testee’s attentiveness, willingness, emotional state, health, and the like. All these influences on stability are quite minor contributors to the long-term test-retest instability of test scores, however, as indicated by the very high stability coefficients for short test-retest intervals, which scarcely differ from the reliability coefficients based on a single administration of the test.

Practice Effects. Gaining familiarity with taking tests results in higher scores, usually of some 3 to 6 IQ points - more if the same test is repeated, less if a parallel form is used, and still less if the subsequent test is altogether different. Practice effects are most pronounced in younger children and persons who have had no previous experience with tests. In a minority of such cases retest scores show dramatic improvements equivalent to 10 or more IQ points. The reliability and stability of scores can be substantially improved by giving one or two practice tests prior to the actual test on which the scores are to be used. The effects of practice in test taking rapidly diminish with successive tests and are typically of negligible consequence for most school children beyond the third grade unless they have had no previous exposure to standardized tests.

Because nearly all persons show similar effects of practice on tests, practice has little effect on the ranking of subjects’ scores except for those persons whose experience with tests is much less or much greater than for the majority of the persons who were tested. [...]

Individual Differences in Rate of Maturation. Even when all of the other causes of score instability are accounted for, some fluctuation in scores still remains, however, becoming less and less as children approach maturity. These fluctuations are due to intrinsic individual differences in rate of development. They are apparent in physical as well as in mental growth. Growth of any kind does not proceed at a constant rate for all individuals, there are spurts and lags at different periods in each person’s development. These, of course, contribute to lower stability coefficients of scores over longer intervals. Figure 7.3 shows individual mental growth curves from 1 month to 25 years for five boys. One clearly sees both stability and instability of the mental growth rates in these graphs.

Spurts and lags in the rate of mental development are conditioned in part by genetic factors, as indicated by the fact that the pattern of spurts and lags in mental development scores, at least in the first two years, coincides more closely for identical than for fraternal twins (Wilson, 1972). On the other hand, the constant aspect of mental growth rates appears to be much more genetically determined than the pattern of lags and spurts, which evidently reflects changing environmental influences to a considerable extent (McCall 1970).

Changes in Factor Composition. The very same test items cannot be used over very long test-retest intervals during childhood. Items that discriminate at ages 2 to 4 are much too easy and therefore nondiscriminatory at ages 6 to 8. Consequently, the item composition of tests must necessarily change from year to year over the interval from infancy to adolescence if the tests are to be psychometrically suitable at every age. Changing the items in tests to make them appropriate, reliable, and discriminating for each age may introduce changes in the factor composition of the test, so that the test does not actually measure exactly the same admixture of abilities at every age level. To the extent that the factor composition of the test changes at different age levels, the age-to-age correlations are reduced. Infant tests consisting of items that are appropriate below 2 years of age, for example, measure almost entirely perceptual-motor abilities, attention, alertness, muscular coordination, and the like. There are a few simple verbal commands and some assessment of the quality of the infant’s vocalization, but there are no items that call for abstraction, generalization, reasoning, or problem solving. Such items can be successfully introduced only after about age 2 or 3, and then only in a rudimentary form. Hence, tests before about age 4 or 5 are not as highly g loaded as later tests and are therefore rather poor predictors of scores on the much more g-loaded tests given to school-age children and adults. Below 2 years, scores on infant tests of development correlate negligibly with school-age IQs, and below 1 year of age the scores have zero correlation with IQ at maturity, provided that one excludes infants who are obviously brain damaged or have other gross pathological conditions.

Beyond age 2, however, most of the variance in Stanford-Binet IQs is attributable to the same general factor at every age level, steadily rising from about 60 percent g variance at age 2 to about 90 percent by age 10. The same thing is very likely true also of the Wechsler scales, in which the same types of subtests (though of course different items) are used throughout the age range from 5 years to adult.

Different abilities show varying degrees of stability from age to age. More complex and “higher,” or g-loaded, functions, such as reading, arithmetic, spelling, sentence completion, composition, and the like have been found to be more stable than simpler abilities such as number checking, handwriting, auditory memory span, and the like (Keys, 1928, p. 6). The various subtests of the General Aptitude Test Battery (developed by the U.S. Employment Service) display the typical differences in stability of various abilities, as shown in Table 7.12.

After g, verbal facility and knowledge appear to be the most stable, especially after maturity. The more fluid abilities such as abstract reasoning, problem solving, and memory are somewhat less stable after maturity, showing greater individual differences in rates of decline, especially in adults past middle age. In adults, crystalized abilities, as measured for example by tests of general information and vocabulary, go on gradually increasing up to middle age and often beyond, whereas the fluid abilities (e.g., matrices, block design, figure analogies, and memory span) show a gradual decline with advancing age. Overall ability level on omnibus tests of general intelligence shows little change throughout adulthood until advanced old age, as the gradual decline in fluid abilities is compensated for by the gradual increase in crystalized abilities.

Scale Artifacts. Studies of IQ stability based on age-to-age differences in IQ often show more instability of scores than would be inferred from age-to-age correlations. The explanation is that interage score differences are much more sensitive to imperfect scaling than are interage score correlations. If the units of the IQ scale are not equal from one age to another, a person will show IQ differences when there is really no change at all in his mental status relative to his age peers. The 1916 and 1937 editions of the Stanford-Binet had this scale defect as a result of calculating IQs as the ratio of mental age to chronological age (i.e., IQ = 100 MA/CA). Because this ratio had slightly different standard deviations at different ages, a constant IQ from one age to another could not represent a constant relative status. Conversely, if the person’s relative status remained stable from one year to the next, the IQ would have to change. Such a change is pure artifact due to inequalities in the IQ scale from year to year. This was the main reason for abandoning the ratio IQ and using instead a deviation IQ, which is a standardized score that represents the person’s deviation from his or her age-group mean in standard deviation units. Deviation IQs, which were adopted in the 1960 revision of the Stanford-Binet (as well as in all of the Wechsler tests and virtually all modern group tests of intelligence), maintain the same relative status from one age to another. The end result of changing from ratio IQs to deviation IQs is to reduce the age-to-age difference in IQ, although the age-to-age correlations remain the same. For example, an analysis of Stanford-Binet IQ changes in forty-two children between 6 and 12 years of age showed an average absolute change of 12.9 points for ratio IQs but only 9.8 points for deviation IQs (Pinneau, 1961).

An implication of using deviation IQs, which is too often forgotten, is that they cannot be used to compute mental age from the formula MA = CA X IQ/100. (The 1960 Stanford-Binet Manual, Part III, presents a table of the correct conversions from MA to IQ and vice versa.)

Chapter 8 Validity and Correlates of Mental Tests

Concurrent Validity of IQ Tests. How well do scores on different IQ tests agree with one another? Do different IQ tests measure one and the same intelligence? [...]

It can be seen that the correlations range widely, with an overall mean of +.67. Many studies have been summarized in terms of the total range of correlations (i.e., the lowest and highest r’s that are found in any of the studies) and the median value of the entire set of correlations (indicated in parentheses in Table 8.5). The mean of the median values is +.77. The mean of all the lower values of the range of correlations is +.50, and the mean of all the higher values of the range is +.82. Thus the correlations among various IQ tests can be said to be most typically in the range from about +.67 to +.77. The lower limit of the range of correlations between certain tests is often the result of studies based on small samples or on atypical groups, such as retardates, psychiatric patients, college students, or other groups with a restricted range of scores. Correlations are generally higher in studies based on representative samples of the general population. Also, some of the tests showing the lowest correlations with other tests (e.g., “Draw-a-Man and the Quick Test”) may be questioned as measures of intelligence even on the basis of other psychometric criteria than their poor correlations with a quite good test of intelligence such as the WISC.

Correlations between IQ tests in the range from .67 to .77 are just about what one should expect if the g loadings of most IQ tests range from .80 to .90 and the tests have little variance other than g in common. The reader may recall from Chapter 6 that the correlation between any two tests can be expressed as the sum of the products of the tests’ loadings on each of the common factors. By far the largest common factor in IQ tests is g. Tests with g loadings in the .80 to .90 range, therefore, would show intercorrelations ranging from .64 to .81. Other common factors, such as verbal ability, would tend to raise the correlations only slightly. The fact that the median correlation between the Wechsler Intelligence Scale for Children and the Stanford-Binet in forty-seven studies is .80 suggests that these two tests have g loadings of close to .90 (i.e., √.80), which is only slightly less than the reliabilities of these tests (i.e., about .95).

It should be remembered that the correlation between tests indicates mainly the degree to which persons maintain the same relative standing on the various tests. A high correlation does not guarantee that the IQ scores themselves will be alike on every test. It is often noticed that even though individuals remain in very much the same rank order on two different IQ tests, meaning there is a high correlation between the tests, the actual IQ scores may be quite discrepant on the two tests. The discrepancies in the two IQs may show up consistently throughout the whole range, or they may differ in direction and magnitude in the lower, middle, and upper ranges of the IQ scale. Hence the various IQ scales themselves, although they may be highly correlated, are not exactly equivalent in an absolute sense. In this respect mental testing is currently in the situation similar to the measurement of distance and weight before the adoption of uniform international standards of measurement. [...]

The most common causes of the IQ scale discrepancies among various intelligence tests are the following:

1. The tests were standardized on somewhat different populations, with different absolute means or different standard deviations, or both. 2. The IQ scales were arbitrarily assigned different standard deviations. For example, the standard deviation of IQ on the Wechsler scales is 15 and on the Stanford-Binet it is 16. 3. The IQ is a standardized score on one test and on another is derived from the MA/CA ratio (which results in a variable standard deviation at different ages). 4. The IQ scores of one or both tests are not on an equal-interval scale throughout the whole range. 5. The factorial composition of the two tests is not quite the same, at all levels of difficulty. Scores in the high, medium, or low range may be more g loaded on the one test than on the other, even though both tests overall are equally g loaded.

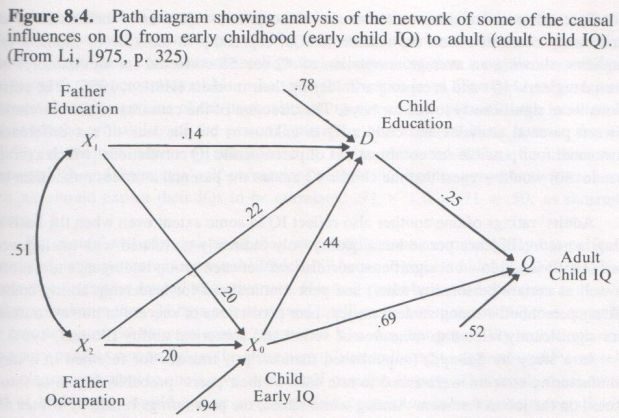
IQ not a Threshold Variable for Scholastic Achievement. Note that the regression line of achievement on intelligence in Figure 8.1 is linear throughout the entire range of IQ scale. This is typical of the findings of the many studies that have investigated the form of the regression of achievement on IQ. ... There is no point on the IQ scale below which or above which IQ is not positively related to achievement. This means that IQ does not act as a threshold variable with respect to scholastic achievement, as has been suggested by some of the critics of IQ tests ... The evidence is overwhelming that scholastic achievement increases linearly as a function of IQ throughout the entire range of the IQ scale so long as scholastic achievement itself is measured on a continuous scale unrestricted by the artifacts of ceiling or floor effects due to the achievement tests not including simple enough or advanced enough items.

Achievement in Elementary School. Results quite typical of those found in most studies of the predictive validity of IQ are seen in a large-scale study by Crano, Kenny, and Campbell (1972). It has the added advantage of showing both the concurrent and predictive validities of IQ. Achievement was measured by a composite score on the Iowa Tests of Basic Skills, which measure achievement and skills in reading, language (spelling, punctuation, usage, etc.), arithmetic, reading of maps, graphs, and tables, and knowledge and use of reference materials. IQ was measured by the Lorge-Thorndike Intelligence Test. The tests were taken by a representative sample of 5,495 children in the Milwaukee Public Schools in Grade 4 and parallel forms of the tests were obtained again in Grade 6. Figure 8.2 shows all of the correlations among the four sets of measurements. Notice that the predictive validity of IQ over an interval of two years (IQ4-Ach6) is nearly as high as the concurrent validity (IQ4-Ach4 and IQ6-Ach6). As is typically found, past achievement predicts future achievement slightly better than IQ.

One might wonder to what extent the common factor of reading ability per se involved in group tests of IQ and achievement plays a part in such intercorrelations. It is not as great as one might imagine. Although the verbal items of group IQ tests usually involve reading, the reading level is deliberately made simpler than the conceptual demands of the items, so that individual differences in the IQ scores are more the result of general cognitive ability than of reading ability per se. The reading requirements of an IQ test for sixth-graders, for example, will typically involve a level of reading ability within the capability of the majority of fourth-graders. The Lorge-Thorndike IQ test has both Verbal and Nonverbal parts; the Verbal requires reading, the Nonverbal does not. In a large study (Jensen, 1974b) of children in Grades 4 to 6, a correlation of .70 was found between the Verbal and Nonverbal IQs. The correlation between Verbal IQ and the reading comprehension subtest of the Stanford Achievement Test was .52. The correlation between Nonverbal IQ (which involves no reading) and reading comprehension scores was .47. The correlation between Verbal IQ and reading comprehension after Nonverbal IQ is partialled out is only .29. The Verbal IQ test obviously measures considerably more than just reading proficiency.

IQ and Learning to Read. Pupils’ major task in the primary grades (i.e., Grades 1 to 3) is learning to read. There are two main aspects of reading skill: decoding and comprehension. Decoding is the translation of the printed symbols into spoken language, and comprehension, of course, is understanding what is read. The learning of decoding (also called oral reading) is somewhat less predictable from IQ than is reading comprehension, which, once decoding skill has been achieved, quite closely parallels mental age. When elementary school children (all of the same age) are matched on decoding skill, their rank on a test of reading comprehension is practically the same as on IQ. In fact, reading comprehension per se is almost indistinguishable from oral comprehension once decoding is acquired. Most students with poor reading comprehension perform no better on tests of purely oral comprehension. But the reverse does not hold: there are some children (and adults) whose oral comprehension is average or superior, yet who have inordinate difficulty in the acquisition of decoding. When such disability is severe and unamenable to the ordinary methods of reading instruction, it is referred to as developmental dyslexia. Dyslexia seems to be a specific cognitive disability that does not involve g to any appreciable extent. Some dyslexics obtain high scores on both the verbal and nonverbal parts of individual IQ tests that require no reading, and they can be successful in college courses, especially in mathematics, physical sciences, and engineering, provided that someone reads their textbooks to them. There is no deficiency in comprehension per se. The vast majority of poor readers, however, are poor readers not because they lack decoding skill, but because they are deficient in comprehension, which, as measured by standard tests of reading comprehension is largely a matter of g (E. L. Thorndike, 1917; R. L. Thorndike, 1973-74.)

Here are some typical results. The Wechsler Preschool and Primary Scale of Intelligence (WPPSI), which does not involve reading, was given to children in kindergarten prior to any instruction in reading and was correlated with tests of reading achievement in first grade after one year’s instruction in reading (Krebs, 1969). Achievement was measured by the Gilmore Oral Reading Test (a test of decoding) and the reading subtests of the Stanford Achievement Test (SAT), which involves word meaning and paragraph comprehension as well as decoding. The one-year predictive validities of the WPPSI IQ scales are as follows:

WPPSI                              Gilmore Oral Reading     SAT Reading Comprehension
Verbal Scale IQ                                 .57                                            .61
Performance Scale IQ                     .58                                            .63
Full Scale IQ                                     .62                                            .68

When the sample was divided into lower- and upper-socioeconomic-status groups, it was found that the predictive validity of IQ was higher in the lower-SES group than in the higher-SES group (e.g., SAT reading scores correlated .66 versus .40 with Full Scale IQ).

Group tests of reading readiness look a good deal like group IQ tests in item content. They are intended to predict reading achievement in the primary grades and can be taken by children prior to having received any instruction in reading. Lohnes and Gray (1972) factor analyzed seven reading readiness tests and an IQ test given to 3,956 pupils in 299 classrooms in the first weeks of the first grade, before they could read. The IQ test correlated .84 with the general factor (i.e., first principal component) common to the reading readiness tests, a higher correlation than that of any of the readiness tests themselves, which showed correlations with the general factor ranging from .44 to .81, with a median of .60. Two years later, when the same pupils were in the second grade, they were given ten reading and language achievement tests and one arithmetic computation test. These were factor analyzed, yielding correlations with the general factor of the achievement battery ranging from .64 (arithmetic computation) to .87 (reading vocabulary), with a median correlation of .80. The general factor of the reading readiness battery (including IQ) correlated .81 with the general factor of the achievement battery. Lohnes and Gray conclude:

There is no question that reading skills of pupils were observed by the criterion measurement instruments [i.e., the achievement tests given in second grade]. What these analyses reveal is that the most important single source of criterion variance, or to put it differently, the best single explanatory principle for observed variance in reading skill, was variance in general intelligence, (p. 475)

IQ Not a Stand-in for Socioeconomic Status. The claim has been made that IQ as a predictor of amount of education attained by adulthood is merely a “stand-in” for socioeconomic status. SES is indexed mainly by the father’s occupational status and the educational level of both parents. If a child’s SES determines his educational achievement or number of years spent in school, we should not expect to find a significant correlation between IQ and years of schooling among brothers reared together in the same family. Yet among brothers there is a correlation of about .30 to .35 between IQ and years of schooling as adults when IQ is measured in elementary school. (This correlation can be inferred from data presented by Jencks, 1972, p. 144.) Within-family differences in educational attainments for same-sex siblings cannot be attributed to differences in SES, “cultural differences,” or “family background.”

A study in Britain (Kemp, 1955) determined the correlations among IQ, tested scholastic achievement, and SES, with all of the intercorrelated variables consisting of the mean values obtained on these characteristics in fifty schools. The intercorrelations were as follows:

IQ and scholastic achievement      = .73
IQ and SES                                        = .52
SES and scholastic achievement   = .56

When IQ is partialled out (i.e., held constant statistically) of the correlation between SES and scholastic achievement, the partial correlation drops to .30. However, when SES is partialled out of the correlation between IQ and achievement, the partial correlation drops only to .62. This means that IQ independently of SES determines achievement much more than does SES independently of IQ.

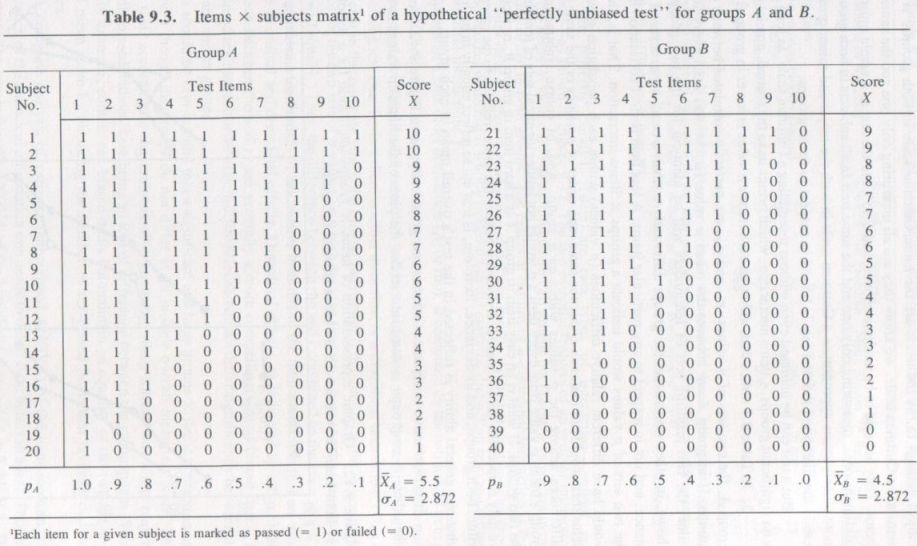
Because father’s education and occupation are the main variables in almost every composite index of SES or “family background,” it is instructive to look at the degree of causal connection between these variables and a child’s early IQ (at age 11), the child’s level of education (i.e., highest grade completed) attained by adulthood, and the child’s IQ as an adult. The intercorrelations among all these variables were subjected to a “path coefficients analysis” by the biometrician C. C. Li (1975, pp. 324-325).

Path analysis is a method for inferring causal relationships from the intercorrelations among the variables when there is prior knowledge of a temporal sequence among the variables. For example, a person’s IQ can hardly be conceived of as a causal factor in determining his or her father’s educational or occupational level. The reverse, however, is a reasonable hypothesis. The path diagram as worked out by Li (from data presented by Jencks, 1972, p. 339) is shown in Figure 8.4.

In path diagrams the observed correlations are conventionally indicated by curved lines (e.g., the observed correlation of .51 between father’s education and father’s occupation). The temporal sequence goes from left to right, and the direct paths, indicating the unique causal influence of one variable on another independently of other variables, are represented by straight lines with single-headed arrows to indicate the direction of causality. (Arrows that appear to lead from nowhere (i.e., from unlabeled variables) represent the square roots of the residual variance that is attributable to variables that are unknown or unmeasured in the given model.) We see in Figure 8.4 that the direct influences of father’s education and occupation contribute only .14² + .20² = 6 percent of the variance in the child’s final educational attainment (i.e., years of schooling) as an adult, whereas the direct effect of the child’s IQ at age 11 in determining final educational level is .44², or 19 percent of the variance. In brief, childhood IQ determines about three times more of the variance in adult educational level than father’s educational and occupational levels combined. Notice also that the father’s education and occupation combined determine only .20² + .20² = 8 percent of the variance in childhood IQ. Li concludes: “The implication seems to be that it is the children with higher IQ who go to school rather than that schooling improves children’s IQ. The indirect effect from early IQ to adult IQ via education is (0.44)(0.25) = 0.11” (p. 327).

Occupational Level, Performance, and Income

It is a consistent finding in all the studies of occupations and IQ that the standard deviation of scores within occupations steadily decreases as one moves from the lowest to the highest occupational levels on the intelligence scale. In other words, a diminishing percentage of the population is intellectually capable of satisfactory performance in occupations the higher the occupations stand on the scale of occupational status. Almost anyone can succeed as a tomato peeler, for example, and so persons of almost every intelligence level except the severely retarded may be found in such a job. But relatively few can succeed as a mathematician; no persons in the lower half of the intelligence distribution are to be found in this occupation in which nearly all who succeed are in the upper quarter of the population distribution of IQ. Thus the lower score of the total range of scores in each occupation is much more closely related to occupational status than is the upper score of the range.

Tested Ability and Performance within Occupations. The IQ and other ability test scores are considerably better at predicting persons’ occupational statuses than at predicting how well they will perform in the particular occupational niche they enter. Some one-fourth to one-half of the total IQ variance of the employed population is already absorbed in the allocation of persons to different occupations, so that there is less IQ variation left over that can enter into the correlation between IQ and criteria of success within occupations.

Restriction of range, however, is not the major factor responsible for the often low correlations between test scores and job performance. For one thing, in the vast majority of jobs, once the necessary skills have been acquired, successful performance does not depend primarily on the ability we have identified as g. Other traits of personality, developed specialized skills, experience, and ability to get along with people become paramount in job success as it is usually judged. It has been said that in the majority of jobs, as far as employers are concerned, the most important ability is not intellectual ability but dependability.

IQ and Creativity

Critical reviews of attempts to measure creativity have concluded that various creativity tests show hardly any higher correlations with one another than with standard tests of intelligence (Thorndike, 1963b; Vernon, 1964). The g factor is common to both kinds of tests, and there seems to be no independent substantial general factor that can be called creativity. Besides g, creativity tests involve long-recognized smaller group factors usually labeled as verbal and ideational fluency. Differences between persons scoring high and persons scoring low on “creativity” tests, when they are matched on IQ, invariably consist of descriptions of personality differences rather than of characteristics that would be thought of as any kind of ability differences. Thus “creativity,” at least as presently measured, apparently is not another type of ability that contends with g for importance, as some writers might lead us to believe (Getzels & Jackson, 1962; Wallach & Kogan, 1965). While “creativity” tests may be related to certain personality characteristics, they have not been shown to be related to real-life originality or productivity in science, invention, or the arts, which are what most people regard as the criteria of creativity.

For a time it was believed that the research of Wallach and Kogan (1965) contradicted the conclusion of earlier reviews to the effect that “creativity” and intelligence are not different co-equal abilities or even factorially distinguishable traits. Wallach and Kogan had claimed that the failure of earlier researches to separate creativity and intelligence was a result of the fact that the creativity tests were usually given in the same manner as the usual psychometric tests, with time limits, as measures of some kind of ability, in an atmosphere conducive to competitiveness and self-critical standards. These conditions, it was maintained, were antithetical to the expression of creativity. So Wallach and Kogan gave their tests of creativity (better labeled as fluency) without time limits, in a very free, nonjudgmental, play-like, game-like atmosphere. Under these conditions, they found negligible correlations between several verbal intelligence tests and their “creativity” tests. The “creativity” scores, however, account for only a small percentage (2 percent to 9 percent) of the variance in any of the dependent variables measured in this study. High scorers in general tended to be less inhibited or less constricted in producing responses; they responded more energetically and fluently in the game-like setting in which the “creativity” tests were given. [...]

If there were actually no relationship of any kind between creativity and intelligence, as some popular writers would have us believe, we should expect to find the same proportion of mentally retarded persons (with IQs below 70) among the acknowledged creative geniuses of history as is found in the general population. Biographical research on the childhoods of famous creative persons in history, however, has revealed that in 300 cases on whom sufficient data were available, all of them without exception showed childhood accomplishments that would characterize them as of above-average intelligence, and the majority of them were judged to be in the “gifted” range above IQ 140 (Cox, 1926).

Donald W. MacKinnon has actually obtained the Wechsler (WAIS) Full Scale IQs of 185 noted architects, mathematicians, scientists, and engineers who were selected from a national sample on the basis of ratings by other professionals in these fields as being among the most creative contributors to these socially significant fields (MacKinnon & Hall, 1972). In this highly select group, the judged ranking in creativity correlated only +.11 with WAIS IQ. But the more important fact, which is often neglected in popular accounts, shows the threshold relationship of IQ to creativity: the total IQ variance in this group of creative persons is less than one-fourth of the IQ variance in the general population. The entire creative sample ranges between the 70th and 99.9th percentiles of the population norms in IQ (i.e., IQs from 107 to 151), with the group’s mean at the 98th percentile (IQ 131). To the extent that these groups are typical of persons whom society regards as creative, it can be said that some 75 to 80 percent of the general population would be excluded from the creative category on the basis of IQ alone. [...]

Chapter 9 Definitions and Criteria of Test Bias

The Criterion Problem. ... A biased criterion is one that consistently overrates (or underrates) the criterial performance of the members of a particular subpopulation. A good example is sex bias in school grades: teachers generally give slightly higher grades to girls than to boys, even when the sexes are perfectly matched on objective measures of scholastic achievement.

When the criterion itself is questionable, we must look at the various construct validity criteria of test bias. If these show no significant amount of test bias, it is likely (although not formally proved) that the criterion, not the test, is biased. In a validity study, poor criterion measurement can make a good test look bad.

Correlation between Test and Construct

Construct validity may be defined theoretically as the correlation between test scores X and the construct C the test is intended to measure, that is, rXC. In reality, of course, the problem is that we have no direct measure of C. And so the process of construct validation is roundabout, consisting mainly of showing in more and more different ways that the test scores behave as should be expected if, in fact, the test measures the construct in question. Thus construct validity rests on a growing network of theoretically expected and empirically substantiated correlations and outcomes of specially designed experiments to test the construct validity of the measuring instrument.

Rarely would it be claimed that any single test is a perfect measure of a complex theoretical construct such as intelligence. A test score is viewed as merely an imperfect index of the construct itself, which is to say that, for any given test that attempts to measure the construct, the correlation rXC is less than 1, even after correction for attenuation (unreliability). If, for example, we define the construct of intelligence as the g factor common to an indefinitely large and diverse battery of mental tests, the construct validity (or, more narrowly, the factorial validity) of a given IQ test is estimated by its g loading when it is factor analyzed among a large battery of other tests. The variance contributed by any given test’s group factors, specificity, and unreliability, of course, all tend to lower the test’s correlation with g.

Because no single test is a perfect measure of the construct that it aims to measure, what is the consequence of this one fact alone for group mean differences on such an imperfect test?

Considerable conceptual confusion on this theoretically important point has been introduced into the literature on test bias by Block and Dworkin (1974, pp. 388-394). These writers state:

Given linearity [of the regression of IQ scores on the hypothetical construct of intelligence] and the obvious fact that IQ tests are less than perfect as measures of intelligence, a rather surprising conclusion follows: if IQ tests are color-blind on an individual basis, they are likely to be biased against racial groups, such as blacks, which score below the population mean. (p. 388)

There follow three pages of statistically fallacious reasoning by Block and Dworkin to prove that, even if the test is unbiased for individuals, the observed black-white mean IQ difference of 15 points (85 versus 100) is greater than the true intelligence difference, since IQ is only an imperfect measure of intelligence. They say, “Thus, on the average, people with below-average IQs have their intelligence underestimated by IQ tests.... It follows that the black intelligence expected on the basis of IQ is higher than 85” (p. 389).

In fact, Block and Dworkin’s argument is entirely wrong, and just the opposite conclusion is correct. The fallacy in their reasoning is due to their failure to recognize that (1) a group mean (and consequently a group mean difference) is a statistically unbiased estimate of the population value, (2) the reliability or validity of the measurements do not in themselves systematically affect the sample mean, and (3) removal of the error variance and the variance that is nonrelevant to the construct (assuming that the groups do not differ on the nonrelevant factors, which is presumably what Block and Dworkin mean by the test’s being “color-blind on an individual basis”) would actually create a larger difference between the black and white group means when measured in standard deviation units or in terms of the percentage of overlap of the two distributions.

To put it in more general terms, assume that on a particular test two populations A and B differ in observed means, X‾A-X‾B; and assume that the test’s construct validity is rXC in both groups and that the test is color-blind on an individual basis; that is, it measures no factors on which the groups differ other than the construct purportedly measured by the test. Then the group mean difference on the construct itself, expressed in standard deviation (σ) units will be D‾A-B = (X‾A-X‾B)/σrXC. Thus, when the test is an imperfect measure of the construct, that is rXC < 1, the mean score difference between two groups underestimates the group mean difference in the construct itself, by an amount proportional to rXC. If we wish to retain the same measuring scale and the same σ for the construct as for the obtained scores, the group mean difference on the construct will be simply D‾A-B = (X‾A-X‾B)/rXC. Thus, for example, Block and Dworkin (p. 389) assume the construct validity of IQ to be 0.50, in which case the observed white-black mean IQ difference of 15 points would represent a true intelligence difference, measured on the same scale, of D‾ = (100 - 85)/0.50 = 30 points. (Probably for the purposes of their argument, Block and Dworkin assumed an excessively low value of .50 for the construct validity of IQ. Values in the range from .70 to .90 are probably closer to the truth, which would make the true mean intelligence difference between blacks and whites equivalent to only some 17 to 21 points on an IQ scale, or about 1.1σ to 1.4σ.)

Because a test underestimates group mean differences in a latent trait to the extent that the test’s construct validity falls short of perfection, it would not be surprising, consequently, to find that improvement of a test’s construct validity can actually augment group mean differences, if the groups in fact differ in the latent trait that the test attempts to measure and do not differ in other factors that the test might measure. A test fails to be color blind and may be regarded as biased to the extent that it measures group differences that are irrelevant to (i.e., uncorrelated with) the test’s construct validity.

What we need to be sure of, of course, is that the test measures the same construct equally well in the various populations in which it is intended for use and does not also measure some other characteristic on which the groups differ but which is uncorrelated with the construct purportedly measured by the test. The probability that these conditions are true is increased by showing that the groups do not differ in certain other properties of the test besides its construct validity. Every validity coefficient the test demonstrates in terms of various external criteria, when the validity coefficient is the same in the major and minor groups, is an additional point of evidence increasing the probability that the test is an unbiased measure of the same construct in both groups.

Groups x Items Interaction. The statistical concept of interaction, derived from the analysis of variance, provides the basis for several of the most important objective techniques available for detecting test bias. [...]

Probably the easiest way to grasp the concept of a groups X items interaction is to examine the complete data matrix of a hypothetic test for which the groups X items interaction is zero, despite the fact the groups differ in their overall means. Such a test can be regarded as unbiased in the statistical sense of a failure to reject the null hypothesis. More accurately, we would say that a potential indicator of bias, namely, a groups X items interaction significantly greater than zero, has failed to materialize, and therefore we cannot reject the null hypothesis, which states that there is no groups X items interaction. With failure to reject the null hypothesis, all we can conclude is that there is no evidence of bias, which, of course, does not prove that bias does not exist. But in statistics it is axiomatic that the null hypothesis can never be proved. If, however, a significant groups X items interaction were found, we could then reject the null hypothesis and conclude that the test items are subject to some kind of bias, possibly cultural, with respect to the two groups under consideration. [...]

The complete data matrix (more specifically termed “items x subjects matrix”) of a hypothetic perfectly unbiased test is shown in Table 9.3. For the sake of simplicity, this “test” has only ten items, and we have administered it to only twenty “subjects” in each group. Groups A and B are assumed to be random samples drawn from populations A and B. (In practice, A and B may be different ethnic groups, social classes, nationalities, religions, sexes, etc.) Also, to simplify inspection of the matrix, the subjects in each group are arranged in the order going from the highest to the lowest test scores (see column headed Score), and we have arranged the test items in the order of their p values (proportion passing), from the easiest to the hardest (see rows labeled pA and pB). Two conspicuous features of Table 9.3 should be noted.

1. In both groups the test items are a perfect Guttman scale. This means that, if we know any subject’s total score on the test, we also know exactly which items he or she passed or failed; and, of course, we also know that any two subjects with the same score have passed or failed exactly the same items. This is true irrespective of which group a subject belongs to, as the items are the same Guttman scale in both groups. When the items are a Guttman scale, we know they are all measuring only one and the same trait or factor. They are said to be unidimensional, and ipso facto the test as a whole must also be unidimensional, measuring only one and the same trait in all subjects in both groups. The more closely items approximate a Guttman scale in both the major and minor groups, the less is the likelihood that the test is biased in respect to these groups.

But a test can be unbiased even without resembling a Guttman scale, as long as there is no significant groups X items interaction, which brings us to the second, crucial point.

2. In Table 9.3 notice that, although each item’s p value is lower in group B than in group A, the two sets of p values, pA and pB, are perfectly correlated between the two groups. If in group A we subtract the mean p value (p‾A = .55) from every item’s p value, the two resulting sets of remainders will be identical for the two groups. This shows, in other words, that the groups differ only in their overall mean level of performance, and not in respect to any particular items. A less than perfect correlation between the two sets of p values would indicate a groups X items interaction. That is, the items would have different relative difficulties (p values) within each population group. The items then would not maintain either the same rank order of p values or the same relative differences among the p values within each group. And, of course, subtracting each group’s mean p value from every item’s p would not render identical sets of remainders in the two groups. If what is an easy item in group A is a hard item in group B, or vice versa, we may suspect the item is biased. It does not behave the same, relative to the other items, within both groups; and its deviance, therefore, is less apt to reflect equally in both groups whatever general ability is reflected in the test’s overall mean in each group.

It is instructive to represent interactions graphically, as in Figure 9.12. Note that, when there is no groups X items interaction, the plots of the items’ p values in the two groups are perfectly parallel. There are two types of interaction - ordinal and disordinal - as shown in Figure 9.12. The two essential features of an ordinal interaction are (1) the items’ p values are not parallel in the two groups but (2) the p values are in the same rank order in both groups. The essential feature of a disordinal interaction is that the p values have a different rank order in the two groups. (Whether the two lines cross over one another or do not is wholly irrelevant to the essential distinction between ordinal and disordinal interactions.)

Spearman’s rank order correlation (p, or rho), if computed on the two sets of item p values, will be 1 when there is no interaction and also when there is ordinal interaction. The Pearson r computed on the same data will be 1 when there is no interaction and will be something less than 1 when there is either an ordinal or a disordinal interaction. (This is true except in the rare case where the ordinal interaction is due only to a difference in the variances of the two sets of p values, in which case the Pearson r between the two sets of p values will equal 1.) Thus, the difference between rho and r computed on the same sets of p values provides an indication of the relative amounts of the total interaction that are attributable to ordinal and disordinal effects. Disordinal effects, as indicated by a significant difference between rho and r, are generally a more compelling sign of biased items. In an unbiased test the rank order of item difficulties should not differ significantly between the major and minor groups.

It should be kept in mind that a significant and large groups x items interaction can exist even though the groups do not differ at all in their overall mean test score. This means that, according to the criterion of a groups x items interaction, a test may be markedly biased without there being an iota of difference between the group means. Some tests, for example, contain sex-biased items but maintain an equality of the two sexes in overall mean score by balancing the number of sex-biased items that favor or disfavor each sex.

A complete analysis of variance (abbreviated ANOVA) of the item score matrix yields much of the statistical information one needs to detect item biases in a test. This can be illustrated by presenting the ANOVA of the hypothetic data matrix in Table 9.3. The results of the ANOVA are given in Table 9.4. This kind of table will look familiar to readers who are versed in the analysis of variance. (The computations involved in the ANOVA cannot be explicated here; they can be found in most modem statistics textbooks and are a standard part of advanced courses in statistical methods.) The first four columns of figures in Table 9.4 are the usual ANOVA, which tabulates the sample values of the mean square (MS) by dividing the sum of squares (SS) by its degrees of freedom (df). The variance ratio F is the ratio of two mean squares and tests the statistical significance of a given source of variance. An F value less than 1 is always interpreted as nonsignificant in this context. An F greater than 1 is significant or not depending on the df associated with the numerator and denominator that entered into the F ratio. In our example, the between-groups F = 1.15, with 1 and 38 df, is nonsignificant; that is, we cannot reject the null hypothesis, namely, that the populations of which the groups A and B are random samples do not differ in means on this particular test. The differences between item means (i.e., item p values) with F = 38 (1 and 342 df) are highly significant, as are the differences between the individual subjects within each group.

The groups x items interaction MS is zero, which means the items maintain exactly the same relative difficulties within each group. If the groups x items interaction term were greater than zero, it would be tested for significance by the F ratio = the groups x items MS/subject x items MS, with 9 and 342 df.

The last column in Table 9.4 gives eta squared. Eta squared merely indicates the proportion of the total variation in all the data contributed by each source. It is an important calculation for our purposes, because we wish to know not only the statistical significance of any given source of variance, but also its size relative to other sources of variance. A source of variance that may be significant in the statistical sense may also be so small a percentage of the variance as to be utterly trivial for any practical considerations.

Rank Order of Item Difficulties and Delta Decrements. The groups x items interaction is composed of ordinal and disordinal components and their interaction. The disordinal component is the result of items having a different rank order of difficulties (i.e., p or Δ values) in the major and minor groups. The ordinal component is a result of relative differences in item difficulties that nevertheless have the same rank order of difficulty in both groups. The interaction of the ordinal and disordinal components reflects differences in the relative difficulties of items owing to their having different rank orders of difficulty in the two groups.

If the groups x items interaction in the ANOVA of the items x subjects x groups matrix is significant, we may wish to analyze the interaction further to determine whether it is due mostly to ordinal or disordinal group differences in item difficulties. Or, even if the groups x items interaction is not significant, we may wish further to demonstrate the degree of similarity between the groups by showing the degree of their similarity on the ordinal and disordinal effects separately.

This analysis can be achieved by the following method:

1. All the test items are simply ranked for difficulty within groups A and B, and Spearman’s rank order correlation, rho or pAB, is computed between the two sets of ranks. (It makes no difference whether we rank the item p values or Δ values, as they have exactly the same rank order.) The coefficient p is a correlation coefficient, interpreted like the Pearson r. In this case p indicates the degree of similarity between the groups in the order of item difficulties. The value of 1 - p² estimates the proportion of the groups X items interaction variance attributable to the purely disordinal aspect of the groups x items interaction.

2. Within the major group, the n items of the test are ranked in the order of their Δ values, going from the largest to the smallest. The items are arranged in exactly the same order in the minor group (regardless of the items’ actual order of difficulty in the minor group).

3. Then the Δ decrements are obtained within each group. A Δ decrement is the difference in Δ values between adjacent items when the items are ranked as just described. [14] For example, if there are four items, numbered 1 to 4, which in the major group have a rank order of A values of 1, 2, 3, 4, respectively, then the A decrements will be Δ1 - Δ2, Δ2 - Δ3, and Δ3 - Δ4. In the major group all the Δ decrements are necessarily zero or greater than zero. It can be seen that all the inter-item variance (in the major group) due to the rank order of item difficulties is completely eliminated by this procedure, leaving only the variance due to the unequal difficulty decrements between items.

4. Finally, we compute the Pearson r between the Δ decrements of the major and minor groups. The r indicates the degree of group resemblance in relative item difficulties when the rank order of item difficulties is eliminated, and r² is the proportion of variance in the minor group’s Δ decrements that is predictable from the items’ Δ decrements in the major group. The value p²(1 - r²) is the proportion of the groups x items interaction variance that is due to group differences in the relative difficulties of items over and above that which is attributable to the items’ differences in rank order; in other words, it is the purely ordinal component of the groups x items interaction. The residual proportion of the groups x items interaction variance, that is, the part attributable jointly to the interaction of group differences in the ordinal and disordinal aspects of item difficulties, is p²r². The following table summarizes the analysis of the groups x items interaction variance, where p is the rank order correlation between the groups’ item difficulties and r is the Pearson correlation between the groups’ Δ decrements:

Source of Interaction Variance                                                 Proportion of variance

Disordinal, i.e., group differences in rank order of item difficulties     1-p²
Ordinal, i.e., group differences in Δ decrements                                   p²(1-r²)
Residual, i.e., interaction of disordinal x ordinal                                      p²r²

The Item Characteristic Curve. ... The ICC is a graph of the percentage passing an item as a function of total raw score on the test. [15]

If the test scores measure a single ability throughout their full range, and if every item in the test measures this same ability, then we should expect that the probability of passing any single item in the test will be a simple increasing monotonic function of ability, as indicated by the total raw score on the test. Ideally, the function approximates the ogive of the normal curve. Persons with more of the ability (i.e., a higher score) measured by the test should, on the average, have a higher probability of passing any given item in the test than persons with less ability (i.e., a lower score). The graph of this relationship of the percentage of all persons at each raw score who pass a given item is the item characteristic curve (ICC). The ICCs of three items are shown in Figure 9.13.

Item 1 is an example of a defective item, as revealed by the anomalous ICC. An item with such an ICC should be eliminated from the test, as the percentage passing the item is not a monotonically increasing function of the raw score. Persons of high ability on the test as a whole do less well on item 1 than do persons of intermediate ability. In many cases, the nature of the item’s defect can be inferred from a critical examination of the item. For example, the following item from a college test of general cultural knowledge produced an ICC like that of item 1 in Figure 9.13. [...]

Items 2 and 3 both show highly acceptable ICCs. Item 3 is obviously much more difficult than item 2.

Notice that the ICC does not depend on the form of the distribution of raw scores. Therefore, if the test measures the same ability in two or more different groups, we should expect the groups to have the same ICC for any given item in the test, regardless of any difference between the groups in the distribution of total scores on the test.

Hence, a reasonable statistical criterion for detecting a biased item is to test the null hypothesis of no difference between the ICCs of the major and minor groups. In test construction, the items that show a significant group difference in ICCs should be eliminated and new ICCs plotted for all the remaining items, based on the total raw scores after the biased items have been eliminated. The procedure can be reiterated until all the biased items have been eliminated. The essential rationale of this ICC criterion of item bias is that any persons showing the same ability as measured by the whole test should have the same probability of passing any given item that measures that ability, regardless of the person’s race, social class, sex, or any other background characteristics. In other words, the same proportions of persons from each group should pass any given item of the test, provided that the persons all earned the same total score on the test. In comparing the ICCs of groups that differ in overall mean score on the test, it is more accurate to plot the proportion of each group passing the item as a function of estimated true scores within each group (rather than raw scores on the test), to minimize group differences in the ICCs due solely to errors of measurement.

Chi squared provides an appropriate statistical test of the null hypothesis in this case. For a given item, one determines the obtained frequencies O and the expected frequencies E of passes (+) and failures (-) in the major (A) and minor (B) groups for each total score. The obtained frequencies 0+A and 0+B and 0-A and 0-B are simply the numbers of persons with a given total score in the major or minor groups who passed or failed the given item. Under the hypothesis that the groups do not differ, the expected frequency for group A is EA = NA(0A + 0B)/(NA + NB), and for group B it is EB = NB(0A + OB)/(NA + NB), where NA and NB are the total number of persons in groups A and B, respectively, who earned the same total score on the test. Chi squared, then, is

(∑ indicates that the expression within the brackets is summed over all of the total score cohorts.) The χ² has s(g-1) degrees of freedom, where g is the number of groups and s is the number of total score cohorts. (This method can of course be adapted for any number of groups.)

A disadvantage of this method is that it requires a very large sample size in both the major and minor groups, as χ² should not be computed in any cohort in which the expected frequency, either EA or EB, is less than 10. The usual way of handling the computation of χ² when any E is less than 10 is to combine enough adjacent score cohorts to yield E’s of 10 or more. If the samples are not especially large, it may be necessary to combine as many as five or six adjacent score cohorts to yield sufficiently large E’s from which to calculate χ². The statistical precision of the method is slightly weakened, of course, if the major and minor groups’ scores are not proportionally distributed the same within each combined score interval, and usually they will not be distributed the same if there is a marked difference between the overall groups’ means. The overall lower group will tend to have the lower mean score within any score interval. This can be corrected by eliminating persons from the larger group to make the proportional distributions of scores within the interval nearly the same for both groups. When this is done, even quite coarse grouping, creating as few as five or six score intervals in all, can result in a satisfactory chi squared test of item bias.

Usually not all significantly biased items are biased in the same direction. Some item biases favor the major group and some favor the minor group in the total score. One can estimate the net amount of directional bias by determining the difference between the group means when the significantly biased items are included in the total score on the test and when they are excluded. A t test for correlated means can then be applied to determine whether this mean difference is statistically significant (see Guilford, 1956, p. 186). The outcome of such an analysis would indicate whether the various item biases in the test significantly favor the major or the minor group in the overall score. However, the test may be biased whether or not it systematically favors one group, if there is a larger number of significantly biased items than could be expected by chance alone. A test composed of a large proportion of significantly biased items, some that favor the major and some the minor group, but in which the item biases are balanced out so as not to favor either group in the overall test score, cannot be claimed to measure one and the same ability on the same scale in both groups.

Item Correlation Methods. In test construction, one of the principal criteria for item selection is the item’s correlation with total score on the test. Items that do not correlate significantly with the total score cannot contribute to the true variance in test scores but only to the error variance; they are therefore discarded in the process of test construction. Items, of course, differ in their degree of correlation with the ability measured by the test, as indexed by the total score, so that there is always a range of item x total score correlations, all of which are distributed significantly above zero in a well-constructed test.

In an unbiased test ideally the item X score correlation for any given item should be the same in the major and minor groups. Unfortunately, this hypothesis is difficult to test rigorously, for three reasons: (1) the item X score correlation has a rather large sampling error, (2) the item X score correlations are usually fairly homogeneous, and (3) the item X score correlation is affected by the difficulty of the item, so that if the difficulty of the item is markedly different in the major and minor groups, the item X score correlations in the two groups will not be directly comparable. (The biserial correlation [16] rb seems preferable to the point-biserial correlation rpbi because it is somewhat less affected by item difficulty.) Despite these limitations, certain indications of bias may be gleaned by comparing the item X score biserial correlations in the major and minor groups. The frequency distributions of all the rb values for the n items in the test should be approximately the same for both groups. The number of nonsignificant correlations should be very few and not differ significantly in the two groups. When nonsignificant correlations are found, one should look for ceiling or floor effects, that is, extremely easy or extremely difficult items, that result in low correlations because of the restriction of variance on the item. We should also expect to find a significant positive correlation between the item X score biserial correlations of the major and minor groups, although this correlation could be greatly attenuated by the homogeneity of rb, sampling error, and perturbations due to group differences in item difficulty. No one has yet devised a satisfactory statistical test of the overall significance of the differences between the major and minor group’s item X score biserial correlations. However, the most probably biased items may be identified as those for which the item X score biserial correlation differs between groups by more than twice the standard error of the difference between the rb values.

The item X test biserial rb makes possible the testing of a hypothesis of considerable interest. If the test measures the same ability in the major and minor groups, and if the groups differ on this ability measured by the score on the whole test, then we should expect that the items that best measure ability within each group (i.e., those items with the largest item X score rb) should also discriminate most between the groups. This hypothesis can be tested by first obtaining the item X score rb for every item, within each group, then obtraining the item x groups correlation (phi/phi max), [17] and finally obtaining the correlation (r) between rb and phi/phi max over all of the items, for each group. If this correlation is positive and significant, the hypothesis is borne out; namely, those items that correlate most highly with the ability measured by the test within each group also discriminate most highly between the groups. By splitting the major group (and the minor group) into random halves and performing this analysis in the two halves, one can determine if the correlation between the item X score correlation and item X groups correlation is significantly larger for the split-halves of the same group or for the split-halves across the major and minor groups. A same-group split-halves correlation significantly larger than the across-groups split-halves correlation would indicate bias.

Factor Analysis Criteria of Bias. In the first part of this chapter it was noted that a test can be regarded as unbiased if it predicts the performance of different persons on an external criterion with equal accuracy regardless of their group memberships. One condition that we should expect if this is true is that the correlation between test scores and criterion measures should be the same in the major and minor groups.

The test and the criterion are correlated because they share certain factors in common. If, for example, the test score X measures a single factor F in common with the criterion measures C, then the correlation rXC between test scores and criterion measures can be expressed as the product of their correlations with the common factor, that is, rXC = rXF x rCF. Therefore, if the test score measures different factors in the major and minor groups, that is, if rXF is different in the two groups, then it is highly improbable that rXC will be the same in both groups. (It could conceivably be the same, however, if the test measured two different factors, F1 and F2 in the major and minor groups, respectively, and yet each factor had exactly the same correlation with the criterion, that is, rF1C = rF2C.) If it can be shown that rXF is significantly different in the major and minor groups, it is so highly likely that the test will predict a criterion differentially for persons depending on their group membership as to constitute strong evidence of bias. As Humphreys and Taber first pointed out,

Regression differences can confidently be expected across groups . . . if the initial factor analyses of scores in the two groups indicate factorial dissimilarity. Comparability of factors and factor loadings in the groups is not a necessary condition for near identity of slopes of regression lines in the mathematical sense, but the probability that factor loadings of a given criterion would exactly compensate for differences in predictor loadings is very small. If the predictors are to be used for several criteria, the probability that factor loadings for every criterion will compensate for differences in predictors becomes vanishingly small. . . . If factor loadings are comparable, it is reasonable to expect parallel or very nearly parallel regression lines for advantaged and disadvantaged groups. (Humphreys & Taber, 1973, pp. 107-108)

Thus, factor analysis of a test or a battery of tests or other predictors in adequate samples of the major and minor groups can be used to detect predictive bias indirectly, without need for the more time-consuming and expensive direct determination of the test’s predictive validity in terms of an external criterion.

The concept of construct validity also implies that the test score variance has the same factorial composition in the major and minor groups.

Therefore, if we can reject the null hypothesis that there is no difference between groups in the factorial composition of their test scores, we can claim that the test is biased. For this statistical purpose, a principal components analysis seems preferable to any rotated factor solution, because the process of factor rotation itself can magnify the effects of sampling errors in the basic correlations. (However, rotated factors may be more amenable to psychological interpretation). Furthermore, if we are concerned about bias in the total score on the test (or test battery), our attention should be primarily focused on the first principal component, as it accounts for the largest proportion of the variance in total scores. The variance of total scores on a good test is concentrated mostly in the first principal component, and, therefore, we should be most concerned that the first principal component is the same, within the margin of sampling error, in the major and minor groups if the test scores are to be interpreted as unbiased measures.

Principal components analysis can be applied to the matrix of correlations among the single items comprising the test or to the correlations among subtests (homogeneous groups of items) that make up the total test. If items are used, the item intercorrelations should be obtained by phi/phi max, so that group differences in item difficulty will not enter into the matrix of intercorrelations and produce a “difficulty factor” on which the major and minor groups may differ. As emphasized previously, a group difference in difficulty cannot itself be a criterion of test bias, because it completely begs the question of whether the groups differ because of test bias or because of some other factors.

Since either items or subtests may be subjected to principal components analysis, for simplicity we shall henceforth refer to either item scores or subtest scores as units of the test. A principal components analysis of the units is performed in the major and minor groups separately. Two questions, then, must be answered: (1) “Do the same factors emerge in the major and minor groups?” and (2) “Do the units have the same factor loadings in the two groups?” Both conditions are important, because, even if the test measures the same factors in both groups but the units have different loadings on the factors in the two groups, the factors will be weighted differently in the total score depending on the person’s group membership. The total score, therefore, would not be an equivalent measure for persons from different groups, even when such persons have numerically equal scores. An objective criterion, such as varimax, for orthogonal rotation of the principal components to approximate simple structure facilities identification of the factors measured by the test. The same criterion for the number of principal components to be rotated, such as retaining only those components with eigenvalues greater than 1, should apply to both the major and minor groups. Simple inspection of the rotated factors usually reveals whether the same factors have emerged in both groups, although sophisticated statistical tests of factorial invariance across groups have been devised (e.g., McGaw & Joreskog, 1971).

If one of the two groups yields one or more different or additional factors than are found in the other group, it is instructive to examine the units that contribute the most variance to these factors, that is, the units with the largest factor loadings. They are very likely biased units; discarding them should produce greater factorial similarity of the groups.

Factor analysts have devised rather complex methods for comparing factors across different populations (see Cattell, 1978, pp. 251-270; Kaiser, Hunka, & Bianchini, 1971), but a rough and ready index of factorial similarity that is probably satisfactory for our purpose is simply the Pearsonian correlation between the factor loadings of the major and minor groups for any given factor. This does not provide a statistical test of significance, but only an index of factorial similarity between groups. If the total score of the test is the point of contention with respect to bias, then the correlation between the two groups’ loadings of the test’s units on the first principal component is of primary interest, since the first principal component is the largest source of variance in the total scores. If we can reject the null hypothesis that the groups do not differ on the first principal component, we need go no further and can conclude that the test’s total scores are biased. Elimination of the offending units (i.e., those units whose factor loadings show the greatest discrepancies between groups) may be found to improve the test upon reanalysis, using the same method.

Matched Groups and Pseudogroups. All the foregoing methods of internal analysis for detecting culture bias in tests depend on two basic assumptions. The first basic assumption underlying the foregoing methods of internal analysis is that cultural differences between groups will interact with item content or item types and that group differences in cultural background should not produce equal effects on all of the items in a heterogeneous test. Rejection of this assumption can be cogent only if evidence can be adduced for the presence of some cultural factor that is hypothesized to have a uniformly enhancing or depressing effect across all the items in the test. Such a hypothesis must, of course, be formulated so as to be empirically testable if it is to be of any scientific value.

The second basic assumption underlying the foregoing methods of internal analysis is that cultural groups x items interaction is not perfectly correlated with ability levels x items interaction within the cultural groups. If the test score distributions of the major and minor groups differ in mean or variance and there is a significant groups x items interaction (or other internal indicator of bias), it must be determined whether the interaction is attributable solely to differences in ability level rather than to some other aspect of the group difference. It is quite ossible that ability level interacts with item difficulty, in which case a significant groups x items interaction might reflect only the fact of the groups’ mean difference in the ability measured by the test rather than a difference involving cultural bias. In other words, we need to distinguish between a culture x item interaction and an ability x item interaction. This distinction can be made by means of matched-groups and pseudogroups designs.

In the matched-groups design we test the hypothesis that the major and minor groups, when matched on total test score distributions, do not differ on any of the internal indices of cultural bias, such as groups x items interaction, rank order of item difficulties, correlation of delta decrements, and factorial structure. The hypothesis states, in other words, that there are no features of the test that discriminate between individuals from the major and minor groups who obtain the same total score on the test.

If any of the previously described methods of detecting bias should produce significant results on random samples of the major and minor groups, the method should be reapplied to the major and minor groups after they have been matched on ability, to see if the significant effect was the result of an ability difference between the groups rather than a cultural difference. The best method for obtaining matched groups is to pair up individuals from the major and minor groups with identical total test scores, obtaining as many identically matched pairs of major-minor persons as possible from the available test data. A cultural difference, if it exists, should be detectable by the internal analyses even when the major and minor groups are matched on overall test score. If the result of the analysis is nonsignificant after matching, it can be concluded that the significance of the result from the unmatched groups was due to the groups’ difference in ability level rather than to cultural bias.

The pseudogroups design permits a further test of this hypothesis. In the pseudogroups design a subgroup of persons from the major group is formed that conforms to the distribution of total test scores in the minor group, or vice versa. Thus, we create a pseudo minor group or a pseudo major group for comparison with the real major group or the real minor group, respectively. Then, for example, if the pseudogroups x items interaction is of about the same magnitude as the real groups x items interaction, it is reasonable to conclude that the interaction is due to an ability difference rather than to a culture difference, as the real group and pseudogroup in this analysis are both made up of persons from the same cultural group.

If it is argued that the different ability levels of racial groups are related to social-class cultural differences rather than to racial differences, then one must divide the major and minor groups into subgroups on the basis of social class and test for social class x item interactions, within racial groups. It must also be determined if the social class x items interaction is not attributable to an ability levels x items interaction, by using the matched-group design (i.e., matching social-class groups on overall score and testing the matched groups x items interaction).

The most powerful pseudogroups design for detecting ability x item interaction free of culture x item interaction can be achieved by making up two pseudogroups out of pairs of siblings who differ as much in total test score as do the major and minor groups. Siblings reared together show ability differences, but such differences cannot be due to differences in cultural background. If two groups of siblings, with one member of each sibling pair assigned to each group, are selected so as to reproduce the means and variances of the major and minor groups, and if these two sibling groups then simulate the actual major versus minor groups x items interaction (or other internal indices of bias), it can be presumed that the interaction, and so on, is an ability x items interaction rather than a sign of cultural bias. The only possible alternative conclusion would be that the cultural differences between groups simulate ability differences within either cultural group. This would not seem to be a very compelling conclusion in the absence of independently supporting evidence.

In testing children, age differences in total test score within a given group may be used like pseudogroups formed on the basis of total score. If the internal analyses show major versus minor groups x items interaction, and so on, these may be due to group differences in developmental rates rather than to cultural differences. To test this hypothesis, we repeat the internal analyses, contrasting the major and minor groups each at different ages, to see what happens to the groups x items interaction. The groups x items interaction could disappear when the major group is compared with a minor group one or two years older (or younger). Conversely, one may be able to simulate the major versus minor groups x items interaction by contrasting different age groups within either the major or minor group. The finding that the groups x items interaction can be made to appear or disappear by the manipulation of age of the contrasted samples, between the major and minor groups and within either group, is consistent with the hypothesis that the groups x items interaction is attributable to the major and minor groups’ differential developmental status rather than to cultural bias. The only possible counterhypothesis would be that cultural differences between groups simulate developmental differences within groups in respect to interactions with items, factorial structure of the item intercorrelations, and so on. As an ad hoc hypothesis, this carries no conviction. Independently supporting evidence would be required to lend scientific credibility to this counterhypothesis.

NOTES

[14] Delta decrements should be used rather than p value decrements, as Δ values come closer to representing item difficulties on an interval scale than do p values, as explained earlier in chapter 9. It is a necessary rule that the items must be ranked in the order of the Δ values in the major group for obtaining the Δ decrements. This minimizes the correlation between the Δ decrements of the major and minor groups. Otherwise, various correlations could be obtained depending on the arbitrary order of the items in the test. For example, if the two groups have a similar rank order of item difficulties, it would be possible to produce a spuriously high correlation between the groups’ Δ decrements by ordering the items so as to alternate easy and difficult items. The Δ decrements would then have altematingly positive and negative values in both the major and minor groups, consequently producing a high correlation between the groups. The correlation would represent a complete confounding of ordinal and disordinal effects and hence would defeat the purpose of the analysis here proposed.

Chapter 10 Bias in Predictive Validity: Empirical Evidence

General Caveats in Evaluating Evidence of Bias

Comparison of Validity Coefficients in Major and Minor Groups. If a test’s validity coefficient is the same (i.e., not significantly different) in the major and minor groups, it does not necessarily guarantee that the test is not biased for one group, as the regressions could differ between the groups. But equal validities does mean that the test can be used fairly in both groups, either by using separate regression lines for predicting the criterion in each of the groups or by including group membership as a dichotomous variable in a multiple regression equation. Validity coefficients, therefore, are useful, though limited, for assessing test bias.

The only proper test for possible bias in terms of differential validity is the z test of the significance of the difference between the validity coefficients in the major and minor groups. Some investigators, however, have based a verdict of test bias on the incorrect procedure of testing the validity coefficients, separately within each group, for differing significantly from zero and if the validity differs significantly from zero in one group but not in the other, the test is considered biased. The fault in this method is that the key question as concerns bias is whether the validities are significantly different in the two groups, and this question is not answered by a test of the hypothesis that the validity in one or the other group is not significantly different from zero. Because the significance of r depends on the sample size, and because the minor group sample is often much smaller than the major sample, some investigators (e.g., Kirkpatrick et al., 1968, p. 132) using the improper method have concluded there was bias when the r was not significantly greater than zero in the minor group, even though the r was exactly the same in the major and minor groups!

Rejection and Nonrejection of the Null Hypothesis. The proper strategy is, first, to determine if the null hypothesis of no bias can be rejected at a given level of confidence, and, second, to assess the practical consequences if the null hypothesis is rejected.

If the null hypothesis is not rejected (i.e., if there are nonsignificant differences between the major and minor groups in the slopes, intercepts, and standard error of estimates of the regression of criterion measures on test scores), one cannot conclude that the test is biased. But this may be a strong or a weak conclusion depending on the sample sizes involved and hence of the power of the study for rejecting the null hypothesis.

There is fortunately a simple and clear-cut procedure in this case for determining whether the study is in fact capable of rejecting the null hypothesis if it is false. The method consists simply of reversing the predictor (e.g., test scores) and criterion variables and testing the significance of the difference between the major and minor groups in the regression parameters for the regression of test scores on the criterion measures. If the correlation between test scores and criterion is less than perfect in both the major and minor groups, which is always the case in reality, and the groups differ in means, then, if the regression of the criterion on test scores is the same in the two groups (i.e., no bias), the regression of test scores on the criterion cannot be the same for both groups. If the intercepts are the same for both groups in predicting from test to criterion, they will necessarily differ between groups when predicting in the other direction. If a study cannot reject the null hypothesis of no difference for the regressions in either direction, the verdict is clear: the study is not statistically strong enough adequately to test the null hypothesis. (It is rare in applied statistics that we have such a clear-cut objective criterion for determining whether a study is or is not adequate to test the null hypothesis.) Thus a statistical test of the null hypothesis with respect to bias, strictly speaking, can clearly have one of three decision outcomes: accept, reject, or moot. Unfortunately, no studies, to the best of my knowledge, have explicitly recognized the third category of decision.

Statistical rejection of the null hypothesis, provided that there is a true nonzero difference, however small, between the groups in the population, can always be accomplished simply by increasing the sample size sufficiently. The question, then, is whether the difference is so small as to be trivial in terms of any practical use of the test. If the difference is so small as to be trivial, the test can be treated as unbiased for all practical purposes, even though the hypothesis of no bias has been statistically rejected. The answer to that question will depend on the available alternatives to use of the test. How valid and unbiased are other available predictors? Is the error of prediction introduced by treating the test as if it were unbiased (i.e., by using a common regression line for the major and minor groups) greater than the sampling error incurred by using a separate regression equation for the minor group if the regression parameters are based on a much smaller sample than are the parameters for the major group? Finally, in which group is the criterion performance underpredicted, and by how much? In most cases, these group errors of prediction due to a biased test can be minimized or eliminated altogether when using the test for selection by entering the test scores along with group membership in a multiple regression equation. (See the discussion of the Multiple Regression Model in Chapter 9.)

Test Bias in Predicting Scholastic Performance

Elementary School. The published evidence here is surprisingly meager, probably for two main reasons: (1) because tests are not generally used for selection in the elementary grades (1 to 8), there has been little concern with their predictive validity, as compared with, say, college and vocational aptitude tests; and (2) teachers’ marks in elementary school are not a very solid criterion for studies of predictive validity.

Nevertheless, the few available studies suggest that standard IQ tests have quite comparable validities for blacks as for whites in elementary school. Sattler (1974, pp. 43-44) has reviewed some of this evidence. A study of 1,800 black elementary school children, ages 5 to 16, in the southeastern United States showed a correlation of .69 between Stanford-Binet MA and California Achievement Test Scores and .64 to .70 with grades in academic subjects, but only .32 with overall teacher ratings. In other studies the Stanford-Binet correlated .67 with the Metropolitan Achievement Test in a disadvantaged sample, ages 8 and 11, of whom 80 percent were black. Stanford-Binet also correlated .57 with the reading achievement of second- and third-grade black boys. There are significant correlations ranging from .38 to .61 between the WISC and the Wide Range Achievement Test in samples of 6-year-old white and black children. None of these findings is very informative, but they do indicate that significant validities of about the same magnitude as are generally found in the white school population are also found in the black.

Thorndike (1971b) provides comparative data on the validity of the Lorge-Thorndike Verbal and Nonverbal IQ for white and black pupils in one Maryland county. (See Table 10.1.) Thorndike remarks:

Correlations do average somewhat lower for black students, reflecting in part smaller variability in this black group of students, but the correlations clearly follow much the same pattern and are of the same order of magnitude. The abilities needed . . . to master academic materials know no color line. Reading, science, mathematics make the same demands on blacks as on white students. The same abilities are needed to cope with them in either case. (1971, p. 1)

A study by Crano, Kenny, and Campbell (1972) gives predictive validities of the Lorge-Thorndike total IQ for large samples of inner-city (N = 1,499) and suburban (N = 3,992) school children. The correlation of IQ obtained in Grade 4 with a composite score on scholastic achievement tests (Iowa Test of Basic Skills) obtained in Grade 6 was .73 for the suburban sample and .61 for the inner-city sample. The significant difference found between these correlations cannot be interpreted from the evidence given, and we cannot determine whether the different correlations result in significantly different regressions in the two groups. For making these evaluations we would need to know the groups’ means, standard deviations, and reliabilities of both the IQs and achievement scores. Unfortunately this information is not provided by Crano et al.

The appropriate regression statistics, however, were obtained in a recent study of the validities of verbal and nonverbal IQ tests for predicting scholastic performance as indexed by grade point average (GPA) in large samples of elementary school children in England (Messe, Crano, Messe, & Rice, 1979). The data were analyzed separately in high, middle, and low SES samples. The predictive validity coefficients average about 0.60 and do not differ as a function of SES. The regressions of grade point average on IQ, determined separately in the low, middle, and high SES samples, do not differ significantly in standard error of estimate or in slope, but they do show a slight but significant intercept bias. IQ significantly overestimates GPA in the low SES sample and significantly underestimates GPA in the middle SES sample. That is, the predictive bias of the IQ “favors” the lower SES children.

Jensen (1974d) examined the validity of a number of ability, socioeconomic, and personality variables (eleven in all), in addition to sex, age, and ethnic group membership for predicting scholastic achievement (Stanford Achievement Test) in various school subjects (eight in all) in Grades 1 to 8 in California schools comprised of whites (N = 2,237), blacks (N = 1,694), and Mexican-Americans (N = 2,025). The predictor measures were obtained at the beginning of the school year and the achievement tests at the end.

The predictive validity (multiple R) of this battery in the combined groups ranged from .60 to.80 for various school subjects, in different grades, with an overall average validity of R = .70. The Lorge-Thorndike IQ contributed by far the most of this multiple correlation. The validities steadily and markedly increase going from the first to the eighth grades.

But the more important point of this study is that overall the addition of ethnic membership to the thirteen other predictors in the multiple regression equation does not add a significant increment to the R, despite the large sample sizes. If the battery of predictor variables was biased with respect to any of these ethnic groups, we should expect the addition of ethnicity as a predictor variable to significantly enhance the R. But in fact the independent contribution of ethnicity was generally negligible. For example, the average point-biserial correlation between ethnicity and achievement was .522 for white-black and .314 for white-Mexican. When the thirteen predictor variables were partialled out of these correlations, they dropped to nonsignificant values of .055 (p = .379) and -.083 (p = .237), respectively. In other words, the contribution of pupils’ ethnic group membership to the prediction of scholastic performance, independently of psychometric, personality, and status variables, was practically nil. Thus, with a good choice of predictor variables, such as were used in this study, it is possible to predict scholastic achievement in the elementary grades with considerable validity (about .70) for white, black, and Mexican-American children without having to take their ethnicity into account.

High School. ... Farr et al. (1971) studied the validity of the California Test of Mental Maturity (CTMM), a widely used IQ test, in ninth- and twelfth-grade racially integrated classes in North Carolina public schools. Unfortunately, the samples are not very large: ninth grade, 166 whites and 55 blacks; twelfth grade, 245 whites and 58 blacks. The criteria were teachers’ grades in English, math, science, social studies, and total GPA. Also, teacher ratings were obtained on leadership (class participation, initiative, dominance, acceptance by others, etc.) and creativity (generalization of new ideas, seeks new solutions, independence, originality, interest in outside activities, etc.). Twelfth-graders were also assigned a “rank in class” for academic performance (position divided by class size).

Whites and blacks in the ninth grade differed an average of 12.2 IQ points (or .84σ in terms of the within-groups standard deviation); the average racial difference in the twelfth-grade sample was 17.4 IQ points (or 1.37σ). Whites and blacks differed less in overall GPA: .58σ in the ninth grade and .69σ in the twelfth grade. This is a general finding in many other studies: blacks and whites differ somewhat less in school grades than in IQ or in objective test measures of scholastic achievement. Table 10.2 shows the correlations between CTMM IQ and teachers’ grades and ratings. The black and white regressions also were compared on each of these variables. The type of bias, in terms of the Bartlett-0’Leary models (see Chapter 9, pp. 390-391) is indicated in the column headed “Model.” Model 1 represents “no bias,” that is, nonsignificantly different slopes and intercepts in the two groups. Model 2 represents intercept bias, with the whites having the higher intercept, thus resulting in underprediction of the criterion for whites and overprediction for blacks when the common regression (based on the combined groups) is used for prediction. In Grade 9 only science grades show this type of bias. The CTMM predicts all the other measures without slope or intercept bias. In Grade 12, the Bartlett-O’Leary model 8 is represented in both English and science grades and in leadership ratings. In model 8 the predictor is valid for whites but not for blacks, and there are significant mean differences on both the predictor and the criterion. In Grade 12, the predictive validity of the CTMM for math grades was nonsignificant in both groups. But in both grades the CTMM IQ predicted the overall GPA without bias as well as rank in class for twelfth-graders. In the four (out of fifteen) comparisons that showed significant bias, in every case it would “favor” the black groups, that is, the use of the white regression line or the common regression line for all students would result in overprediction of the blacks’ criterion performance. ... In those cases where predictive bias is found, the use of the majority regression line or the common regression line almost invariably favors blacks relative to whites.

Although the study tested for bias in slopes and intercepts, it did not compare the standard error of estimates in the white and black groups. So I have done this, using the data provided by the authors. Significantly different standard error of estimates indicate that the predictions for the two groups are of unequal reliability; that is, they do not involve equal risk of errors in prediction. There are four instances in which the standard error of estimates differs significantly at the .05 level (as indicated by a superscript b in the “Model” column of Table 10.2); in each instance, the standard error of estimate is larger for the white group - that is, errors of prediction are greater for whites than for blacks. But the only two criteria, out of a total of eight, for which there is any significant predictive bias of any kind at both grade levels is for grades in English and in social studies.

A related study by Fox (1972) involved more than 11,000 ninth- and twelfth-grade students of both races in thirty-nine high schools from nine districts in North Carolina, representing a stratified random sample of North Carolina high school students. It shows the correlation of CTMM IQ with items of a biographical inventory that discriminate significantly between the races. A random half of the total sample (N = 5,524) was given an inventory of three-hundred questions (with from three to five multiple-choice answers) concerning a great variety of biographical information. The items that discriminated beyond the .01 level of confidence between the races were then cross-validated in the other random half of the sample (N = 5,524), and only the items that discriminated significantly in the second sample were retained. It is noteworthy that a total of only forty-nine of the three-hundred biographical items significantly differentiated race (white versus black) for males (twenty-seven items), females (thirty-six items), or both sexes (twenty-three items). One might expect the items of a biographical inventory to be much more “culture loaded” than the items of an IQ test, and yet only about 8 to 16 percent of the three hundred biographical items discriminated significantly between the races. Yet, even though intelligence test items are not selected in terms of racial criteria, virtually all the items of standard group IQ tests discriminate significantly between whites and blacks in samples of comparable size to those used in the present study. Apparently, in a broad catalog of life experiences, whites and blacks do not differ as much as many would imagine. Of course, none of the biographical items pertain to race per se, but they do pertain to socioeconomic factors, family size, parental education and occupation, interests, values, likes and dislikes, and a great variety of social and cultural experiences.

The finally selected items were keyed so that higher scores were indicative of white biographical experiences. Scores on the Biographical Race Key in the total sample have a point-biserial correlation with actual racial classification (black = 1, white = 2) of .56. (This corresponds to a mean white-black difference on the Biographical Race Key of approximately 1.35σ.) The correlations (curved lines) and partial correlations (straight lines) shown in Figure 10.1 are of particular interest. The point-biserial correlation of .45 between race and IQ corresponds to a mean difference of approximately 1σ or 15 IQ points. Notice that, when the racially differentiating biographical factors are partialed out of this correlation, it drops from .45 to .27, indicating that IQ measures some substantial difference between the races that is wholly independent of those life experience differences between the races assessed by the biographical inventory. However, one cannot prove from such correlational data that any part of the race correlation with IQ is caused by the biographical differences. We can say only that the CTMM IQ reflects something more than just these biographical differences.

Note, too, that biography is correlated .27 with IQ after race is partialed out, which means that there is a correlation between IQ and the biographical factors within each racial group. Finally, much of the biographical variance is associated with race independently of IQ, as indicated by the partial correlation of .45. Those who argue that all the racial IQ variance merely reflects differences in life experience, values, and attitudes, such as are tapped by the biographical inventory, should be able to devise a biographical inventory on which the correlation of race and IQ (with biography partialed out) is nonsignificantly different from zero. The obtained correlation of .45 between race and IQ thus would have to be accounted for through the indirect effects of race on biography and of biography on IQ, which requires that the product of the partial correlations race X biography (partialing out IQ) and biography X IQ (partialing out race) must equal .45. This would obviously call for a biographical inventory having a very much higher partial correlation either with race or with IQ (or both) than does the present inventory. If such an inventory could be devised, it would be instructive to examine its item content. Would it reflect the kinds of cultural learning experiences that some critics claim make IQ tests racially biased?

Comparisons of Predictive Test Bias in Various Ethnic Groups. Although the well-known Coleman report, Equality of Educational Opportunity (Coleman et al., 1966), made no attempt to examine test bias, it provides massive data ... from which we can make such an examination. This nationwide survey of scholastic aptitudes and achievements involved the testing of more than 645,000 children in 4,000 public schools, which constitutes the largest school testing program ever undertaken using a common battery of aptitude and achievement tests. Children were tested only in grades 1, 3, 6, 9, and 12, and larger numbers of various minorities were included than their proportions in the population, to ensure adequate-sized samples for the many statistical analyses required in this study. The sample sizes are so large, in fact, that the sampling error of almost any descriptive statistic based on the Coleman samples is practically negligible.

In Grades 3, 6, 9, and 12, both verbal and nonverbal aptitude tests were given, as well as scholastic achievement tests in reading comprehension and mathematics. Grades 9 and 12 were also given a test of general information, consisting of ninety-five items on such diverse subjects as practical arts (tools, automobiles, building, food, sewing, decorating, etc.); natural science; literature, music, and art; and social science (history, government, public affairs). The scholastic achievement tests are made up of standard tests produced by the Educational Testing Service and are typical of the standardized achievement tests used by most school systems. The verbal and nonverbal aptitude tests are taken from standard group tests of verbal and nonverbal IQ and are highly typical of most such group IQ tests used in schools, involving items such as picture vocabulary, picture association, classification, sentence completion, and figural and verbal analogies.

Table 10.3 shows the amount by which each of the minority groups deviates from the white majority mean on each of the tests; the mean difference is expressed in units of the white standard deviation on the particular test at the given grade level.

We can determine the degree of predictive bias in these typical verbal and nonverbal “IQ” tests for various minority groups by seeing how accurately scores on these ability tests can estimate (or “predict”) the mean performance of various minority groups on the achievement tests, basing the estimate on the regression equation derived from the white majority. [2] The estimated means for the minority groups can then be compared with their actually obtained means on the achievement tests. The amount of the discrepancy (D) between the estimated mean (Y^‾) and the obtained mean (Y‾), expressed as a proportion of the total standard deviation (σ) of the achievement scores for the particular group in question, that is D = (Y^‾ - Y‾)/σ, is an index of the amount of predictive bias of the IQ test. A positive value of D indicates overprediction of the criterion; that is, in using the prediction equation derived from the white majority to predict the mean achievement test score of the minority group, the aptitude test (verbal or nonverbal IQ) predicts a higher mean on the criterion measure (achievement test) than was actually obtained.

The results of this analysis are shown in Table 10.4 for blacks, Mexican- Americans, American Indians, and Orientals (Chinese- and Japanese-Americans). To gain some idea of how much of the predictive discrepancy (D) might be attributed solely to test unreliability, another value, labeled Dc, has been calculated to show the estimated value of D if the tests had perfect reliability. This is achieved simply by correcting the regression equation for attenuation, [3] assuming that the actual reliability of all of the tests is .90, which is a typical reliability coefficient for most standard group tests of IQ and scholastic achievement. Because the Coleman report provides no information on the reliability of these tests in the various groups, the calculation of Dc based on the reasonable assumption of a test reliability of .90 in all samples is done merely to illustrate in a general way the approximate effect of correcting the regression equation for attenuation (i.e. test unreliability). The effect, in general, is to decrease the amount of overprediction by about .07σ.

As can be seen in Table 10.4, the minority group means on the criterion tests are generally overpredicted by the IQ tests, using the regression equation based on the white majority pupils. Blacks evince the largest degree of overprediction, Orientals the least, with Mexican-Americans and Indians intermediate. Except for Orientals, the amount of predictive bias (i.e., overestimation of minority achievement test means) is considerable, amounting to as much as half a standard deviation or more in some instances. In other words, the verbal and nonverbal IQ tests tend to overestimate the mean level of reading comprehension and mathematics achievement and general information of the minority pupils. That is, white pupils with the very same IQ scores as the mean IQ of a minority group actually obtain higher achievement scores. This finding is just the opposite of the popular notion that the usual IQ tests are biased so as to underestimate the actual scholastic performance of minority pupils.

Notice also that the verbal IQ shows less predictive bias than the nonverbal IQ, and this is true even for the minority groups in which bilingualism is most common. This finding, too, goes counter to popular expectations. The reason for it is that verbal IQ has considerably higher validity than nonverbal IQ for predicting scholastic achievement and general information within every ethnic group. In a factor analysis, scholastic achievement scores are highly loaded not only on g but also on a verbal ability factor measured in the language of instruction in the school.

It should be remarked that the predictive bias might be lessened considerably if the verbal and nonverbal IQ tests were combined in a multiple regression equation instead of being used separately in simple regression equations as was done in Table 10.4. Our purpose here, however, was not to determine the maximum predictive validity that could possibly be obtained from these particular tests, but to determine the direction of the predictive bias of typical verbal and nonverbal aptitude tests in the various minority groups. [...]

The validity of the Wechsler Intelligence Scale for Children (Revised) (WISC-R) for predicting scholastic achievement in reading and math (as measured by the Metropolitan Achievement Tests) was investigated by Reschly and Sabers (1979) in a stratified random sample of children from four ethnic groups in the schools of an Arizona county with a large urban population. Pupils were selected in equal numbers from Grades 1, 3, 5, 7, and 9. The four ethnic groups were whites (called Anglos), blacks, Mexican-Americans, and Indians (Native American Papago). The predictor variable was the WISC-R Full Scale IQ; the two criteria were the reading and math scores of the MAT.

The regressions of the criterion scores on the predictor scores were compared simultaneously across the four ethnic groups at each grade level by means of the Gulliksen-Wilks procedure, which tests sequentially for significant differences in standard error of estimate, slope, and intercept. The hypothesis of the same regression equation for all groups was rejected at the .05 level at every grade, for the prediction of both reading and math. Most of the significant differences were differences in intercepts. Thus by this stringent statistical criterion the WISC-R is an ethnically biased predictor of reading and math achievement.

So we must go on to examine the direction and magnitude of the predictive error when the common (i.e., based on the combined groups) regression equation is used for each ethnic group, to gain some idea of the practical consequences of the predictive bias for each group. This is given in Table 10.5, in which I have averaged the authors’ results over grades, since there appears to be no systematic effect of grade level for those statistics. First, note the validity coefficients (i.e., the Pearson correlation between the Full Scale IQs and the MAT scores); only the Papago Indians show appreciably lower values than the other three groups, which differ only slightly. The deviations of the predicted achievement scores from the actual achievement scores are expressed in units of each subgroup’s own standard deviation. It can be seen that these discrepancies between predicted and obtained scores are quite small and statistically nonsignificant for all groups except the Indians, whose actual achievement is significantly overpredicted by the WISC-R IQ. At the other extreme, the Anglo group’s actual achievement is slightly, but not significantly, underpredicted by the common regression equation. For practical purposes, this small amount of bias, except for the Indians, would hardly justify the use of separate regression equations for each group. The WISC-R Full Scale IQ appears to have very much the same meaning for white, black, and Mexican-American pupils in relation to their achievement in reading and math.

Predictive Bias in the Armed Forces

Level I and Level II Types of Tests. How can we account for this difference? The best hypothesis, I would suggest, is that the difference in the two types of regression bias found in college and in the armed forces is the result of a difference in the factorial composition of the criterion measures. In extensive studies, we have found that the regression of relatively simple learning and memory measures on highly g-loaded measures (such as IQ, SAT, AFQT, and GCT) differ in whites and blacks in exactly the same way that the regressions of armed forces training final grades on AFQT or GCT scores differ in whites and blacks. Figure 10.4, for example, shows the regression of scores on a simple memory for numbers test on Lorge-Thorndike nonverbal intelligence test raw scores in large samples of white and black school children (Jensen, 1974b). Notice how similar these regressions are to those in Figures 10.2 and 10.3. There generally seems to be less difference between whites and blacks on performance involving rote learning and memory (which I have labeled level I ability), than on tasks involving abstract conceptual ability (level II ability); also, level I and level II abilities are slightly less correlated in blacks than in whites (Jensen, 1974b). I conjecture that the content of most armed forces training courses involves relatively more level I ability than the content of academic courses in college, and this results in the differing slopes of the white and black regression lines. College GPA, in contrast to final grades in armed forces training schools, is probably almost as highly loaded on level II ability (after correction for attenuation) as are the predictor tests.

How serious is the degree of bias in the AFQT and GCT as shown in Figures 10.2 and 10.3? The Gulliksen-Wilks (1950) chi squared test of the significance of the difference between the white and black regressions shows that, even with these very large samples, the standard error of estimates do not differ significantly, which means that errors of prediction are essentially no different for the two groups when prediction is based on each group’s regression line. The slopes, however, differ very significantly. (A test of the intercept difference is uncalled for when the slopes differ significantly.) If the white regression equation were used for predicting the final school grades of blacks, it would rprcdict for low-scoring blacks and overpredict for high-scoring blacks on both the AFQT and GCT. At the points of over- or underprediction of the final school grade the average error of prediction amounts to slightly less than one-fourth of the white standard deviation for the GCT and one-sixth of a standard deviation for the AFQT. The final school grade means of whites and blacks differ by .37σ. Thus the largest average errors of prediction of black grades, using the white regression equation, are relatively large, so that it would be advisable to use separate regression equations for blacks and whites or to include the quantitized racial dichotomy and its interaction with test scores as a moderator variable in a multiple regression equation for predicting final school grade.

I venture the generalization that slope bias will be manifested in black-white regression comparisons whenever the criterion involves a much less g-loaded type of performance than the predictor test. In other words, highly g-loaded cognitive tests are very likely to show slope bias in black-white comparisons when the criterion performance to be predicted includes a large component of level I memory ability or is relatively lacking in level II abstract-conceptual ability. The best remedy for this condition is to include other less g-loaded but criterion-correlated variables in the prediction equation, along with race as a moderator variable, as explained in Chapter 9 (pp. 417-418).

We see this generalization demonstrated again in a sample of marine corps recruits undergoing training in Service Support Schools for several relatively low g-loaded jobs: food service, supply, and transport personnel (Farr et al., 1971, pp. 85-97). The training course lasted less than three weeks. There were ninety-nine whites and eighty-four blacks. The white-black mean difference on the predictor test (AFQT) was .94σ, which is significant beyond the .01 level. The white-black mean difference on the criterion measure (class standing) was only .35σ, which is quite nonsignificant (t = 0.25). The correlation between AFQT and class standing was .47 (p < .01) for whites and .05 (n.s.) for blacks (a significant difference in validities). The slopes of the white and black regression lines differ significantly (p < .05). It is instructive to compare the regression on another predictor test that is less conceptually complex than the AFQT, namely, the Fundamental Achievement Series (FAS), which is a test of elementary verbal and numerical skills. On this simpler test the white-black difference was only .72σ (as compared with .94σ on the AFQT). The correlations of FAS with class standing were .30 and .11 for whites and blacks, respectively; and, although the white-black slope differences were in the same direction as for the AFQT, they were of nonsignificant magnitude.

Another study (Farr et al., 1971, pp. 114-149) complements the previous study in its consistency with our level I-level II hypothesis. This study involves forty-six white and forty-eight black sophomore students at the University of Maryland who took part in an experiment specially designed to test an aspect of the level I-II hypothesis. The students undertook a five-hour unit of programmed instruction in elementary statistics. This subject matter is quite abstract and conceptual.

The criterion measure in this training unit was a thirty-item multiple-choice achievement test designed to measure applications of concepts and principles to new situations which were not included in the programmed instruction. This criterion test, therefore, is a highly g-loaded level II measure. Two main criterion measures were used: posttest scores and residual gain scores (i.e., the difference between actual posttest scores and the predicted posttest score as predicted from the pretest score on the thirty-item achievement test).

The predictor variables of particular interest were two level I tests - memory span for numbers and paired-associates learning (ten nonsense syllable/common noun pairs) - and a measure of level II or general intelligence (Wonderlic Personnel Test). The mean white minus black differences (in standard deviation units) and their two-tailed significance levels are

Level I tests   – Memory for Numbers                      +0.37σ, p > .05
–                      – Paired Associates                             -0.39σ, p > .05
Level II tests – Wonderlic Personnel Test               +1.70σ, p < .001

The mean white minus black differences (in σ units) and their significance levels on the criterion measures are

Pretest achievement scores                                       +1.30σ, p < .001
Posttest achievement scores                                     +1.27σ, p < .001
Residual gain                                                               +0.78σ, p < .001

The validity coefficients of the predictor tests are shown in Table 10.6.

None of the validity coefficients in Table 10.6 differs significantly between whites and blacks. Only the Wonderlic showed significant validities, except for predicting the blacks’ residual gain score, which was nonsignificant (p > .05). As for the regressions, the two level I predictors (Memory for Numbers and Paired Associates) both showed significant (p < .01) intercept bias but no slope bias. On these tests the differences between the standard error of estimates for whites and blacks is nonsignificant or of borderline significance (.05 < p < .10). Marked white-black differences between intercepts but not slopes has been found in other studies involving the regression of level II measures on level I measures. For example, Figure 10.5 shows the regression of Lorge-Thorndike Nonverbal Intelligence Test raw scores on Memory for Numbers scores in a large sample of black and white children in Grades 4 to 6. In summary, it appears that when a level II test is used to predict level I performance, there is mainly slope bias (Figure 10.4); and when a level I test is used to predict level II performance, there is mainly intercept bias (Figure 10.5). The Wonderlic Personnel Test, a level II predictor of the level II criterion, shows no significant white-black difference in slopes or intercepts. The standard error of estimate of the posttest scores, however, is slightly but significantly (p < .05) larger for whites, due to the greater variance and lesser validity of whites on this criterion measure.

What is the main practical consequence of the generalization noted, namely, that g-loaded or level II tests tend to show slope bias (with whites having the steeper slope) when predicting a performance criterion that is considerably less g loaded than the test? A good indication is to be found in a large-scale study of U.S. Navy trainees in Class A training schools for twenty-five various specialized jobs in the navy (Thomas, 1975). There was a total of 50,618 white and 2,239 black students. Final grades in the twenty- five training courses were predicted from a composite score consisting of the simple sum of two or three tests (including the General Classification Test in all but three courses) of the navy’s Basic Test Battery consisting of the GCT and more highly specialized tests: Mechanical Knowledge and Comprehension, Shop Practices, Arithmetic Reasoning, and the Electronics Technician Selection Test (math, science, electricity, and radio knowledge). Adding one or two of the specialized tests to the GCT generally increases the predictive validity and reduces regression biases by increasing the similarity of ability factors common to both the predictor and criterion variables. Using these composite predictors, Thomas found one or another form of white-black regression bias in the prediction of final grades in thirteen out of the twenty-five courses. The equality of standard error of estimates, slopes, and intercepts were tested sequentially by the Gulliksen-Wilks chi squared test. There were nine courses for which the regressions showed a significant (p < .05) racial difference in standard error of estimates (blacks having larger standard errors of estimate in eight out of the nine courses); three courses with a significant difference in slopes (whites having a steeper slope in all courses); and one course with a significant difference in intercepts (whites higher). Because Thomas gives the minimum qualifiying score on the predictor variable for assignment to each of the twenty-five navy class A schools, we can determine whether the selection bias in those cases showing significantly different regressions “favors” whites or blacks when the white regression equation is used. In every one of the thirteen courses with significantly unequal regressions, the bias “favors” the black selectees (i.e., the tests overpredict) the blacks’ final course grades. The reason is that the white and black regression line is above the black regression line; and in those cases where the regression lines are parallel, the white is above the black (i.e., intercept bias). In many cases, the amount of bias, though statistically significant with these large samples, is practically trivial. In every case, the bias is always in the direction of overpredicting the average final grades of the black students who test above the minimum qualifying score.

AFQT and Job Knowledge versus Job Sample. A study of the differential validity of the AFQT for predicting scores on an objective test of job knowledge as compared with scores on an objective measure of performance on a job sample (i.e., actually performing certain aspects of the job itself) showed that the AFQT overpredicted blacks’ job-knowledge scores more than their job-sample scores (Caylor, 1972). The four army job categories do not make very highly g-loaded demands: cook, mechanic, armor crewman, and supply specialist. Groups of whites and blacks in these jobs, matched on AFQT scores and number of months on the job, were compared on measures of job-knowledge and job-sample performance. The mean AFQT scores of these groups are quite low, falling into mental category IV. The average correlations between AFQT and job-knowledge scores were .47 for whites and .29 for blacks; correlations between AFQT and job-sample scores were .37 for whites and .20 for blacks. The AFQT is not an impressive predictor of job performance for either of these rather low-ability groups. But, again, we see that a predominantly g-loaded variable, the AFQT, shows appreciably lower correlations with much less g-loaded criterion variables for blacks than for whites. For both groups the AFQT predicts job knowledge better than it predicts job performance. Thus, it is apparent that verbal knowledge about a job and actually doing the job involve somewhat different ability factors. In the white and black groups matched on AFQT and months on job, the whites averaged a significantly (p < .05) .125σ higher than blacks on job-knowledge scores, but were only a nonsignificant .033σ higher on job-sample scores. Thus the AFQT appears slightly biased (overpredicting blacks’ scores) on job knowlege but not on job performance. [...]

Bias in the Test Prediction of Civilian Job Performances

Single-group Validity and Differential Validity. ... Single-group validity is demonstrated when one group shows a validity coefficient significantly larger than zero and the other group does not. Differential validity is demonstrated when the two groups’ validity coefficients differ significantly from one another. It must be emphasized that single-group validity and differential validity are independent; the latter cannot be inferred from the former, even when sample sizes are equal.

Boehm (1972) reviewed thirteen studies reporting single-group and differential validities in white-black comparisons. [5] The thirteen studies involved such occupations as medical technicians, telephone craftsmen, clerical workers, general maintenance, heavy vehicle operators, toll collectors, office personnel, machine shop trainees, administrative personnel, psychiatric aides, and welders. The studies employed a total of fifty-seven various predictor tests and thirty-eight criterion measures based mostly on supervisor’s ratings of job performance or, less frequently, objective job knowledge and job sample tests. The average numbers of subjects per study were 135 whites and 101 blacks. The studies yielded altogether 160 white-black pairs of validity coefficients, which can be classified as follows:

–                                                                                Number      Percent
Nonsignificant validity in both groups                 100              62
Significant (p < .05) validity in both groups         27               17
Significant validity for whites only                         20               13
Significant validity for blacks only                         13                 8
Significant differential validitv                                7                 4

Single-group validity is a logically inappropriate indicator of test bias, as pointed out near the beginning of this chapter, so the only important finding in the preceding table, in terms of our inquiry, is differential validity, of which there were only 7 cases out of a possible 160, or 4 percent. But the number of differences significant at the .05 level expected by chance is 8. Thus these thirteen studies overall lend no support to the claim that tests are differentially valid for whites and blacks. It also appears that the findings of single-group and differential validity are closely linked to sample size. The more adequate the sample sizes in both groups, the less likely the appearance of single-group or differential validity. In none of the studies where N exceeded 100 in both white and black samples was there found any instance of either single-group or differential validity. Also, when the validity coefficients were determined for the combined white and black samples in each of the 120 instances where this information was given, in only 3 instances was the total group validity coefficient less than the validity for either racial group alone. In 117 (or 98 percent) of the cases, the combined-groups validity coefficient lies above or between those of the separate groups. This is statistically consistent with the hypothesis that the validities are the same in both populations, which, however, differ in central tendency on both the predictor and criterion variables. [...]

The evidence from the thirteen studies reviewed by Boehm (1972) leads one to hypothesize that with respect to white-black comparisons single-group validity is statistically artifactual and differential validity is a rare, or even nonexistent, phenomenon. Schmidt, Berner, and Hunter (1973) tested this hypothesis. They set up a “null model,” hypothesizing that the test’s validity coefficient is exactly the same for the white and black populations but would show single-group validity in various sample comparisons as a result of the absolute sample sizes of whites and blacks, the difference in sample sizes, and the overall average level of validity. Using this statistical model, which assumes no difference in the true population validity for blacks and whites, they then predicted the outcomes of nineteen studies of employment test validities in white and black samples, involving a total of eighty-six different predictors of seventy-four different criterion measures. (Twelve of the nineteen studies were the same as those included in Boehm’s review of thirteen studies. [6]) There was a total of 410 white-black pairs of validity coefficients, which were classified as follows, with the percentages of the observed and the predicted outcomes in each category. The null model predicts the empirical outcomes very well indeed, as shown by the fact that the differences between the observed and predicted percentages do not even approach significance [χ² = 1.39, n.s. (p > .80)].

–                                                                            Observed     Predicted
Nonsignificant validities in both groups           59.5%         57.0%
Significant validities in both groups                  12.9             15.5
Significant validity for whites only                    18.3             18.4
Significant validity for blacks only                      8.3               9.1

Schmidt, Berner, and Hunter also classified the validity coefficients into those based on subjective criteria (e.g., supervisor ratings) and those based on objective criteria (e.g., job-knowledge and work-sample tests), to see if their null model predicted the validity outcomes as well for both types of validity criteria. For both types, the frequencies of the observed and predicted outcomes do not differ significantly (p > .20 and p > .50 for subjective and objective criteria, respectively). The authors conclude:

A conservative interpretation of these findings is that they cast serious doubt on the existence of single-group validity as a substantive phenomenon. The close fit of the null model likewise indicates that differential validity - which is much less frequently reported in the literature - is probably illusory in nature, (p. 8)

Regression Studies. Studies of the homogeneity of regressions are, of course, the most valuable method for assessing test bias. Fortunately, there are now numerous studies that use this method on employment selection tests comparing whites and blacks.

Ruch (1972) reanalyzed twenty such validity studies of paper-and-pencil tests in the literature that met the following criteria: [7]

1. Studies were conducted in a business or industrial (i.e., noneducational, nonmilitary) setting. 2. Separate statistics were available for blacks and whites. 3. Race was not confounded with some outside variable that would preclude meaningful interpretation. 4. Necessary data were reported to enable a test of homogeneity of regression between racial groups.

A variety of paper-and-pencil aptitude tests and a variety of job performance criteria were employed in these twenty studies, often several in one study. Thus there were altogether 618 white-black pairs of regressions to be statistically compared.

Ruch used the Gulliksen-Wilks (1950) method of testing the homogeneity of regressions between blacks and whites. This method sequentially tests for significant differences in standard error of estimates, slopes, and intercepts, in that order, and rejects the null hypothesis of homogeneity of regressions on the first parameter of the regression that shows a difference significant at the 5 percent level.

Of the 618 tests of significance between standard error of estimates, 72 (12 percent) were significant; of the remaining 546 tests for slopes, 64 (12 percent) were significant; and of the remaining 482 tests for intercepts, 87 (18 percent) were significant. There were altogether 395 (64 percent) pairs of regressions that showed no significant difference in standard errors, slopes, or intercepts. If there were really no significant differences between the populations, then, by chance, we should expect to find 530 (86 percent) that are nonsignificant at the 5 percent level, but only under the assumption that the 618 pairs of regressions are all derived from independent samples. Because many, however, were based on the same black and white samples, they are not statistically independent, and thus we cannot determine directly from these figures whether there are more significant differences than would be expected by chance. Ruch tried (incorrectly) to get around this problem by counting the number of significance tests in each study for each regression parameter that showed significance at p < .05 and determining whether that number was greater or less than would be expected by chance under the null hypothesis. Unfortunately, this does not solve the problem, because the significance tests within a given study do not involve independent samples, and the various predictor variables are highly intercorrelated as well as are the various criterion measures. So we really have no way to estimate how many significant differences would be due to chance if the null hypothesis is true. Statistical logic forces us to give up any hope of answering that question.

However, it is worth noting that in all twenty of these studies, not a single one shows biases for any given regression parameter that go in opposite directions for blacks and whites for different pairs of predictors and criteria. For example, if the regression lines for one pair of predictor criterion measures shows a significantly small slope for blacks, a significantly greater slope for blacks is never found for any other pair of predictor criterion measures used in that study. The same thing is true for standard error of estimates and for intercepts. This fact merely reflects the high degree of correlation that must exist among the predictor variables and among the criterion variables. Therefore, I believe that the best way to summarize all the results of these twenty independent regression studies is by the following procedure. In each study, for each regression parameter (i.e., standard error of estimate, slope, and intercept), there is one of three possible outcomes of the statistical test of the significance of the difference between blacks and whites: (1) nonsignificant (p > .05), (2) white significantly (p < .05) larger than black (W > B), and (3) black significantly (p < .05) larger than white (B > W). Thus, for each study, we can determine which of these three possible outcomes occurs at least once for each parameter among all of the regressions computed between the various predictor and criterion variables used in the study. Notice that each study is counted no less and no more than once with respect to each one of the three regression parameters. The tabulations over all twenty studies are shown in Table 10.8. From this information we can ask, Do the biases that are significant tend consistently to favor whites and disfavor blacks over all twenty studies, or is the direction of these biases nonsignificantly different from random, favoring one group about as frequently as the other? If the direction of bias was merely random across all the studies, we should expect no significant differences between the frequencies of W > B and B > W shown in Table 10.8. A chi squared test (with 1 df) shows these differences to be nonsignificant (n.s.) for the standard error of estimate and the slope, but highly significant (p < .01) for the intercept. In other words, there is no evidence across studies of bias in standard error of estimates or slopes of which the effects on selection would consistently favor one group over the other. But there is a highly significant and consistent bias for intercepts, with the common finding of the white intercept being higher than the black. This means that, if the regression equation for whites is used to predict the criterion measure for blacks, it overpredicts the blacks’ average performance. Any selection procedure using the same regression equation for both whites and blacks, therefore, will be biased against white and in favor of blacks. That is the only statistically warranted overall conclusion regarding predictive test bias that can be drawn from the mass of regression data provided by the twenty independent studies included in Ruch’s (1972) review. The remedy for intercept bias, of course, is a statistically simple one: include race (as a quantitized variable) among the predictors in the common regression equation.

Chapter 11 Internal Criteria of Test Bias: Empirical Evidence

Historical Precedents

The Eells Study. [...] In 1946, Eells gave a battery of standard IQ tests to practically all the white pupils of ages 9, 10, 13, and 14, totaling nearly 5,000 children, in a midwestem industrial community of approximately 100,000 population. The test battery included such well-known tests as the Otis, Henmon-Nelson, Thurstone’s Primary Mental Abilities, and the California Test of Mental Maturity. These tests altogether provided more than 650 items on which groups of upper and lower socioeconomic status (SES) could be compared. The index of SES was based on parental education and occupation, type of house, and residential area. On the basis of this index, the sample was divided into three SES levels, labeled high, middle, and low status. The low-status group was further divided into “ethnic” (at least one parent foreign bom, except those from the British Isles, Canada, Germany, and Scandinavia) and “Old American” (both parents American born). Eells demonstrated correlations between IQ and his Index of Status Characteristics that are quite typical of those generally found in such studies, ranging from .20 to .43 for various tests and age levels, which amounts to some 8 to 23 IQ points difference between the high- and low-status groups.

The main analysis consisted of comparing the item difficulties of the more than 650 single test items across the high- and low-status groups and across the ethnic and Old American groups.

Eells’s findings can be summarized in five main points.

1. Status differences vary across test items. The percentage passing each item was transformed to a normalized index of difficulty, thereby representing item difficulty on an interval scale, separately for each status group. All high-low status comparisons on items are based on the difference between the indexes of item difficulty of the high- and low-status groups (i.e., high minus low). These status differences in the index of difficulty for 658 items were found to be roughly normally distributed. It is difficult to say how widely the items vary in showing status differences, as we have no a priori expectation of the amount of variation against which we could compare the amount of variation actually found. (In this regard it would have been much more informative if Eells had matched high- and low-status pupils for total raw score on the tests and then looked at status differences on the individual items.) But the coefficient of variation (CV = 100σ/mean) of the distribution of status differences in the index of item difficulties is 70.5 for 9- and 10-year-olds and 41.9 for 13- and 14-year-olds. About half of the items for the younger group and 85 percent of the items for the older group showed status differences large enough to be significant at the 1 percent level. But more than a third of the items for the younger group and a tenth of the items for the older group show status differences too small to be significant at the 5 percent level. However, it should be noted that very few items showed negative status differences (i.e., more lower-status pupils got them correct); this occurred on only 5 percent of the items taken by the 9- and 10-year-olds and 0.6 percent of the items taken by the 13- and 14-year-olds. The fact of variation in status differences across items indicates very little by itself, without some external standard against which to compare it, and unfortunately Eells’s study provides no such standard for comparison. A useful standard might be the distribution of index differences between two age groups, say, 9-year-olds and 10-year-olds, all of whom are of the same social status. (One could assure sameness of social background by using siblings reared together.)

2. Ethnic differences do not vary across test items. If cultural differences were to be found in this study, one might expect to find them most in the ethnic group as contrasted with the Old American group. Eells compared only the low-status ethnics with low-status Old Americans. (There were not enough high-status ethnics for statistical comparisons.) These groups differed only about 3 IQ points, on the average. Only 1.9 percent of the items showed index differences between these groups large enough to be significant at the 1 percent level, and more than 91.5 percent of the differences were too small to be significant at the 5 percent level. In short, the item analysis did not reveal any appreciable item index differences between two groups that, although presumably culturally different, did not differ in overall IQ. (Eells tries to explain this finding by saying that his method of identifying ethnic pupils was not entirely satisfactory.) This finding raises the question of the range or variance of item index differences that would be found either for (1) two groups of Old Americans all of the same social status but differing as much in overall IQ as do the high- and low-status groups or (2) high- and low-status Old Americans of the same overall IQ. Although the mean status differences in item difficulty index between any two groups will of course be a direct function of their mean difference in IQ, the variance of the distribution of item index differences could well be more a function of a difference in overall ability than a difference in social status. These comparisons would have yielded a much more telling test of Eells’s hypothesis that social-class differences in IQ are largely due to culturally biased test items than to any of the analyses that Eells provided. The failure to find greater than chance item differences between ethnics and Old Americans, groups that ostensibly differ in cultural background, is actually inconsistent with the culture-bias hypothesis. It is a point seldom mentioned in secondary accounts of Eells’s work.

3. Status differences are greater on the easier test items. Status differences in the index of item difficulty are related to the difficulty level of the items. Contrary to Eells’s expectation, the largest status differences were found on the easier items rather than on the more difficult ones, and this relationship was especially marked in the case of verbal items. This relationship held up throughout the full range of item difficulty, when the measure of item difficulty was based on either the high- or the low-status group. If item difficulty in general depends on relative unfamiliarity or strangeness of the vocabulary or information content of the item, one should expect that the more difficult items (i.e., items with the least familiar content) would show the largest status differences. But in fact just the opposite was found. Eells states:

The hypothesis of cultural bias in the items . . . seems completely inadequate to explain the findings. The easier items may be presumed to be those which involve words and objects which are most likely to be familiar to all status groups, while the more difficult items are probably those which involve words and objects more likely to be familiar to high-status pupils alone. In terms of this hypothesis, therefore, one would expect results exactly the opposite of those found. (p. 65)

4. Status differences vary by type of test item. When items were classified according to type of symbols used and type of question asked, the mean status differences were largest for verbal and smallest for picture, geometric design, and stylized drawing items. Also, the dispersion (i.e., standard deviation) of status differences was greater for verbal and pictorial items than for geometric designs, stylized drawings, number combinations, and letter combinations.

Eells explains the larger status differences shown by verbal items in terms of the academic or bookish vocabulary of many verbal items, which involve words, objects, or concepts with which high-status students have greater opportunity for becoming familiar. Eells notes, however, that there were many items that showed large status differences for which no particular explanation is apparent and through which runs no common feature, except that they were usually verbal. Because these were all group-administered tests, the verbal items necessarily depend on reading skill. Eells did not consider the question of how much the status differences on the verbal items could be attributed simply to the well-established social-status differences in reading skill, particularly reading comprehension, which itself is quite highly correlated with g.

Items showing the smallest status differences were nearly always nonverbal or involved simple everyday words not intended to test vocabulary. The one complete test showing the smallest status differences was the Spatial Visualization Ability Subtest of Thurstone’s Primary Mental Abilities. (Later studies have also shown quite small SES differences on tests of spatial ability relative to IQ differences.) But the Spatial Ability test has the lowest g loading of any of the Primary Mental Abilities, which suggests the hypothesis that status differences are directly related to the item’s g loading. It is a pity that Eells did not factor analyze the items (or scores based on subsets of highly similar items) and examine the relationship between items’ factor loadings and status differences in item difficulty, but that would have been exceedingly costly in time and effort in the days before high-speed electronic computers.

Within either verbal or nonverbal classes of items no one type of item (e.g., analogies, opposites, classification, etc.) consistently showed larger or smaller status differences.

5. Few differences arise in choice of error distractors. The high- and low-status groups were also compared in the frequencies with which they made errors on the different multiple-choice distractors. Of the 315 multiple-choice items, 75 showed significantly different patterns of errors for the two groups. Eells could give a plausible explanation for a number of these error differences in terms of status differences in opportunity for familiarity with the content of the various error distractors. But most of the items did not readily yield to this kind of explanation. The errors of high-status children, more frequently than those of low-status children, consisted of choosing the one distractor that was most nearly correct or logically closest to the correct answer. Low-status children tended to spread their errors more evenly across the several distractors, as one would expect to find if they engaged in more random guessing. (There were no significant status differences in the proportions of all noncorrect responses that consisted of omissions.)

Choice of distractors has since been found to be related to mental age and chronological age in culturally homogeneous groups, in a way much like the status differences described by Eells. That is, when brighter or more mature children make errors on a multiple-choice test, they tend to make “better” or more sophisticated choices from among the several distractors. Moreover, as persons reach the more difficult items, they show a greater tendency to guess at the answers and the guesses become more random with the increasing difficulty of the items. Low-status pupils, for whom more items are in the high range of difficulty, thus have a greater opportunity to engage in “wild guessing.” [...]

The McGurk Study. ... McGurk’s (1951) doctoral study took a closer look at this type of question in terms of the rated “culture loading” of well-known standardized tests of intelligence, such as the Otis Test, Thorndike’s CAVD, and the ACE test. A panel of 78 judges, including professors of psychology and sociology, educators, professional workers in counseling and guidance, and graduate students in these fields, were asked to classify each of 226 test items into one of three categories: I, least cultural; II, neutral; III, most cultural. Each rater was permitted to ascribe his own meaning to the word “cultural” in classifying the items. McGurk wanted to select the test items regarded as the most and the least “cultural” in terms of some implicit consensus as to the meaning of this term among psychologists, sociologists, and educators. Only those items were used on which at least 50 percent of the judges made the same classification or on which the frequency of classification showed significantly greater than chance agreement. The main part of the study then consisted of comparing blacks and whites on the 103 items claimed as the most cultural and the 81 items claimed as the least cultural according to the ratings described. The 184 items were administered to 90 high school seniors. From these data, items classed as “most cultural” were matched for difficulty (i.e., percentage passing) with items classed as “least cultural”; there were 37 pairs of items matched (±2 percent) for difficulty.

These 37 pairs of matched items were then administered as a test to seniors in 14 high schools in Pennsylvania and New Jersey, totaling 2,630 whites and 233 blacks. Because there were so many more whites than blacks, it was possible for McGurk to obtain practically perfect matching of a white pupil with each of 213 black pupils. Each black pupil was paired with a white pupil in (1) the same curriculum, (2) the same school, and (3) enrollment in the same school district since first grade. The white-black pairs were also matched so that the white member of each pair was either equal to or lower than the black member on an eleven-item index of socioeconomic background (the Sims Scale). (Exact matching on the eleven items of the SES index was achieved, on the average, in 66 percent of the 213 matched black-white pairs.) The matched black and white groups averaged 18.2 and 18.1 years of age, respectively.

McGurk’s findings can be summarized in five main points.

1. On the total test for the matched groups, the white-black mean difference, expressed in standard deviation units, is 0.50σ.

2. On the thirty-seven test items classified as “most cultural,” the white-black mean difference is 0.30σ. On the thirty-seven test items classified as “least cultural,” the white-black mean difference is 0.58σ. In other words, the white-black difference on the “least cultural” items is almost twice as great as on the “most cultural” items.

3. To determine if finding 2 was merely a result of differences in item difficulty between the most and least cultural items, McGurk obtained twenty-eight pairs of “most” and “least” cultural items matched (±5 percent) for difficulty (based on the percentage passing the items in the combined white-black samples). On these sets of most and least cultural items matched for difficulty, the white-black mean difference is 0.32σ on the “most cultural” items and 0.56σ on the “least cultural” items. In short, the results in finding 2 cannot be attributed to differences in item difficulty per se between the most and least cultural items. Blacks perform relatively better on the items judged as the more culture loaded when item difficulty is held constant. In 1951 this was considered a most surprising finding.

4. The item difficulties (percentage passing) separately for blacks and whites are correlated with each other .98 for the “most cultural” and .96 for the “least cultural” sets of difficulty-matched items. Thus there is a high degree of similarity in the items’ relative difficulties for whites and blacks or, conversely, a practically negligible race x item interaction for both the most and the least culture-loaded items.

5. McGurk also wished to determine the way in which SES interacted with black-white differences on the sets of items judged as the most and the least cultural. The 25 percent of whites and blacks who ranked the highest and the 25 percent who ranked the lowest on the SES index were selected as the high-SES and low-SES groups for further analysis. There were fifty-three subjects of each race in each SES group. The results are summarized in Table 11.1 in terms of the mean difference expressed in standard deviation units.

The pattern of differences seen in Table 11.1 shows definite interactions among race, SES, and item type that are quite contrary to popular expectation. As one might expect, the most cultural items show a larger difference between high- and low-SES whites than the least cultural items. But just the opposite is true for blacks; the SES differences are greater for the least culture-loaded items. Also, the difference is considerably greater between whites and blacks matched for high SES than between whites and blacks matched for low SES, and this rather surprising result is even exaggerated on the most cultural items. This is quite inconsistent with the hypothesis that the white-black difference in test scores is due to the culture loading of the items, at least as the culture loading of test items is commonly judged.

One possible explanation for McGurk's seemingly paradoxical results is to be found in the fact that blacks perform better on tests involving rote learning and memory than on tests involving relation eduction or reasoning and problem solving, especially with content of an abstract nature. [...]

In the most general terms, blacks perform relatively less well on test items that involve greater cognitive complexity. By cognitive complexity I mean the mental manipulation or transformation of the item input required to produce the correct output. Item complexity, in this sense, is quite distinct from item difficulty, which is defined as the percentage of subjects who can pass the item. It is hypothesized that the more culturally loaded items at a given level of difficulty are not as cognitively complex as the less culturally loaded items at the same level of difficulty.

In general, the difficulty of the most culturally loaded items depends more on past learning and memory, whereas the difficulty of the least culturally loaded items depends more on the complexity of the reasoning needed to produce the correct answer. In other words, the most cultural items might be less g loaded than the least cultural items. [...]

Recent Studies of Verbal versus Nonverbal IQ Difference. ... McGurk (1975) has reviewed virtually the entire published literature between 1951 and 1970 on the question of whether verbal or nonverbal intelligence tests show greater discrimination between the scores of blacks and whites. From 1,720 articles listed in Psychological Abstracts as dealing with “race” or “Negro,” McGurk found 80 articles that contain objective test data comparing blacks and whites and 25 articles that compare blacks and whites on both verbal and nonverbal tests. McGurk determined the median overlap of the black and white distribution of scores on verbal and nonverbal tests. (Median overlap is the percentage of blacks whose test scores exceed the median of the whites’ score distribution.) The average median overlap in all eighty studies is 15 percent (equivalent to an IQ difference of approximately 16 points). The verbal and performance subtests of the Wechsler show greater overlap for the verbal tests (see Table 11.2). The verbal and performance subtests of the Wechsler are well characterize by Sattler (1974):

[T]he Verbal Scale is relatively highly structured, is dependent on the child’s accumulated experience, and usually requires the child to respond automatically with what he already knows, whereas the Performance Scale is relatively less structured, is more dependent on the child’s immediate problem solving ability, and requires the child to meet new situations and to apply past experience and previously acquired skills to a new set of demands, (p. 206)

Contrary to popular expectation, as can be seen in Table 11.2, there is significantly greater black-white median overlap on the verbal than on the nonverbal tests.

McGurk did not consider the Stanford-Binet IQ test, probably because the verbal and nonverbal items are not scored separately as in the Wechsler tests. Kennedy, Van de Riet, and White (1963), however, did an item analysis of the 1960 revision of the Stanford-Binet given to 1,800 randomly sampled black children in five southeastern states. Examining the percentage of the sample passing each item, the authors concluded, “There does not seem to be any exceptionally high performance ability in contrast to low verbal ability for this sample, as suggested by authors” (p. 109). The largest and probably most representative white and black samples ever tested on the same verbal and nonverbal tests are those in the Coleman report (Coleman et al., 1966), which McGurk did not include in his review. The mean white-black difference (expressed in white σ units) on the tests of verbal ability given in grades 1, 3, 6, 9, and 12 is 1.02σ; on nonverbal ability the difference is 1.05σ. The difference of 0.03σ is trivial, for all practical purposes, but it fails to support the notion that blacks do worse on verbal than on nonverbal tests.

An especially valuable set of data for consideration of this question is found in a study by the U.S. Public Health Service (Roberts, 1971). As a part of the National Health Survey, a sample of 7,119 children was selected in such a way as to be representative of the roughly 24 million noninstitutionalized children 6 through 11 years of age in the United States. Approximately 1,000 children were examined in each age group. Approximately 14 percent of the sample were black. All children were given two subtests from the Wechsler Intelligence Scale for Children - Vocabulary and Block Design. This choice of tests is ideal for two reasons: (1) The combined Vocabulary and Block Design tests correlate more highly (+.88) with the WISC Full Scale IQ than does any other combination of two subtests for both blacks and whites and (2) in a factor analysis done on the age 10 group, Vocabulary has the largest g loading (about .80) of any of the verbal subtests and Block Design has the largest g loading of any of the performance subtests. Vocabulary, however, is slightly more g loaded than is Block Design. The mean black-white difference, relative to the average standard deviation within groups, is approximately constant across all ages from 6 through 11 and appears at all economic and educational levels of the children’s parents as shown in Figures 11.1 and 11.2.

The average white-black difference is 0.78σ on Vocabulary and 0.76σ on Block Design. The difference of 0.02σ is significant, but utterly trivial. It suggests that in large representative samples of American blacks there is probably little, if any, difference in level of performance on verbal and nonverbal tests, provided they have comparable g loadings. My perusal of all the available evidence leads me to the hypothesis that it is the item’s g loading, rather than the verbal-nonverbal distinction per se, that is most closely related to the degree of white-black discrimination of the item. This observation was first made by Spearman (1927). In commenting on a study of 10 different mental tests administered to 120 black and 2,000 white American children of ages 10 to 14, Spearman noted that the blacks, on the average, showed poorer performance than whites on all ten tests, “but it was most marked in just those which are known to be most saturated with g” (p. 379). We shall examine this hypothesis more closely in the next section.

Jensen (1974a) compared California elementary school whites (N = 638), blacks (N = 381), and Mexican-Americans (N = 644) on verbal and nonverbal tests that were perfectly matched on difficulty for white males (N = 333). The verbal test was the Peabody Picture Vocabulary (PPVT); the nonverbal test was Raven’s Colored Progressive Matrices. These two tests seem ideal for examining our hypothesis. The PPVT consists of 150 plates each bearing four pictures; the examiner names one of the four pictures and asks the subject to point to the appropriate picture. The plates are presented in the order of the difficulty level of the stimulus words in terms of percentage passing in the normative sample. The level of item difficulty, and hence the rank order of the items’ presentation, is quite closely related to the relative frequency of the occurrence of the stimulus words in the English language. Figure 11.3 shows the mean frequency of the PPVT stimulus words per million words, as tabulated in the Thorndike-Lorge (1944) general word count in American newspapers, magazines, and books. This indicates that the PPVT item difficulty is closely related to the rarity of the words in general usage in American English, and this is mainly what is meant by “culture loaded.”

The contrasting test, in this respect, is the Raven Colored Progressive Matrices, which consists of thirty-six colored multiple-choice matrix items. This nonverbal test was specially designed to reduce item dependence on acquired knowledge and to keep cultural and scholastic content to a minimum while calling for reasoning ability. The difficulty level of the items is dependent on their degree of complexity, involving nonrepresentational figural material and the number of figural elements and abstract rules that must enter into the reasoning process required for correct solution. Examples of the PPVT and Progressive Matrices items are shown in Figure 11.4.

Because there are only 36 colored matrices items and 150 PPVT items, it was possible to obtain perfect matching of item difficulties on each of 35 pairs of matrices and PPVT items in the sample of white males, so that the means and standard deviations on these two subtests were identical in this sample.

We can then ask the crucial question: how large are the mean differences between these two contrasting tests, the PPVT and matrices, which were perfectly matched for difficulty on white males, when given to samples of blacks, Mexican-Americans, and white females of the same age?

It turns out that there is no significant mean difference between the matrices and PPVT scores within the groups of white females, black males, and black females. (In fact, white females show a larger difference than black males.) Both male and female Mexican-American children, on the other hand, score significantly (p < .01) lower on the PPVT than on the matrices. Many of the Mexican-American children were from Spanish-speaking and bilingual homes, which may account for their obtaining significantly lower scores on the PPVT as compared with the matrices.

Thus, matrices and PPVT items intentionally matched on difficulty for white males are also thereby matched on difficulty for black males and females. The correlation between the p values (percentage passing) of the matched pairs of matrices and PPVT items is .94 for white females, .97 for black males, and .93 for black females. It appears from these findings that blacks perform no less well on a culturally loaded verbal test, the PPVT, than on a culture-reduced nonverbal test, the Colored Progressive Matrices, when these tests are perfectly equated in difficulty for whites.

All the findings reviewed here would seem to contradict the common belief that the majority of black children have a language different from standard American English, which supposedly handicaps them in taking IQ tests and in scholastic achievement. The fact that blacks perform at the same level on both verbal and nonverbal tests suggests that their overall lower test scores, relative to whites, is not attributable to a language deficit per se. By contrast, immigrant children, with little or no knowledge of English, score markedly higher on nonverbal than on standard verbal tests in English. Also, children who are bom deaf and are therefore severely language deprived perform much less well on verbal than on nonverbal tests (Vernon, 1968). Moreover, a comprehensive review of the research pertaining to the “different language” hypothesis of the black IQ deficit found no evidence to support it. The authors concluded: “In general, no acceptable, replicated research has found that the dialect spoken by black children presents them with unique problems in comprehending standard English” (Hall & Turner, 1974, p. 79). [...]

Wechsler Intelligence Scale for Children. A doctoral study by Nichols (1972) provides relevant data on seven subtests of the WISC, in addition to six other ability and achievement tests, given to large samples of white (N = 1,940) and black (N = 1,460) 7-year-olds in several large cities. ... The subjects were enlisted in twelve public hospitals at the time of their mothers’ pregnancy and are a fairly representative sample of the populations served by these large city hospitals, a population that Nichols describes as “skewed somewhat to the lower end” in social class.

Nichols notes (p. 83) that the intercorrelations among the thirteen tests are highly similar in the white and black samples, as indicated by a correlation of .954 between the two correlation matrices. Obviously the factor structure of these variables is bound to be highly similar for whites and blacks, and factor analysis bears this out. The g factor loadings extracted from these correlation matrices are shown in Table 11.3 along with the mean white-black difference expressed in σ units. The chi squared test of the overall significance of the white-black difference in g loadings of the thirteen tests yields a χ² = 1.31, which is nonsignificant even with these very large samples. The correlation between the white and black g loadings is .98, which for 12df (degrees of freedom) is significant beyond the .001 level of confidence.

Regarding the Spearman hypothesis referred to in the preceding section, the correlation between the mean white-black differences and the g loadings on the thirteen tests is .69 (p < .01) for whites and .71 (p < .01) for blacks. If we compare (1) the mean white-black difference (in σ units) on the six tests with the highest g loadings with (2) the mean white-black difference on the seven tests with the lowest g loadings, we have .70σ - .46σ = .24σ, which is a highly significant difference (noncorrelated t = 6.92, df = 3398, p < .001). Thus Spearman’s hypothesis would seem to be borne out by these data. Certainly it is not contradicted. Yet there is a question, as the g loadings on some of these tests are not in marked agreement with their g loadings where they have been factor analyzed in other contexts. We are safest in concluding only that the white-black differences are quite highly correlated with the tests’ g loadings in this particular battery, for both whites and blacks. Another way of describing these results is to say that those tests that best discriminate individual differences among whites are the same tests that best discriminate individual differences among blacks and are also the same tests that discriminate the most between whites and blacks.

The racial aspect of this finding, however, is ambiguous, being confounded with socioeconomic status. (This fact should not be interpreted to mean that SES is necessarily a cause of the observed mean white-black difference in test scores.) Nichols provides SES ratings and their correlations with each of the thirteen tests. The average correlation is only .25 for whites and .20 for blacks. But the more important points are that (1) SES correlates with the g factor .51 in the white sample and .42 in the black and (2) the correlations rxy between x = the correlation of SES with scores on a given test and y = the mean white-black difference (in σ units) on the given test over the thirteen tests is .72 for whites and .79 for blacks. In other words, the tests’ correlations with SES are related to he mean white-black test differences to a slightly greater degree than the tests’ g loadings are related to the white-black difference. And within each racial group SES is more highly correlated with g than with any particular test. But this aside should not obscure the fact that there is nothing in this study that suggests that any of the thirteen tests in this battery is biased with respect to whites and blacks. The battery is factorially almost identical in the two races. [...]

Fluid and Crystalized g. Travis Osborne has provided data on twelve quite diverse tests given to white (N = 608) and black (N = 246) urban school children in Georgia. Eight of the tests are from the Educational Testing Service “Kit of Reference Tests for Cognitive Factors” (French et al., 1963). The tests fall into two categories similar to what Cattell (1971b) has characterized as “fluid” and “crystalized” intelligence, or gf and gc. The two categories of tests are as follows:

“Fluid”                                           “Crystalized”

Cube Comparisons                      Calendar Test
Identical Pictures                        Arithmetic
Formboard                                   Vocabulary (Wide Range)
Surface Development                 Vocabulary (Heim)
Spatial                                           Spelling
Paper                                             Folding
Object                                           Aperture

The “fluid” tests are all nonverbal and nonscholastic and do not call on any specific knowledge acquired outside the testing situation.

I have factor analyzed this battery of twelve tests separately in the white and black samples. Chronological age (in months) was partialled out of all the intercorrelations. The rotated factors clearly divide up into gf and gc, which together account for 48.6 percent of the total variance in whites and 48.5 percent in blacks. The gf accounts for 24.7 percent and 25.1 percent for whites and blacks, respectively; the corresponding figures for gc are 23.9 percent and 23.4 percent. The loadings on gf are correlated .81 (p < .01) between whites and blacks, and the loadings on gc are correlated .93 (p < .01). Even with this high degree of similarity between the racial groups on gf and gc, the chi squared test shows the overall differences in factor loadings between the groups to be significantly different: for gf, χ² = 7.76, p < .01; and gc, χ² = 4.36, p < .05. But of course quite small differences in factor loadings can be statistically significant with such a large sample (N = 854).

The Spearman hypothesis was tested on these data for both gf and gc. The correlation between (1) the tests’ loading on gc and (2) the mean white-black difference on the tests is -.24 for the white gc loadings and -.02 for the black; both r’s are nonsignificant. The correlation between loadings on gf and the mean white-black difference is +.56 (p < .05) for whites and +.42 (p < .10) for blacks. Thus, the mean white-black differences on the twelve tests are more highly related to the tests’ loadings on gf than on gc. This finding contradicts the common notion that the white-black difference on tests largely involves differences in past learning as characterized by the “crystalized” component of variance in test scores. Instead, we find that the white-black differences on various tests are more closely related to the “fluid” component of test score variance. [...]

Socioeconomic Status. ... Large samples of suburban (N = 3,994) and “inner-city” (N = 1,501) school children in Milwaukee took the Lorge-Thorndike Verbal and Nonverbal IQ scales and the Iowa Tests of Basic Skills, a scholastic achievement battery consisting of eleven subtests covering most of the traditional academic subject matter of the elementary school (Crano, 1974). The very same samples were tested in both grades 4 and 6, and the intercorrelations among all the tests, as well as the total IQ and composite achievement score, in both grade levels, totaling thirty variables in all, were used for the following analyses. The suburban children were mostly of middle and upper-middle SES and will henceforth be labeled Upper-SES. The inner-city children were in schools that qualified for aid under Title 1 of the Elementary and Secondary Education Act, intended to improve the education of the disadvantaged. This group is labeled Lower-SES. Although no information is given on the racial composition of these groups, the inner-city schools of Milwaukee are racially mixed, with a predominant percentage of blacks.

The general factor extracted from the intercorrelations among the thirty IQ and scholastic achievement variables accounts for 59.5 percent of the total variance in the Upper-SES and 51.4 percent in the Lower-SES group, a highly significant (p < .001) difference with these large samples. The tests with the largest g loadings in this battery, in both samples, are Composite Achievement and Verbal IQ. The correlation between the g loadings of the Upper- and Lower-SES groups is .83 (p < .001), indicating a high degree of similarity in the pattern of g loadings, although the overall difference between the g loadings of the Upper- and Lower-SES groups is highly significant (χ² = 28.8, p < .001), since the Upper-SES sample has rather uniformly larger g loadings on nearly all the tests. A significant difference in the overall size of factor loadings, when the pattern of loadings is highly similar, suggests either (1) restriction of range in the Lower-SES sample, or (2) differential reliability in different ranges of the scale of scores on the various tests, or both.

This point is clearly illustrated in an important study by Humphreys and Taber (1973). From the massive data bank of Project TALENT, they selected for comparison four groups of ninth-grade boys, without regard to ethnic background, as follows:

A factor analysis was performed separately on each of the four samples on a battery of twenty-one diverse ability and scholastic achievement tests. In all groups, varimax rotation of the principal factors yielded six interpretable factors labeled Academic Achievement, Verbal Comprehension, Spatial Visualization, Clerical Speed, Rote Memorization, and Verbal Fluency. Concerning the rotated factors, Humphreys and Taber conclude:

There were no important differences between either factors or factor loadings associated with differences in socioeconomic status. The same factors were also defined by groups high and low in intelligence, but there were fairly numerous large differences in sizes of loadings associated with the intelligence variable. When analyzed further most of these differences in loadings were explained by the characteristics of the scales of measurement. Some scales were too easy for the high intelligence groups and some too difficult for the low intelligence groups, thus producing differential reliability in different parts of the several scales. In a small number of variables, however, there is evidence for differences in factor loadings as a function of the intellectual level of the subjects that cannot be explained by the characteristics of the scales. (1973, p. 114)

Table 11.7 shows the correlation between the various IQ x SES groups’ factor loadings on the twenty-one tests for all six factors. Note that when IQ is constant and SES varies, the correlations are higher than when SES is constant and IQ varies. The average correlation over all factors for same IQ/different SES is .97, for same SES/different IQ is .84, and for different SES/different IQ is .85. This means that the groups’ differences in the tests’ factor loadings are more related to the groups’ differences in level of performance than to their differences in SES. The fact that some of the tests fail to measure certain factors equally well at all levels of IQ is, of course, no less a psychometric defect than if they failed to do so across different levels of SES.

Similarity of Factor Structure between and within Families. ... Any test score differences among children in the same family cannot be regarded as being due to differences in cultural background, whereas such differences between children from different families may or may not reflect cultural differences. [...]

The percentage of the total variance accounted for by the first principal component or g factor in each of the four matrices is

–                                            White       Black
Between families                66.6%     61.0%
Within families                   51.9         52.4

The between-families g accounts for a larger percentage of the total variance because the scores entering into the correlations are more reliable, being the means of two or more siblings on a given test. (The means of any two or more correlated measurements are always more reliable than the single measurements.) By the same token, the within-family correlations, based on the differences between siblings on a given test, are necessarily less reliable. (Differences between any two imperfectly reliable measurements are always less reliable than either of the single measurements.)

The pattern of g loadings on the seven tests is highly similar across the four groups, as shown by the cross-group correlations between the tests’ g loadings:

–                                                          W b-f   W w-f   B b-f   B w-f
White between-families   W b-f                    .95       .84      .97
White within-families      W w-f                                .95      .94
Black between-families     B b-f                                            .88
Black within-families        B w-f                                              –

These correlations are statistically homogeneous; that is, they do not differ significantly from one another. Thus it appears that the g loadings of these seven tests show a very similar pattern regardless of whether they were extracted from the within-family correlations (which completely exclude cultural and socioeconomic effects in the factor analyzed variance) or from the between-families correlations, for either whites or blacks. ... This outcome would seem unlikely if the largest source of variance in these tests, reflected by their g loadings, were strongly influenced by whatever cultural differences that might exist between families and between whites and blacks.

We can also test the Spearman hypothesis on these data. Because the pattern of g loadings on the seven tests is so highly similar in both racial groups and for both the between- and within-family conditions, I have averaged the four sets of g loadings (via Fisher’s z transformation) on each test and correlated these seven averages with the mean white-black differences (in σ units) on the seven tests. The correlation is +.78 (p < .05). Also, the mean white-black difference on the three most g-loaded tests is significantly (p<.001) greater than on the three least g-loaded tests, consistent with Spearman’s hypothesis.

A Closer Look at the Spearman Hypothesis. There is an obvious ambiguity in the interpretation of all the evidence presented relevant to Spearman’s hypothesis, which states that the magnitude of the white-black difference on various tests is directly related to the tests’ g loadings. The reason for the ambiguity is, of course, that a given test’s g loading is not invariant when the test is factor analyzed among different collections of other tests. A test’s g loading, in fact, can vary considerably depending on the composition of the battery of tests among which it is factor analyzed. The g factor itself is not invariant from one test battery to another, although the interbattery correlation on g is usually quite substantial when both batteries, even though they have no tests in common, consist of a dozen or more diverse tests of cognitive ability. [...]

The alternative interpretation is that whites and blacks differ merely in overall level of performance on all test items (i.e., there is no race x items interaction), and those items (or subtests) that contribute the most to the true-score variance (by virtue of high reliability and optimal difficulty level) among individuals of either race thereby also show the largest mean differences between the races, and they are also the most heavily loaded on a general factor (i.e., the first principal component) that, by its mathematical nature, necessarily accounts for more of the variance than any other factor, regardless of the psychological nature of the first principal component extracted from the particular collection of tests. By this interpretation, the only condition needed to yield results at least superficially consistent with Spearman’s hypothesis is that there be no appreciable race x items or race x tests interactions or, in other words, that the tests not be racially biased. A corollary of this alternative interpretation of the results we have examined is that the mean difference between the races has essentially the same factor composition as individual differences within each of the races. [...]

One such distinction that has held up in many studies is the contrast between tests of rote learning and short-term memory, on the one hand, and tests of reasoning and problem solving, on the other. The rote learning and short-term memory abilities are measured by tests such as digit memory span, serial and paired-associate learning, and immediate free recall of a set of familiar objects or common nouns. Reasoning, problem solving, and the use of concepts, which exemplify Spearman’s definition of g, are measured by most tests of general intelligence and especially by verbal and figural analogies, number series, and progressive matrices. I have elsewhere (Jensen, 1968b) labeled these two classes of abilities level I and level II. Level I involves the registration and consolidation of stimulus inputs and the formation of simple associations. There is little transformation of the input and thus a high degree of correspondence between the form of the stimulus input and the form of the response output. Level II ability, on the other hand, involves self-initiated elaboration and transformation of the stimulus input before it eventuates in an overt response. The person must consciously manipulate the input to arrive at the correct output. Thus the crucial distinction between levels I and II involves a difference in the complexity of the transformations and mental manipulations required between the presentation of a given mental task to the person and his or her end response to it. Various cognitive tasks ranging along the level I-level II continuum would also correspond closely to their arrangement along the continuum of g loadings in the Spearman sense.

Numerous studies of the past decade have clearly demonstrated an interaction between race (white-black) and level I versus level II tests (Jensen, 1970b, 1970c, 1971a, 1973d, 1974b). Whites and blacks differ much less on the level I than on the level II abilities. Also, in factor analyses the level I tests have much smaller loadings on the g factor or first principal component than do the level II tests. These findings lend support to Spearman’s hypothesis. A rather striking demonstration of this phenomenon consisted of comparing large groups of white and black children, 5 to 12 years of age, on forward and backward digit span (FDS and BDS). FDS and BDS are highly similar tasks, but BDS obviously requires more mental manipulation and transformation of the input. In FDS the examiner reads a series of digits at the rate of one digit per second, and the subject is required to repeat the string of digits in exactly the order in which they were presented. In BDS the subject is required to recall the digits in reverse order, which calls for mental transformation of the input order of the digits. Interestingly, it was found that BDS is significantly more highly correlated with the WISC-R Full Scale IQ than is FDS, in both the white and the black samples. (The Digit Span tests, of course, were not included in the WISC-R IQs.) This finding, along with the fact that the WISC-R Full Scale IQ is a good measure of Spearman’s g, means that BDS is significantly more g loaded than is FDS. Also, the white-black mean difference (in σ units) was more than twice as great on BDS as on FDS. This marked interaction persists even when SES is controlled, as shown in Figure 11.5. ... Subsidiary studies indicated that these results could not be explained in terms of differences in task difficulty per se between FDS and BDS, race differences in test anxiety, or the race of the examiner (Jensen & Figueroa, 1975). Further evidence that the white-black difference is related more to task complexity (and hence Spearman’s g) than to difficulty per se (as indexed by percentage passing) is shown in several studies of visual reaction time (RT), in which whites and blacks were found to differ much less on simple RT than on choice RT, with the white-black difference in mean RT increasing as a function of the number of response alternatives in the choice RT (see Chapter 14, pp. 704-706). The results are highly consistent with Spearman’s hypothesis, if we interpret g as information processing capacity, in which individual differences can be revealed by varying the complexity of the stimuli that must be processed prior to the subject’s final overt response.

The relevance of level I-level II abilities to the interaction of race with the form of the test items has been shown in two studies by Longstreth (1978). From the nature of the level I-level II distinction, Longstreth predicted that multiple-choice and essay types of tests should load higher than true-false tests on level II ability. This prediction is consistent with the interpretation of level II or g as information processing capacity. For example, the multiple-choice format, with its several available response alternatives, is informationally more loaded and complex, calling for more discriminative decisions, than the two-choice true-false format. Essay questions call for considerable internal processing, selection, reconstruction, mental manipulation, and transformation of information stored in memory, which are all level II functions.

Longstreth’s prediction was borne out significantly and replicated in a second study in groups of white, black, Asian-American, and Mexican-American college students, who were given true-false, multiple-choice, and essay tests covering the content of a course in developmental psychology. In addition, the students were given a level I test (Forward Digit Span) and a level II test - the Cognitive Abilities Test (CAT), Nonverbal Battery (a successor to the Lorge-Thorndike Intelligence Test), which is highly loaded on Spearman’s g). The multiple-choice and essay tests are correlated significantly higher with each other than either one correlates with the true-false test, and the pattern of correlations indicates the multiple-choice and essay tests are more loaded on level II than on level I, whereas the true-false test comes close to level I.

If true-false items are less complex and therefore somewhat less g loaded than either multiple-choice or essay questions, we should expect an interaction between item types and race, if Spearman’s hypothesis is valid, with a smaller white-black difference (expressed in σ units) on the true-false test than on the multiple-choice and essay tests. This is exactly what Longstreth found, as shown in the left panel of Figure 11.6. The right panel compares the four racial groups on the multiple-choice test alongside tests that are relatively pure level II and pure level I - the Cognitive Abilities Test and Forward Digit Span, respectively. These results are not only highly consistent with the Spearman hypothesis, but they also indicate an important point for the analysis of test items x group interactions in the study of test bias, namely, that some of the interaction may be due to the strictly formal characteristics of the test items, which should not be confused with cultural bias.

Item x Group Interaction

An item x group interaction exists when all the items in the test do not maintain the same relative difficulties in both the major and minor groups. The interaction of items and groups can be approached either through the analysis of variance of the items x groups x subjects matrix or through the correlation of item difficulty indices across groups. Both methods yield essentially equivalent results when applied to the same set of data. But each method highlights different features of the data, which aids in the detection of test bias. One or both of these methods have been applied to several widely used tests.

Wechsler Intelligence Scale for Children. The WISC is probably the most frequently used individual test of intelligence for school-age children. It has been a popular target for accusations of culture bias, particularly with respect to black children, and therefore warrants thorough analysis.

The present analyses are based on longitudinal WISC data from white and black children in Georgia. [1] The subjects were selected from three Georgia counties representative of small rural, medium, and large industrial populations. The 163 white and 111 black children were given the WISC at ages 6, 7, 9, and 11 years, at about the same time of each year. The whites averaged 1 month older than the blacks. There was some attrition of the sample over the 5 years, so that at age 11 there were only 128 whites and 97 blacks. The white and black IQs differ, on the average, slightly more than one standard deviation (σ = 15 IQ points), as shown in Table 11.8. The overall mean difference in Full Scale IQ is 18.6 points, which is quite typical of the average difference between whites and blacks in the southeastern United States (e.g., Kennedy, Van de Riet, & White, 1963).

Miele (1979) has analyzed these data with respect to test bias and summarizes the results as follows:

The equivalence of the general factor in the two [racial] groups, the overwhelming correspondence in the rank order of item difficulty ... the degree to which the race differences at any given grade level can be simulated by comparing the given group of White children with their performance in the previous grade or the given group of Black children with their performance in the subsequent grade force one to reject the hypothesis that the WISC is a culturally biased instrument for the groups examined.

Let us look at the evidence for the main points in Miele’s summary.

1. Rank Order of Item Difficulty. All the items in nine of the WISC subtests were ranked for percentage passing, separately for boys and girls within each race, at each age level. (The Digit Span and Coding Tests were omitted, as they do not yield dichotomous item scores.) A total of 161 items were rank ordered within each race x sex group at each of four ages. The mean cross-racial rank order correlation for p values (within grades) is .96. For comparison, the rank correlation between the p values of boys and girls of the same race is .98 for whites and .97 for blacks.

I transformed all of the p values to delta (Δ) values, which is an interval scale index of item difficulty, and then obtained the cross-racial Pearson correlations between the Δ values at each age level. Also I determined the average white-black difference in item difficulty, expressed in white σ units. These results are shown in Table 11.9. Fewer items enter into these Δ correlations, since Δ values cannot be computed when p is 1 or 0 in either group. The correlations in Table 11.9 thus are based on only those items that have some variance within both racial groups. It can be seen that the cross-racial correlation of item difficulties is still quite high, averaging .94.

2. Cultural Difference versus Mental Maturity Difference. Miele obtained each item’s correlation (Yule’s Q) with (1) chronological age and (2) race. These correlations thus index the degree to which items (1) discriminate between the same children (of the same race) at different ages and (2) the degree to which the items discriminate between whites and blacks of the same age. Miele found substantial correlations between these two indices, 1 and 2. That is, the items that discriminate most between whites and blacks at any given age are precisely those items that discriminate most between whites at a given age and the same whites at the next earlier age, or between blacks at a given age and the same blacks at the next higher age. Thus the observed white-black differences in item difficulty across the various WISC items can be simulated by comparing older and younger whites or younger and older blacks. (Note that the older and younger groups are the same children tested at different ages.) If the cross-racial variations in differences in item difficulties were due to cultural biases, it would seem a strange coincidence that they should be correlated with age differences within each racial group. Miele suggests that the more parsimonious interpretation of this finding, therefore, is that the pattern of white-black differences in item difficulty reflects differences in level of mental maturity (as measured by the WISC) rather than cultural differences per se. [...]

Out of the 161 items of the WISC compared cross-racially at each of the four age levels, only 12 different items showed a reversal in difficulty, that is, blacks did better than whites on these 12 items. But in no case is the difference in percentage passing statistically significant. Most of these reversals occurred at one or the other extreme of the scale of difficulty, where the measure of item difficulty becomes more unreliable. This evidence is summarized in Table 11.10. It seems highly probable that, if we had very large racial samples, thereby minimizing sampling errors, there would be no item x race reversals whatever.

Let us look at the one item of the WISC that has been held up most often by critics of tests as an especially flagrant example of a culture-biased item for black children. It is the Comprehension subtest item no. 4: “What is the thing to do if a fellow (girl) much smaller than yourself starts to fight with you?” It has been argued that the majority of black children are typically taught to “fight back,” and therefore the keyed correct response to this item runs counter to their cultural values. Yet, out of the 161 items of the WISC this is the forty-second easiest item for blacks (in all grades combined), but it is the forty-seventh easiest item for whites, which indicates that this item is relatively easier for blacks than for whites! As Miele (1979) notes, removing this item from the WISC would, in fact, penalize the black subjects. This nicely illustrates the fallibility of subjective analyses of bias by mere inspection of items. Only proper statistical item analysis methods can reliably establish bias.

Age-lagged Cross-racial Correlations of Item Difficulties on WISC Subtests. Do the lower correlations, that is, those below, say, .95, reflect cultural differences between the two racial groups? Or are they merely a result of the group differences in mental age, as reflected by the mean race difference in Full Scale IQ? To find out, I have computed the ri between whites and blacks of different age levels, comparing younger whites with older blacks. Whites at ages 6, 7, and 9 are compared with blacks at ages 7, 9, and 11. These age-lagged comparisons practically wipe out the mean racial difference in total scores on each of the subtests; that is, the age-lagged blacks have nearly the same mean score as whites of the next younger age.

Under this age-lagged condition, the cross-racial correlations between item difficulties are, in nearly all instances, appreciably higher than the same-age cross-racial correlations. The age-lagged cross-racial correlations, shown in Table 11.12, average .98, which is raised to .99 by correction for attenuation. The fact that the age-lagged cross-racial correlations are very high suggests that the somewhat lower correlations between the same age groups may be due to the white-black differences in mental age rather than to differential cultural biases in the various items.

The only test that still shows unimpressive age-lagged cross-racial correlations is the four-item Object Assembly test. Thus a closer look at the Object Assembly subtest data is called for. The percentage passing each item in each of the age-lagged groups is shown in Table 11.13. The correlations are generally substantial, but we cannot make much of their falling below unity, because with only four items even much lower cross-racial correlations in item difficulty would not be significantly different from unity. (With N = 4, the r would have to be below +.22 to be significantly different from .995 at the .05 level.) Also note that the cross-racial age groups W9B11, unlike the other age-lagged comparisons, are not closely matched for overall difficulty level on the Object Assembly items. Thus the question of bias in the Object Assembly subtest remains in doubt and will have to await cross-validation in other white and black samples, using the methods demonstrated here.

Simulated Cross-racial Correlations by Pseudorace Groups. The age-lagged cross-racial correlations are higher than the corresponding same-age cross-racial correlations, suggesting a mental maturity difference rather than a cultural difference between the same-age race groups. Therefore we should be able to simulate the same kind of mental maturity differences by comparing the very same children (of either race) at younger and older age levels. That is, we correlate the item difficulties of whites at age 6 with the item difficulties of the same whites at age 7, and correlate age 7 with age 9, and age 9 with age 11. We do the same for blacks. When the ratio of the mental ages of the same-persons age-lagged group is approximately equal to the ratio of the mental ages of two same-age racial groups, we call the same-persons age-lagged groups “pseudorace” groups, as they mimic the actual mental-age difference between the actual racial groups when they are matched on chronological age. For example, using W and B to stand for white and black and subscripts to stand for age, the psuedorace comparisons W7W6 should simulate the true cross-racial comparison W7B7; and the pseudorace comparison B7B6 should simulate W6B6, and so forth.

The intraclass correlations between the item difficulties of these pseudorace groups are shown in Table 11.12. It can be seen that their overall average (.93 and .94) is closer to the actual same-age cross-racial correlation (.91) than to the age-lagged cross-racial correlation (.98).

As an index of the goodness of the pseudorace simulation of the cross-racial correlation on the various subtests, I have computed the Spearman rank order correlation between the nine true cross-racial correlations and their pseudorace simulated counterparts. These correlations are shown in Table 11.14. Also shown in Table 11.14 are the ratios of the mental ages for the actual race and the pseudorace comparisons, as explained in the table’s footnote 1. It can be seen that there is a fair approximation of the black-white MA ratios by the pseudorace younger-older MA ratios.

The simulation of the item difficulty cross-racial correlation is quite good; four of the six rank order correlations are quite high and significant beyond the .01 level.

The fact that the cross-racial correlations can be improved by age lagging the racial groups, and that they can also be quite well simulated by creating pseudorace groups of the very same children at different ages within each racial group, is strongly consistent with the hypothesis that the imperfect cross-racial correlations between the item difficulties are due to a racial difference in mental maturity at any given age rather than to differential effects of culture bias in various items within each of the WISC subtests.

The Group Difference / Interaction Ratio. If the magnitude of the cross-group correlation between item difficulty indices is taken as an indicator of item biases when the correlation is significantly less than unity (or the group X item interaction is significant), we should also have an index showing the magnitude of the group mean difference on the test in relation to the magnitude of the group X items interaction. What we wish to determine is (a) how large is the group (e.g., race) difference relative to individual differences within groups, (b) how large is the group x item interaction relative to the individual X item interaction, and, most important, (c) how large is a relative to b? I once termed this final index the a/b ratio (Jensen, 1974a, p. 217); I now think it preferable to call it the group difference-interaction ratio (or GD/I ratio, for short). The less the item biases in a test, the larger should be the GD/I ratio. That is, large values of the GD/I ratio indicate that the group difference is large relative to the group X item interaction. Because test scores and item data are not an absolute scale, the mean group difference and group X item interaction must each be expressed in terms of the individual variation within groups.

Referring to the analysis of variance (see Table 11.11), the GD/I ratio for race may be expressed in three ways that are all exactly equivalent, in terms of the sum of squares (SS), the mean squares (MS), or the F ratios.

where FR is the F ratio for the race main effect and F1 x r is the F ratio for the item X race interaction.

In the example of the ANOVA of the WISC Vocabulary subtest (Table 11.11), the GD/I ratio for race is 3.63.

The GD/I ratio need not be computed unless the item x group interaction is statistically significant. If it is not significant, there is no question of any bias according to this particular criterion. If the item x group interaction is significant, the GD/I ratio indicates how much larger the group main effect is than the group X item interaction. As GD/I approaches zero, the group mean difference becomes increasingly trivial and uninterpretable in terms of any unitary dimension measured by the test. That is, when GD/I is close to unity (or less than 1), we cannot discount the supposition that any significant difference between the groups is due to item biases. It is interesting that the only significant sex difference with a substantial GD/I ratio (4.91) in all these data is for Block Design at age 6. The overall average of GD/I for sex on every subtest at every age level (leaving out only Block Design at age 6) is 0.79, σ = 0.79. The mean sex differences are all very small and usually nonsignificant, and those that are significant are meaningless because of the low GD/I ratio. That is, the item X sex interaction is so large relative to the sex main effect as to render the latter meaningless. It can be the result of item biases.

The GD/I ratios for race, by contrast, are quite large, averaging 5.47, as shown in Table 11.15. Values of GD/I greater than 2 clearly indicate that the mean difference between the groups cannot be attributed to an unfavorable balance of group X item biases and cannot be appreciably reduced by eliminating some items or adding new items selected at random from the same general population of items. When GD/I is close to 1, the possibility exists of reducing the group main effect to nonsignificance by eliminating or adding items of the same type, thereby balancing out the group X item biases and equalizing the group means. In fact, this is precisely what has been done in the construction of some tests in which a sex difference has been purposely eliminated by balancing item biases. This would not be possible if GD/I were not already close to unity and would be practically impossible if GD/I were originally greater than 2.

Notice in Table 11.15 that the age-lagged cross-race comparisons show very small values of GD/I, averaging 0.99. In other words, the black children’s test results at a given age are very much like those of white children who are younger but have approximately the same mental age as the blacks.

Also, we can simulate the same-age cross-race GD/I ratios by means of the pseudorace groups, as shown in Table 11.15. The goodness of this age simulation of the race GD/I ratios for the various WISC subtests is indicated by the rank order correlation between the actual and the simulated ratios, as shown in Table 11.16. Again, it clearly appears that the test differences between whites and blacks of the same age closely resemble the same features as are found in comparing older and younger children of the same race. The race differences thus look more like differences in overall mental maturity rather than like cultural factors interacting with test items. If one were to claim culture bias from these data, one would also have to argue that the cultural biases closely simulate differences in mental maturity among white children or among black children. But this would seem to be a quite farfetched ad hoc hypothesis, especially in view of the great variety of items comprising the WISC.

Stanford-Binet Intelligence Scale. ... Paul Nichols (1972) provides an especially valuable set of data. His samples consist of 2,526 white and 2,514 black children in 12 cities, all tested on the S-B at 4 years of age. The mean S-B IQ difference of 15 points between these samples is close to the difference typically found in most studies of American blacks (Jensen 1973b, pp. 62-66; Shuey, 1966). Because all the children were of preschool age, one should expect any cultural differences that might exist between the whites and blacks to be undiluted by the common environment provided by formal schooling. Another advantage in these data is that the S-B items for 4-year-olds (i.e., S-B items in the III- to V-year range) are an especially diverse collection of items; they are probably more heterogeneous in form and content than the items in any other age range of the S-B or than any set of the same number of consecutive items in any other standard test. Nichols (1972) presents the percentage of whites and blacks passing sixteen consecutive S-B items from age III-6 through V, shown in Table 11.17.

The rank order correlation between the white and black percentage passing (p values) is .99. When the p values are transformed to delta values, thereby representing item difficulties on an interval scale, the cross-racial correlation is .98. The scatter diagram of the delta values is shown in Figure 11.7. It can be seen that the regression is linear and that .98² or 96 percent of the variance in the black delta values can be predicted from the white delta values by the regression equation black Δ = 3.33 + 0.93 white Δ. The overall mean black-white difference in item difficulty is 2.43Δ, or 0.61 σ units. The broken lines fall ±1.96 standard errors of estimate (SEE) from the regression line, which is the 95 percent confidence interval. An item falling outside that range may be considered biased; that is, its difficulty in the minor group cannot be predicted from the item’s difficulty in the major group within the 95 percent confidence interval. By eliminating such items and replacing them with less biased items of comparable difficulty in either the major or minor group, the cross-group item difficulty correlation is increased and the 95 percent confidence interval becomes narrower. A more stringent criterion could be to use the 90 percent confidence interval (i.e., ±1.64SEE). The choice of confidence interval is a policy decision and will be governed by such factors as the resources available for improving the test.

The remarkable feature of the present S-B data is the high cross-racial correlation of the item difficulties. For comparison, we can split the white sample into two half-samples and obtain the item difficulty correlation within the white sample; and we do the same in the black sample. The respective rank order correlations in the white and black split-half samples (boosted by the Spearman-Brown formula for the correlation in the full-size sample) are both .99, which can be compared with the rank order correlation of .99 between whites and blacks. From this evidence it would be hard to argue that there are any appreciable black-white item biases in the S-B in the range of items appropriate for testing most 4-year-olds.

Nichols (1972, Table 16) also reports the point-biserial correlations between each of the sixteen S-B items and total IQ; the average rpbi is .40 for whites and .42 for blacks. The Pearson correlation between the sixteen white and black rpbi's is .85, indicating a high degree of cross-racial similarity in the extent to which the items correlate with total IQ. Nichols also gives the point-biserial correlation of each of the sixteen items with an index of socioeconomic status; these average .13 for whites and .10 for blacks, and the cross-racial correlation between these sixteen pairs of correlations is .81, showing considerable white-black similarity in the extent to which the individual items correlate with SES within each racial group. I have computed the correlation (phi/phi max) of each test item (scored pass = 1, fail = 0) with race (quantitized as white = 1, black = 0). These correlations range from .20 to .60 with an average of .35, σ = .12, over the sixteen items.

The items x race correlations are significantly correlated with the items x total IQ correlation (.74 for whites and .57 for blacks), indicating that the items that correlate the most with individual differences in total IQ within either race also correlate the most with the variable of race. The Pearson correlation between (1) item point-biserial correlations with race and (2) item point-biserial correlations with SES within each race is .69 for whites and .84 for blacks and indicates that race differences and SES differences (within races), whatever their causes, are hardly distinguishable among these sixteen S-B items.

Other evidence I have found as a basis for examining possible item biases in the S-B involves the Vocabulary test. The words in the S-B Vocabulary test are arranged in the order of their p values in the 1937 standardization based on an all-white sample. Kennedy, Van de Riet, and White (1963) obtained the S-B on 1,800 black school children in grades 1 through 6 in five southeastern states, with an overall average S-B IQ of 80.7, σ = 12.4. The sample was of predominantly low socioeconomic status. Kennedy et al. (p. 101) give the percentages of this large sample passing each of the first twenty-six words of the S-B Vocabulary test. The rank order correlation between the words’ difficulty levels in the white standardization sample and in the black sample is .98, which is about as close agreement as one might expect to find even with a white sample tested more than twenty-five years after the standardization sample on which the order of difficulty of vocabulary words was determined. This high degree of cross-racial agreement seems quite remarkable, considering that one might reasonably expect Vocabulary to be perhaps the most prone to cultural bias.

Kennedy et al. (1963) also indicate the percentage of the black sample, separately for each of grades 1 through 6, passing each S-B item. Figure 11.8, which is based on these data, shows the average percentage passing the various S-B items as a function of the item’s mental-age placement as determined in the 1937 standardization on a white population sample. It can be seen that at each grade level the percentage passing as a function of the item’s mental-age placement in the original standardization sample is a nearly perfect ogive of the normal curve. Thus the S-B item difficulties generally maintain the same relative positions in the 1963 black sample as in the 1937 white standardization sample.

Contrasting Tests: Picture Vocabulary and Matrices. ... Item difficulty in a culture-loaded test such as the PPVT is highly related to the rarity of the item, that is, the frequency or probability of encountering the informational content of the item in the so-called core culture in which the test was devised and standardized. Thus there is a close correspondence between the rank order of difficulty of the PPVT items and the rank order of the frequency of occurrence of the stimulus words (per million words) in American newspapers, magazines, and books (Jensen, 1974a, pp. 192-194) showing that PPVT item difficulty is closely related to the degree of rarity of the words in general usage in American English (see Figure 11.3). Rarity, more than complexity of mental processes, determines the difficulty of PPVT items. [...]

Item difficulty in a nonverbal culture-reduced test such as the Raven depends on the complexity of the items (abstract figural material) and the number of elements involved in the reasoning required for the correct solution.

It should be instructive, therefore, to compare the PPVT and the Raven with respect to the analysis of item x group interaction. I have done this with large representative samples of elementary school children from three ethnic groups (white, N = 638; black, N = 381; Mexican-American, N = 644) in a California school district. The study was replicated for the Raven in grades 3 to 8 in another California school district, with representative samples of 1,585 whites, 1,238 blacks, and 1,396 Mexican-Americans. Replication with the PPVT and Raven in still another California school district involved only whites (N = 144) and blacks (N = 144) in grades K, 1, and 3, randomly drawn from the two most contrasting neighborhood schools in the whole country with respect to socioeconomic status. The details of all these studies are presented elsewhere (Jensen, 1974a).

Item bias was examined both by means of cross-group correlation of item difficulties and by the item x group interaction in the analysis of variance.

The item difficulties (p values) of the PPVT and Raven were rank order correlated between ethnic groups, with the results in the various studies shown in Table 11.19. These correlations, which are not corrected for attenuation, are all very high. The average correlation between males and females within each of the ethnic groups is shown for comparison; the correlations indicate that there is no greater item x ethnic group interaction than item x sex (same ethnicity) interaction. The Raven has consistently higher correlations than the PPVT, as one might expect, but the difference is practically negligible. The lowest correlations were obtained in the white and black groups selected at the extremes of socioeconomic status, but it should be noted that these correlations are based on smaller samples and on fewer items (because of the smaller range of p values larger than zero).

There are a number of indications that the “lowness” of these extremely high correlations is due mostly to the groups’ overall differences in ability levels. When the Raven p values are determined within each school grade separately, it is seen from the white-black cross-racial x cross-grade correlations of the p values that whites resemble blacks who are two grades higher (i.e., about two years older) more than they resemble blacks of the same age or other whites who are two years older. In fact, grade 4 whites are more like grade 6 blacks (r = .98) than grade 4 whites are like grade 6 whites (r = .81). This result seems much less consistent with the hypothesis of a cultural difference than with the hypothesis of a difference in rates of intellectual development, unless we make the unlikely assumption that the test manifestations of cultural differences are indistinguishable from the test manifestations of general developmental difference within a culturally homogeneous group.

Another indication that the Raven item x group interaction is more a function of developmental lag than of cultural differences per se was obtained by factor analyzing the intercorrelations among all the Raven items and then getting the cross-racial x cross-grades correlations between the items’ loadings on the first principal component. Blacks and whites in grade 4 correlate .52, but grade 4 whites and grade 5 blacks correlate .65, and grade 4 whites and grade 6 blacks correlate .85. The Mexicans do not fit this developmental lag hypothesis; they show their highest correlation for item factor loadings with whites of the same grade level: for example, grade 4 whites and grade 4 Mexicans correlate .75, whereas grade 4 whites and grade 6 Mexicans correlate -.02.

The group x item interaction in the analysis of variance gives essentially the same picture of these data. Also, it was possible to simulate quite closely the results of the white-black ANOVA for both PPVT and Raven by making up pseudorace groups composed entirely of younger (ages 6 to 9 years) and older (ages 8 to 11 years) whites. The simulation was not quite as good in the case of Mexicans. The values of eta squared x 100 (i.e., the percentage of the total variance accounted for) of the item x group interaction in the ANOVA of the PPVT and the Raven are as shown in Table 11.20. Note that by comparing younger white with older ethnic groups we can appreciably reduce the size of the item x group interaction as expressed by eta squared. An interaction quite comparable to that found in the white-black ANOVA is produced by doing an ANOVA on older and younger whites (i.e., the pseudorace comparison).

The interaction ratios, GD/I (see pp. 561-562), which indicate the magnitude of the group mean difference on the test as a whole relative to the item x group interaction, are as follows:

Groups in ANOVA                                              PPVT        Raven
White and black                                                   7.10          17.32
White and Mexican                                             8.55         18.13
White (ages 6-9) and white (ages 8-11)           7.97          18.26

Note that the GD/I ratios for the Raven are more than double those for the PPVT. This is what we should expect in comparing the GD/I ratio of a culture-reduced test with that of a culture-loaded test, if the mean group difference is real and not an artifact of test bias. Yet the ratios are very high for both the Raven and the PPVT and indicate that no amount of item elimination or sampling of other items from the same general population of such items would stand a chance of equalizing or reversing the white-black or white-Mexican mean difference on either test. These high GD/I ratios reflect the fact that the direction of the majority-minority difference is not reliably reversed on any item in either the PPVT or the Raven.

It should be interesting to see how much we can reduce the majority-minority difference on the PPVT by selecting from among the 150 PPVT items those that discriminate the majority-minority groups the least, as compared with those that discriminate the most. I made up separate subtests of the two types of items, then compared the majority-minority mean differences on the most and the least discriminating subscales. The PPVT subscale made up of the thirty-three items with the highest white-black discrimination showed a mean white-black difference of 1.28σ; the subscale composed of the thirty-one least discriminating items showed a mean white-black difference of 1.07σ. (The corresponding figures for the most and least discriminating subscales for the whites versus Mexican contrasts are 1,79σ and 1.45σ.) All these mean differences expressed in σ units are actually larger than the mean majority-minority differences on the full PPVT expressed in σ units, since the specially contrived subscales have considerably smaller within-group standard deviations. The most and least discriminating subscales correlate with each other .91 (for the black scales) and .88 (for the Mexican scales) in the combined ethnic groups. When Spearman-Brown corrected for length of the test, these correlations between subscales are as high as the split-half reliabilities of the whole PPVT, indicating that the two subscales still measure the same ability as the whole PPVT. Also, the most and least discriminating PPVT subscales show approximately the same correlations (averaging .63) with total scores on the Raven, which is further evidence that the most and least ethnically discriminating PPVT items are factorially equivalent.

Another investigation comparing the rank order of PPVT item difficulties in random samples of fourth- and fifth-grade white and black children enrolled in regular classes in the public schools in Middletown, Connecticut, found “no statistically significant difference in the correlation between item order and item difficulty for groups of different race or sex” (Berry, 1977, p. 40).

Thus we see that even the highly culture-loaded PPVT shows only slightly more item bias, as revealed by indices of items x ethnic groups interaction, than the culture-reduced Raven; and neither test shows any appreciable item bias for large samples of American-born black and Mexican-American children. The scant item x group interaction that exists is largely attributable to group differences in overall level of ability on the tests and can be simulated by comparing ethnically homogeneous groups of older and younger children. If culture bias is claimed to exist for these tests in these groups, it must also be argued that the bias involves all the items of the PPVT and the Raven about equally. This seems unlikely for a cultural effect in any meaningful sense of the term; the uniformity of the group differences across virtually all items of these tests seems more likely attributable to other factors - factors that could be reasonably hypothesized to have a much more general influence on overall rate of mental development.

Chapter 12 External Sources of Bias

Race of Examiner

Adequate and Complete Designs

Jensen (1974c): Twelve white Es and eight black Es administered four group tests to all the white and black children (about 5,400 whites and 3,600 blacks) from kindergarten through sixth grade in the public schools of Berkeley, California. The tests are the Lorge-Thorndike (Verbal and Nonverbal) Intelligence Test, Figure Copying, Memory for Numbers (digit span), Listening-Attention Test, and Speed and Persistence Test (Making Xs). Analysis of variance was performed on each test at each grade level and also averaged over all grades. Because the sample sizes are very large, even quite small effects are significant. The Lorge-Thorndike Nonverbal IQ shows no overall race of E x race of S interaction, but the interaction is significant for Verbal IQ, although the net effect of the interaction amounts to only 3.2 percent (or less than 1 IQ point) of the mean white- black difference in Verbal IQ. The Figure Copying Test (a measure of g) shows a significant interaction amounting to 11.4 percent of the mean white-black difference. The Speed and Persistence Test, a measure of motivation or effort in the testing situation, showed a significant interaction amounting to more than the mean white-black difference, which does not differ significantly from zero on this test. White Es elicited significantly better performance from white Ss than from black Ss. The Listening-Attention Test and Memory for Numbers Test both show a nonsignificant main effect for race of E and for the interaction of race of E x race of S. Conclusions were as follows:

The present results on group-administered tests . . . show unsystematic and, for all practical purposes, probably negligible effects of race of E on the mental test scores of the white and black school children. Moreover, the direction of the relatively slight race of E effects does not consistently favor Ss of either race. The magnitudes of race of E effects are in all cases very small relative to the mean difference between the racial groups, except for the one noncognitive test, Making Xs, which is a measure of motivation or speed and persistence under the conditions of group testing. On this test, both white and black 5 in all grades performed significantly and substantially (about 0.4 to 0.8σ) better with white Es than with black Es. This shows that some types of performance are capable of systematically reflecting race of E effects and it tends to highlight the relative lack of such effects on the cognitive ability tests. (Jensen, 1974c, p. 12)

As a part of the same study (but not reported in Jensen, 1974c), one subject was selected at random from each classroom in the Berkeley schools to be tested individually on the Lorge-Thorndike IQ Test by either one of the white Es or one of the black Es. Analysis of variance showed a nonsignificant main effect of race of E for both nonverbal and verbal IQ and a nonsignificant race of E x race of 5 interaction for nonverbal IQ, but a significant (p < .01) interaction for verbal IQ. The interaction, however, works just the opposite of the popular expectation: the mean white-black difference in verbal IQ is greater (by 3.2 IQ points) when the Ss are tested by Es of their own race than when tested by Es of a different race.

Language and Dialect of Examiner

Black Dialect. Many blacks, particularly those from poor socioeconomic backgrounds, speak a nonstandard dialect distinctly different from standard English. Therefore it seems plausible that some part of the average difference between blacks and whites on mental tests might be attributable to the discrepancy between the dialect to which black Ss are accustomed and the standard English spoken by the examiner (E), whether the E is black or white. Deficient performance on a test could result from the S’s failure fully to understand either the E’s oral directions or the verbal test items themselves when presented in standard English.

The consensus of a number of studies, however, indicates that, although black children produce somewhat different speech, they comprehend standard English at least as well as they comprehend their own nonstandard dialect and that they develop facility in understanding the standard language at an early age (Eisenberg, Berlin, Dill, & Sheldon, 1968; Hall & Turner, 1971, 1974; Harms, 1961; Krauss & Rotter, 1968; Peisach, 1965; Weener, 1969).

The effect of black dialect as compared with standard English on the IQs of black lower-class children was investigated in three studies by Quay (1971, 1972, 1974), who had the Stanford-Binet translated into black ghetto dialect by a linguistics specialist in black dialect. No significant difference (the difference actually amounts to less than 1 IQ point) was found between the nonstandard dialect and standard English forms of the Stanford-Binet when administered by two black Es to one hundred black children in a Head Start program in Philadelphia (Quay, 1971). The same results were found in a second study in which black 4-year-olds were obtained from “an extremely deprived, physically and socially isolated community” (Quay, 1972). Moreover, in this study the item difficulties (i.e., percentage passing each item) of the individual Stanford-Binet items were compared for the two versions of the test, the dialect version and the standard version. The two versions showed no significant differences in item difficulties. In Quay’s third study, essentially the same procedure was repeated, but this time 104 Philadelphia black children at two age levels (grades 3 and 6) were tested to ascertain whether the language condition (dialect versus standard English) might show an interaction with Ss’ age. Ss’ sex was also taken into account in the 2 (language) X 2 (age level of S) X 2 (sex of S) design. The only significant effect in the ANOVA is Ss’ age, with the younger Ss having higher IQs. Not E’s language (black dialect versus standard English), or S's sex or the interaction of S’s language x S’s sex is significant. The black dialect and the standard English forms of the Stanford-Binet yielded mean IQs of 84.58 (σ = 10.47) and 84.52 (σ = 11.08), respectively. Item difficulties (proportion passing) were compared across the language conditions; six out of seventy-two comparisons showed significant (p < .05) differences, but about four significant differences would be expected by chance. On three of these significant differences black dialect was easier, and on the other three standard English was easier. Quay interpreted all these differences as due to chance, as they are inconsistent in direction and occur haphazardly on the nonverbal as well as on the verbal items. Quay concluded that black children are not penalized by the use of standard English in test administration.

In a factorial design, Crown (1970) varied not only the language of test administration (black dialect versus standard English), but also the race of E (two black Es and two white Es) and the race of S (twenty-eight black and twenty-eight white kindergartners in Florida) on the Wechsler Preschool and Primary Scale of Intelligence. ANOVA reveals no significant difference overall between the black dialect and standard English conditions, and there are no significant interactions of language with race of E or race of S.

Bias Arising from Motivational, Attitudinal, and Personality Factors

Test Anxiety. There is a considerable literature on the role of anxiety in test performance. The key references to this literature are provided in reviews by Anastasi (1976, pp. 37-38), Matarazzo (1972, pp. 439-449), I. G. Sarason (1978), S. B. Sarason et al. (1960), and Sattler (1974, p. 324). In brief, many studies have reported generally low but significant negative correlations between various measures of the subject’s anxiety level, such as the Taylor Manifest Anxiety Scale and the Sarason Test Anxiety Scale, and performance on various mental ability tests. Many nonsignificant correlations are also reported, although they are in the minority, and are usually rationalized by the investigators in various ways, such as atypical samples, restriction of range on one or both variables, and the like (e.g., Spielberger, 1958). I suspect that this literature contains a considerably larger proportion of “findings” that are actually just Type I errors (i.e., rejection of the null hypothesis when it is in fact true) than of Type II errors (i.e., failure to reject the null hypothesis when it is in fact false). Statistically significant correlations are more often regarded as a “finding” than are nonsignificant results, and Type I errors are therefore more apt to be submitted for publication. Aside from that, sheer correlations are necessarily ambiguous with respect to the direction of causality. Persons who, because of low ability, have had the unpleasant experience of performing poorly on tests in the past may for that reason find future test situations anxiety provoking - hence a negative correlation between measures of test anxiety and ability test scores.

Test anxiety has not figured prominently among the variables hypothesized to account for cultural or racial group differences in test scores. The lack of published studies on this point, in fact, further strengthens the suspicion that null results are seldom reported when found. Yet the few null results that are published are quite clear-cut.

For example, one of the most sensitive indicators of anxiety level is pulse rate, and we note that the Sarason Test Anxiety Scale contains the item “I sometimes feel my heart beating very fast during important tests.” Noble (1969) measured the pulse rates of groups of white and black elementary school children immediately before and after being individually tested and found no race difference in pre- or posttest pulse rate.

The Sarason Test Anxiety Scale given to black and white children between the ages of 8 and 11 showed no significant race difference, no significant interactions with S’s race x E’s race, and no significant correlations with WISC Full Scale IQ (Solkoff, 1972).

A questionnaire measure of manifest anxiety, the N (neuroticism) scale of the Junior Eysenck Personality Inventory, administered to large samples of white, black, and Mexican-American children in grades 4 to 8 in a California school district, showed significant but very small (less than 1 point) group differences, with whites having higher anxiety scores. In all groups the N scale showed nonsignificant and negligible correlations with verbal and nonverbal IQ and tests of scholastic achievement (Jensen, 1973e).

Among the various subtests of the Stanford-Binet and the Wechsler IQ tests, digit span is generally claimed to be the most sensitive to the adverse effects of anxiety, which interferes with the subject’s concentration and short-term retention. An enforced 10-second delay in recall depresses digit-span retention, due to the interference of extraneous thoughts, which are presumably increased by test anxiety. (For example, the Test Anxiety Scale contains items expressing this form of distractability while taking a test.) Therefore it was predicted that, if whites and blacks differ in test anxiety, there should be an interaction between race and immediate versus delayed recall of aural digit series. No significant interaction was found in the digit-span performance of white (N = 4,467) and black (N = 3,610) California school children in grades 2 to 8 (Jensen & Figueroa, 1975).