Educability and Group Differences (Jensen, 1973)

I scanned “Educability and Group Differences” (Arthur Jensen, 1973). A PDF version is now available here. For this post, I selected some enlightening passages of the book (see below).

CONTENT [Jump links below]

Ch.2 Technical Misconceptions and Obfuscations
Ch.3 Intelligence and Educability
Ch.4 Heritability of Scholastic Achievement
Ch.6 Social Class Differences in Intelligence
Ch.7 Race Differences in Intelligence
Ch.8 Multiple and Partial Correlation Methods
Ch.9 Intelligence of Racial Hybrids
Ch.11 Equating for Socioeconomic Variables
Ch.12 Accentuated Environmental Inequalities
Ch.13 Inequality of Schooling
Ch.14 Teacher Expectancy
Ch.15 Motivational Factors
Ch.16 Language Deprivation
Ch.17 Culture-biased Tests
Ch.18 Sensori-motor Differences
Ch.19 Physical Environment and Mental Development

Chapter 1

Subpopulation Differences in Educability

OBSTACLES TO CLEAR THINKING ON THIS TOPIC

… In noting that certain personality variables, when factor-analyzed along with tests of mental abilities, were correlated to the extent of about 0.3 to 0.5 with a general ability factor, R. B. Cattell (1950, pp. 98-9) commented that ‘. . . there is a moderate tendency . . . for the person gifted with higher general ability, to acquire a more integrated character, somewhat more emotional stability, and a more conscientious outlook. He tends to become “morally intelligent” as well as “abstractly intelligent.”’

Chapter 2

Technical Misconceptions and Obfuscations

TEACHABILITY AND HERITABILITY

The fact that scholastic achievement shows lower heritability than IQ means that more of the variance in scholastic achievement is attributable to non-genetic factors than is the case for IQ. … By the same token, low heritability does not guarantee that most of the nongenetic sources of variance can be manipulated systematically. A multitude of uncontrollable, fortuitous micro-environmental events may constitute the largest source of phenotypic variance in some traits, so that although they have low heritability, they are even much less potentially controllable than if the heritability were very high, at least permitting sure control through genetic selection.

THE FALLACY OF ASSUMING GENETIC HOMOGENEITY WITHIN RACIAL GROUPS

… The argument from regional differences among whites as entirely environmental to differences between racial groups as entirely environmental might be called the Klineberg fallacy, since it was Otto Klineberg (1935, 1944) who first popularized the comparison of Army Alpha test scores of whites in four Southern states, where the white Alpha test scores of whites in four Southern states, where the white Alpha medians were the highest in the nation for Negroes. (The four highest Negro medians were well above the four lowest white medians. Comparison of Negro and white medians within the same state, on the other hand, showed about the same difference as for the average Negro-white difference in the nation as a whole.) … The fact that the Army Alpha is highly loaded with scholastic knowledge, correlating close to 0.70 with number of years of schooling, means that it probably reflects regional differences in mean level of education to some degree, independently of intelligence, especially in the period of World War I, when there was much greater regional variance in the quality and the number of years of schooling than exists at the present time. [...]

Coming back now to the point made by Klineberg, that there are regional differences in test scores among both racial populations, we can view the current situation by comparing the results obtained in various states.

Highest percent of failures in any state:
White = 9.7 percent (Tennessee)
Negro = 46.7 percent (Mississippi)
Sigma difference = 1.12σ ≈ 16.8 IQ points.

Second-highest percent of failures in any state:
White = 9.4 percent (Kentucky)
Negro = 42.7 percent (Tennessee)
Sigma difference = 1.13σ ≈ 16.9 IQ points.

Lowest percent of failures in any state:
White = 0.6 percent (Rhode Island)
Negro = 7.4 percent (Wisconsin)
Sigma difference = 1.06σ ≈ 15.9 IQ points.

Second-lowest percent of failures in any state:
White = 0.9 percent (Minnesota)
Negro = 11.1 percent (California)
Sigma difference = 1.29σ ≈ 19.4 IQ points.

Comparison of highest white and lowest Negro failure rates:
White = 9.7 percent (Tennessee)
Negro = 7.4 percent (Wisconsin)
Sigma difference = 0.15σ ≈ 2.25 IQ points (in favor of Negroes).

Comparison of lowest white and highest Negro failure rates:
White = 0.6 percent (Rhode Island)
Negro = 46.7 percent (Mississippi)
Sigma difference = 2.43σ ≈ 36.45 IQ points.

Comparison of second-highest white and second-lowest Negro failure rates:
White = 9.4 percent (Kentucky)
Negro = 11.1 percent (California)
Sigma difference = 0.11σ ≈ 1.65 IQ points (in favor of whites).

Thus, we see that in contrast to the data noted by Klineberg from World War I, when the Negro medians of four Northern states exceeded the white median of four Southern states, in 1968 there are only two pairs of states (Tennessee and Wisconsin, and Kentucky and Wisconsin) in which Negroes obtain higher AFQT scores, on the average, than whites. In this 1968 sample, the mean score of white males in Tennessee would correspond to 95, i.e., 5 points below the whites’ national average, on an IQ scale, while the mean score of Negro males in Wisconsin would be 97.25, i.e., nearly 13 points above the Negroes’ national average.

Since the AFQT is clearly predictive of individuals’ capabilities in learning and performance in the armed forces, the above figures must give pause concerning the capabilities of Negroes, on th average, for competing with other subpopulations educationally and occupationally outside the armed forces. Whatever the causes, the facts themselves cannot be taken lightly. Reviews of the evidence on the predictive validity of IQ and aptitude tests indicate that such tests have the same validity for Negroes and whites for predicting educational performance (Stanley, 1971; Sattler, 1972).

Why has the number of Northern states with Negro means higher than white means in Southern states decreased from World War I to the present time – a period marked by educational and economic advances for the whole population and especially for Negroes? The increasing migration of Negroes from the rural South to the urban North is the most likely explanation. Generally the first migrants are selected for superior abilities and physical characteristics which is not the case with later migrants. Negroes who migrated North prior to World War I probably represent a different selection of Southern Negroes from those who migrated North after World War II. In World War II, the percentage of Southern Negroes who failed the Army General Classification Test was consistently greater than for Northern Negroes, even when matched for amount of formal education, from less than five years of schooling up to the college level. Northern Negroes constituted nearly one-third of all Negroes accepted into the armed forces in World War II, although they consituted less than a fourth of all Negro registrants (Stouffer et al., 1965, pp. 493-4). [...]

But perhaps the more serious consequences of the 1σ mean difference are at the lower extreme of the distribution. Persons who have been exposed to schooling for several years but who still have IQs below 70, especially on non-verbal and non-scholastic tests, are severely handicapped in the world of work, and can be seldom succeed in any kind of skilled or semi-skilled work available in an industrial society. Most of them have difficulty finding employment in an urban economy and they are frequently dependent either upon relatives or public welfare for their support. Persons in our society today with IQs below 70 are generally regarded as mentally retarded and in school would be recognized as such even if there were no IQ tests. This degree of handicap cannot be passed off lightly as a ‘cultural difference,’ because the behavioral correlates of an IQ below 70 are probably a handicap in any modern culture. … If the quality of the environment depends to some extent upon the intelligence of the persons who create the environment, we cannot argue, as some social scientists would do, that subpopulation intelligence differences can only be studied after complete environmental equality has been achieved, in which case presumably all differences would be eliminated and there would no longer be a problem calling for solution.

NOTES

11. Most white-Negro mean differences reported in the literature probably underestimate the true population difference because of a statistical artifact that enters into any comparison between two groups which are not sampled from the total range or scores in the population, as when samples are drawn from schools or the armed forces which may exclude IQs below some rather low selection cut-off. If on some metrical trait x two normally distributed populations differ by some amount d, and if samples are drawn only between the values a and b (i.e., the sample is restricted to the range of values a < x < b), then the lower group is always favored, i.e., d is always underestimated or, in other words, the sample means differ less than the population means. The same thing is true if sampling is restricted only by an upper or a lower selection cut-off.

Chapter 3

Intelligence and Educability

Much of what is tapped by IQ tests is acquired by incidental learning, that is to say, it has never been explicitly taught. Most of the words in a person’s vocabulary were never explicitly taught or acquired by studying a dictionary. Intelligence test items typically are sampled from such a wide range of potential experiences that the idea of teaching intelligence, as compared with teaching, say, reading and arithmetic, is practically nonsensical.

The items in a vocabulary test are sampled from such an enormously large pool of potential items that the number that can be acquired by specific study and drill is only a small proportion of the total, so that few if any of the words one would acquire in this way are likely to appear in any given vocabulary test. Moreover, persons seem to retain only those words which fill some conceptual ‘slot’ or need in their own mental structures. A new word encountered for the first time which fills such a conceptual ‘slot’ is picked up and retained without conscious effort, and it will ‘pop’ into mind again when the conceptual need for it arises, even though in the meantime the word may not have been encountered for many months or even years. If there was no conceptual slot that needed to be filled, that is to say, no meaning for which the individual has a use and which the word serves to symbolize, it is exceedingly difficult to make the definition of the word stick in the individual’s memory. Even after repeated drill, it will quickly fade beyond retrieval.

Teaching of the skills before the necessary maturation has occurred is often practically impossible, but after the child has reached a certain age successful performance of the skill occurs without any specific training or practice. The items in scholastic achievement tests do not show this characteristic. For successful performance, the subject must have received explicit instruction in the specific subject matter of the test. The teachability of scholastic subjects is much more obvious than of the kinds of materials that constitute most intelligence tests and especially non-verbal tests.

GROWTH MODEL OF ACHIEVEMENT

Among the most interesting and theoretically important facts about scholastic achievement are the manner in which it increases or ‘grows’ over the years and the particular pattern of intercorrelations of individual differences in achievement from year to year over the course of schooling from first grade to high school graduation. In these aspects, the growth of scholastic knowledge closely resembles the growth of intelligence, and also, interestingly enough, it resembles the essential features of growth in physical stature. Total vocabulary size, one of the best indices of intelligence that can be measured on an absolute scale, also shows the same growth characteristics. The evidence relevant to the following discussion is derived from longitudinal studies in which the achievements of the same children are measured each year over the course of their schooling. Much of this evidence has been compiled by Benjamin Bloom (1964).

In the growth of scholastic knowledge and competence, just as in the growth of intelligence and of physical stature, individuals fluctuate in relative standing among their age peers throughout the course of development. The individual year-to-year fluctuations in relative standing are greater early in development and gradually diminish as individuals approach maturity. The year-to-year intercorrelations of scholastic achievement show a highly distinctive pattern. I have examined virtually all such longitudinal correlation matrices for achievement reported in the literature and have found no exception to this distinctive pattern.

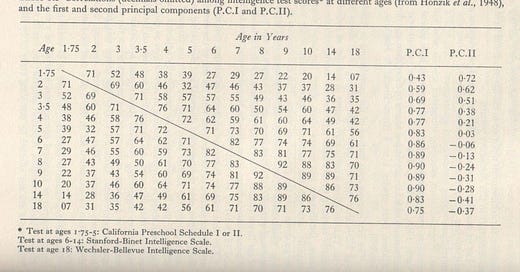
Let us examine a couple of tables of actual correlations among year-to-year achievement measures. Table 3.1 shows the intercorrelations among standardized achievement scores of 272 white and Negro children attending integrated schools who had been tested at each grade level from 3rd grade to high school (from Vane, 1966, Table 1). Table 3.2 shows the year-to-year intercorrelations of achievement test scores of more than one thousand children from grades 1 to 9 (from Bracht & Hopkins, 1972, Table 2).

The first conspicuous feature of the correlations in Table 3.1 and 3.2 is that they are quite high, ranging from about 0.60 to 0.90. This indicates a fairly high degree of stability of individuals’ relative standing in scholastic achievement throughout the school years. Intelligence test scores show about the same degree of stability, although the correlations span a much wider range as we go into the pre-school years. This can be seen in Table 3.3, which shows the intercorrelations among intelligence test scores of some 200 children from age 1.75 years of age to 18 years of age (from Honzik, MacFarlane, & Allen, 1948, Table III). Here the correlations range from close to zero (between ages 1.75 years and 18 years) up to about 0.90.

The most striking feature of all three correlation matrices, however, is the pattern of correlations, with the size of the correlations being largest near the principal diagonal and decreasing more or less regularly the further away they are from the diagonal. That is to say, the intercorrelations for temporally adjacent tests are high, and there is a regular decline in correlations as the interval between tests increases. All longitudinal test data on intelligence, vocabulary acquisition, physical stature, and scholastic achievement, it so happens, conform to this pattern when the measures are intercorrelated. Guttman (1954) has called this pattern of correlations a simplex. This point is worth knowing, because a simplex can be accounted for in terms of a very neat and simple model.

Before this model is described, a word is in order about the factor analysis or principal components analysis of a correlation matrix which is a simplex. A perfect simplex (i.e., one in which the correlations are not affected by sampling error or by differences in test reliability), when subjected to a principal components analysis that extracts as many components (i.e., hypothetical independent sources of variance) as there are tests, will yield (1) a large general factor (the first principal component), (2) a bipolar factor with positive loadings on early tests and negative loadings on late ones, (3) a factor that plots a U with negative loadings in the middle of the series, (4) a factor with loadings that plot out a sine curve, and (5) a number of remaining nondescript, random factors (equal to the number of tests minus 4) which account for smaller and smaller proportions of the total variance among all the tests. In practice one applies some criterion for the number of components to be extracted (such as having Eigenvalues greater than 1), since each successive component accounts for less and less of the total test variance and beyond a certain point the components do not account for a significant percentage of the variance. In most of the correlation matrices of longitudinal intelligence and achievement data in the literature, only the first principal component has an Eigenvalue greater than 1 and it usually accounts for more than three-fourths of the total variance. The first principal component by definition is the one factor which accounts for most of the variance in all the tests, and in a simplex it is very large indeed, for as we shall see, there is really only one common factor plus as many random factors as there are tests in a simplex. The last column in Table 3.1 and 3.2 shows the correlation of the achievement tests at each grade with the first principal component, which in both Table 3.1 and Table 3.2 accounts for 82 percent of the variance. In Table 3.3 the first two principal components had Eigenvalues greater than 1 and were therefore extracted; they account for 62 percent and 15 percent of the variance, respectively.

What kind of model will produce a simplex? Only two basic elements are required: [1] (1) a rate of consolidation factor, C, on which individuals maintain their relative positions in the population over the course of development, and (2) a random increment or gain, G, from time x to time x+1 (t_x to t_x+1). An individual’s status, S, at any given time consists of the sum of C x G over all previous time plus the G of the immediate past. In effect, the consolidation factor C is a positive constant for a given individual; the gain factor G is a positive random variable in each time interval t_x – t_x+1. An individual’s growth curve can then be represented as follows:

t₁ : G₁ (Gain since t₀ )
t₂ : CG₁ + G₂ = S₂ (Consolidated gain from time 1 to time 2 plus unconsolidated gain at time 2 = status at time 2.)
t₃ : CG₁ + CG₂ + G₃ = S₃
t₄ : CG₁ + CG₂ + CG₃ + G₄ = S₄
t_n : C (G₁ + G₂ + G₃ + G₄ + … + G_n-1) + G_n = S_n

For some measures, like height, one can never observe in the measurements themselves the gain G but only the consolidated gain CG, so that one always finds S₁ < S₂ < S₃, etc. This is not always the case for other characteristics such as the growth of body weight during development or the growth of intelligence or of scholastic achievement.

An actual simplex can be created simply by assigning some numerical values to C and G. Simulated individuals, for example, can each be assigned a C value selected from randomly distributed numbers from 0.10 to 1.00, and at each point in time G will be some value from 0 to 9 also taken from a table of normal random numbers. (To produce a growth curve which does not increase linearly but logarithmically, i.e., at a negatively accelerated rate characteristic of most growth curves, one can simply use the natural logarithm of S at each point in time. This will produce a quite typical looking growth curve, but the form of the growth function is not an essential aspect of the simplex. In the absence of an absolute scale, as is true of most psychological measurements, the form of the average growth curve, aside from being an increasing monotonic function of time, is quite arbitrary. The growth of vocabulary, a good index of intellectual development, can be measured on an absolute scale [number of words] and appears to be sigmoid. Over the period of schooling, from about age 5 to 18 years, however, the growth curve of vocabulary is logarithmic.) The S values at times t₁, t₂, t₃, etc. for 100 or more such simulated individuals when intercorrelated yield a correlation matrix with the simplex pattern. More complicated models can also produce a simplex; but this is the simplest model that will do it. The resulting simulated correlation matrix is virtually indistinguishable from those obtained from actual longitudinal intelligence and achievement test data.

Can we make a reasonable psychological interpretation of this model? The S values, of course, are no problem; they are simply the achievement measurements taken at different times. They are composed of consolidated gains, CG, plus unconsolidated gains, G, plus random errors of measurement, e.

The consolidation factor, C, is a variable which is more or less intrinsic to the individual; it is that aspect of individual differences in S values in the population at any cross-section of development which may be attributed to genetic and constitutional factors (which are not distinguishable in this model per se). The term consolidation as used here does not refer to the consolidation of short-term memory traces into long-term storage, but to the assimilation of experience (i.e., learning) into cognitive structures which organize what has been learned in ways that subsequently permit quick and adequate retrieval and broad transfer of the learning in new relevant situations. Stated in simplest terms, C is the process of understanding what one has learned. It is ‘getting the idea’, ‘catching on’, having the ‘Aha!’ experience that may accompany or follow experiencing or learning something, and the relating of new learning to past learning and vice versa. When learning takes place without C acting upon it, it is less retrievable and much less transferable for use in solving problems that are more or less remote from the original learning situation. C is what is generally meant by the term intelligence, but it can be manifested, observed, and measured only through its interaction with experience and learning. There can be learning without intelligence (i.e., without C) but intelligence cannot be manifested without learning. In our simple model we have represented the capacity for consolidation as a constant value for each individual; this is not an essential feature, although a more or less constant rank order of individuals’ C values is essential. On the average, over the life span the C value probably increases up to maturity, levels off at maturity, and gradually declines in old age. Our concept of C comes very close to R. B. Cattell’s concept of fluid intelligence. All intelligence tests measure S, but some tests reflect more of the C component (which Cattell would call tests of fluid intelligence) and some reflect more of the G component (which Cattell would call tests of crystalized intelligence) (see Cattell, 1971, ch. 5).

The gain factor, G, consists of experience or learning and unconsolidated (or rote) memory of such learning. But is G properly represented as a random variable in our model? Consider the following quite well-established empirical findings. Learning abilities (which do not involve problem solving) have been found to show quite low, often negligible, correlations with intelligence. (For an excellent review, see Zeaman and House, 1967.) Moreover, a general factor of learning ability has not been found. There is a great deal of situation-specific or task-specific variance in learning, making for very low or even zero correlations among various kinds of learning. Therefore, learning per se in the vast variety of conditions under which it occurs in real life, cannot show much correlation, if any, with relatively stable individual difference variables such as intelligence.

Furthermore, consider the relative unpredictability or randomness of the individual’s day-to-day experiences or opportunities for learning this or that, and the poorly correlated other variables, such as attention, motivation, and persistence, that can affect learning at any given moment. All these factors within a given interval of time add up in effect to a more or less random variable. It should be understood that random does not mean uncaused. A child may go down with measles and have to stay out of school for ten days and so miss out on a good many school learning experiences. Another child may miss out for a few weeks because his family moves to another city. … The gains (or lack of gains) in any short period, though caused by a multitude of factors, appear in effect to be more or less random in the school population.

In his detailed and penetrating analysis of the mental test data of the Harvard Growth Study, Robert L. Thorndike (1966) noted that ‘In considerable part, the factors that produce gains during a specified time span appear to be different from those that produced the level of competence exhibited at the beginning of the period.’ Thorndike reports the typical correlation between initial status and gain for a one-year interval to be +0.10, which is about +0.22 when corrected for attenuation. That is to say, initial status and gain after one year have less than 5 percent of their variance in common. (In Thorndike’s analysis, status and gain were measured by experimentally independent measures, i.e., equivalent forms of the test, in order to avoid common errors of measurement lowering the correlation. One form of the test was used as the measure of initial status and an independent equivalent form was used as the base from which gains were computed.) This finding is consistent with the simplex model. Very little of the gain in a year’s interval becomes consolidated as status. If it did, we should expect a much higher correlation between independent measures of status and of gain. Moreover, if a large random element did not enter into the short-term gains we should expect consistent individual differences in gains from one interval to the next and consequently substantial correlations between grains from one interval to the next. But this in fact is not the case. Thorndike gives the average correlation between two independent gain scores on intelligence tests for different intervals:

1-year interval = 0.101
2-year interval = 0.240
3-year interval = 0.266
4-year interval = 0.188
5-year interval = 0.265

The longer the interval, of course, the larger is the proportion of the gain that has been consolidated and therefore the larger the correlations between gains over longer intervals. The same effect is reflected in the average correlations of initial status with gain based on experimentally independent tests:

1-year interval = 0.045
2-year interval = 0.006
3-year interval = 0.031
4-year interval = 0.139
5-year interval = 0.329

These actual correlations are even smaller and somewhat less regular than would be predicted from the simplex model, probably because of measurement error, slightly changing factorial composition of the tests at different levels of difficulty (and thus at different ages), and unequal units of measurement over the full range of scores.

Another fact to be considered in this model is the heritability of the trait under consideration. This is quite high for intelligence and vocabulary, but lower for scholastic achievement, particularly in the elementary grades and for subjects such as spelling and mechanical arithmetic. Of all the growth characters on which there are good data, the highest heritability is for height. What high heritability means, among other things, is that a large part of the variance in status on the trait at maturity is, in principle, predictable at the moment of conception. That is to say, it is determined by genetic factors. If we take into consideration prenatally determined constitutional factors as well as the genetic factors, most of the variance in adult status for highly heritable characteristics like height, and to a slightly lesser degree intelligence, is theoretically predictable at birth. When something is highly predictable, it means nothing less than that it is predetermined. This is an unpopular but nevertheless accurate meaning of predictability. Predictability does not necessarily imply, however, that we have any control over the predetermining factors, nor does it necessarily imply the contrary. Although the correlation between Stanford-Binet IQ at age 2 and at age 18 is not higher than about +0.3, meaning that less than 10 percent of the variance in IQs at age 18 is predictable from a knowledge of IQs at age 2, heritability estimates indicate that some 70 to 80 percent of the variance in adult IQs is, in principle, predictable or predetermined at the moment of conception. At each year from birth on, more and more of the predictable, predetermined aspect of the phenotype becomes manifest. This assumes, of course, that environmental influences throughout the course of children’s development are no more variable than the actual environments in which the vast majority of children in our society are reared. It is the consolidation factor, C, in our simplex model which corresponds to the genetic and constitutional determining factors. Thus we should expect from this model that the heritability of IQ should increase from infancy to maturity as more and more experience is consolidated. This has been found in the increase of parent-child correlations from infancy to later childhood; such correlations strongly reflect heritability when the children have had no contact with their natural parents (because of adoption) with whom they show increasing correlations in intelligence as they mature, as was shown by Honzik (1957).

Also, from our model we would expect the squared loadings of the first principal component of the simplex matrix (P.C.I in Tables 3.1, 3.2, and 3.3) to approximate the amount of variance accounted for by individual differences in the C factor at any cross-section in the time scale of development. This can be clearly shown with simulated data in which the C values are of course known exactly. The estimates of variance accounted for by the C factor in the simplexes of actual data in Tables 3.1 to 3.3 should reflect the upper limits of the heritabilities in the broadest sense, i.e., the proportion of total variance attributable to all genetic factors and in part to the covariance of genetic and environmental factors (see Equation A.6 in the Appendix on Heritability). One would expect a quite large covariance component in scholastic achievement, and would expect it to increase over the course of schooling. The squared first principal components would yield inflated estimates of broad heritability to the extent that the C factor also includes non-genetic constitutional factors and any constant environmental effects over the course of development.

Intelligence thus can be thought of psychologically as that aspect of mental ability which consolidates learning and experience in an integrated, organized way, relating it to past learning and encoding it in ways that permit its retrieval in relevant new situations. The products of learning become an aspect of intelligence (or are correlated of intelligence) only when they are organized and retrievable, generalizable and transferable to new problem situations. This is why an adult with, say, only an eighth-grade education but with an IQ of 140 appears generally brighter and more capable at most things than a college graduate with an IQ of 110. It strikes many of those who have observed, taught, worked with, or employed both kinds of persons, that the advantage, in the long run, is usually with the person with the higher IQ rather than with the more education. Some of our social institutions unfortunately are set up so as to reward education more than intelligence. This will change, however, with increasing equality of educational opportunity. Then, not the amount of education, but the amount of consolidated achievement (i.e., intelligently usable and transferable knowledge and skills) will be the chief criteria for selection and promotion.

Material that is learned by rote association and repetition may appear as gains on an achievement test, but it does not necessarily become consolidated or integrated into the usable, transferable knowledge that we associate with intelligence. Unless it is constantly rehearsed, such knowledge acquired by rote quickly fades and is unretrievable. Anyone who has tried to improve his vocabulary by memorizing definitions of esoteric words appreciates this fact. Thus, no one has yet discovered any way of teaching intelligence to those who are not born with it. To teach intelligence might mean to point out more or less all the conceivable connections, generalizations, and possible transfer of every item of acquired information, and to elicit and reinforce the appropriate responses to these situations. This could involve teaching more than anyone could ever learn. Probably no one would live long enough ever to acquire even a mental age of six. The design of a computer that can ‘learn’ and ‘think’ both inductively and deductively is necessarily very different from that of the computer which merely records and sotres items of information that can later be elicited by specific cues in a pushbutton fashion.

One of the ways in which scholastic achievement tests differ from intelligence tests is that at any given point in time, the usual achievement test scores reflect a relatively larger G or gain component, intended to assess what had been taught in the recent past in a particular grade in school. Since various subjects of the curriculum are newly introduced at different grades, the G component of achievement tests constitutes a larger proportion in relation to S than is the case for intelligence tests. The G component is largely a function of environmental influences, interests, motivation, and the like, acting at any given time. Bloom (1964, pp. 113-19) has reviewed convincing evidence that G is more related to environmental factors, while C is genetically and constitutionally determined. (Professor Bloom, however, may not concur in this interpretation.) Thus, accelerated achievement gains brought about by an enriched and intensified instructional program generally ‘fade out’ in a few months to a year. Without a strong consolidation factor, accelerated gains are not maintained without constant rehearsal of the acquired knowledge or skills. Because variance in achievement test scores reflects a larger gain component at any given time than do intelligence tests, which are designed to reflect the consolidation factor, one should expect populations that differ on the average on intelligence measures to differ significantly less on achievement measures at any cross-section in time, and this has been found to be the case (Coleman et al., 1966; Jensen, 1971a). Consolidated achievement, however, provided it involves intellectual skills, should show about the same magnitude of population differences as are shown by intelligence tests.

An interesting difference between scholastic achievement scores and intelligence test scores (including vocabulary) is that the latter go on increasing steadily throughout the summer months while the children are not in school, while there is an actual loss in achievement test scores from the beginning to the end of the summer. Much of the most recently learned material prior to the summer vacation has not been sufficiently rehearsed to become consolidated. The loss is greatest for those school subjects that depend least upon general intelligence (i.e., the consolidation factor) and depend most upon sheer learning and memory, such as spelling, punctuation, grammar, and mechanical or computational arithmetic and number facts, as contrasted with reading comprehension and arithmetic concepts (Beggs & Hieronymus, 1968).

Gains in achievement (and intelligence test raw scores) are relatively greater early in learning than later, largely because it is easier to consolidate gains at the ‘simple’ end of the scale than at the more complex (‘difficult’) end of the scale of intellectual tasks. When students simultaneously begin a new course of study, the diligent but intellectually mediocre students can keep up or even excel for a time near the beginning of the course; but soon it becomes increasingly difficult to keep ahead as they progress further into the complexities of the subject matter. For the less intelligent students consolidation does not keep up with their gains to the same extent as for the brighter students. The growth of intelligence is not reflected mainly by an increase in the ability for simple learning through practice, but in the ability to consolidate and understand increasingly complex material. As Leona Tyler (1965, pp. 78-9) has put it: ‘The child with an IQ of 80 is handicapped all through school not because he is slow or inept at learning things which are within the capacity of all the children at his age level, but because he is never ready to grasp new and more complex ideas at the time when they are ordinarily presented to children of his age.’ Readiness in large part is the ability to consolidate the knowledge and skills gained through daily learning experiences.

According to our model, at any given point in time, a performance measure of achievement status (S) usually reflects more of the consolidated component (C) than of the gains component (G), and this is increasingly true over the course of development. Since C is largely genetic and stable and G is largely environmental and random, an inference from the model is that brighter siblings (and twins) should show higher correlations for achievement than duller siblings. (At any cross-section in time the recent [and random] gain component of the achievement test score would be a smaller proportion of total [consolidated] achievement for the brighter sibs and thus would not so attenuate the correlation between them. In other words, their phenotypic correlation would be closer to their genetic correlation.) This result is in fact what has been found. Burt (1943) divided sibling pairs into two groups: those above the median in IQ (i.e., 100 IQ) and those below the median. The correlation between siblings’ scholastic achievement test scores was 0.61 for the above-average sibs and only 0.47 for the below-average sibs.

Another inference from our model is that sibling correlations (based on tests given at the same age for both sibs) in measures of intelligence should be substantial and should increase with age, while year-to-year measures of gain should show much lower or even negligible correlations. The status measures, which increasingly reflect C, therefore, would also increasingly reflect the genetic factors which the sibs have in common, while the gains, which reflect motivation and specific learning and largely fortuitous environmental factors, should show little, if any, sib correlation. This inference, too, has been substantiated in part in a longitudinal study conducted at the Fels Research Institute (McCall, 1970). The level (status) of intelligence at any given age was found to show much higher heritability than the pattern of changes (gains) in intelligence from one time to another (an average interval of 9 months). Although there is an increase in sib correlations with age, it is not statistically significant. The model also predicts that parent-child correlations should be higher when they are based on measures of the parent as an adult than measures of the parent taken at the same age as those on the child. McCall’s (1970) study, which also included parent-child correlations of test scores obtained when both parent and child were between 3 and 12 years of age, showed significantly lower parent-child correlations than have been found in studies of parent-child correlations in which the parent was measured as an adult. (The one exception reported in the literature is Burt’s [1966, Table 4] parent-child IQ correlation of 0.49 when the parents were adults and of 0.56 when the parents’ childhood IQs were used.) McCall (1970, p. 647) concludes:

. . . although the general level of IQ appears to show heritability, the pattern of IQ change over age possesses far less heritability (if any at all). . . . Siblings (and parent-child pairs) share some environmental elements (for example, general atmosphere of intellectual encouragement) as well as genes in common. However, whatever the factors that determine IQ change over age, apparently they are not simply the general family intellectual climate available to each sibling. Rather, one might speculate that the salient variables are relatively more specific events and intellectual circumstances which quite possibly interact with age, personality, social, and motivational factors.

The simplex growth model also predicts that individuals with higher genetic intelligence (i.e., higher C values in the model) should show greater intra-individual variability in measured IQ over the course of development. This was actually found to be the case in the data of Honzik et al. (see Table 3.3). A recent analysis of these data showed that children with the greatest year-to-year fluctuations in IQ manifested also a general upward trend in IQ and had the higher mean IQ over the course of development (Honzik and Gedye, personal communication).

Cumulative Deficit

The concept of ‘cumulative deficit’ is fundamental in the assessment of majority-minority differences in educational progress. Cumulative deficit is actually a hypothetical concept intended to explain an observable phenomenon which can be called the ‘progressive achievement gap’, or PAG for short. When two groups show an increasing divergence between their mean scores on tests, there is potential evidence of a PAG. The notion of cumulative deficit attributes the increasing difference betwen the groups’ means to the cumulative effects of scholastic learning such that deficiencies at earlier stages make for greater deficiencies at later stages. … There may be other reasons as well for the PAG, such as differential rates of mental maturation, the changing factorial composition of scholastic tasks such that somewhat different mental abilities are called for at different ages, disillusionment and waning motivation for school work, and so on. [...]

When the achievement gap is measured in raw score units or in grade scale or age scale units, it is called abolute. For example, we read in the Coleman Report (1966, p. 273) that in the metropolitan areas of the Northwest region of the U.S. ‘. . . the lag of Negro scores [in Verbal Ability] in terms of years behind grade level is progressively greater. At grade 6, the average Negro is approximately 1 ½ years behind the average white. At grade 9, he is approximately 2 ¼ years behind that of the average white. At grade 12, he is approximately 3¼ years behind the average white.’

When the achievement difference between groups is expressed in standard deviation units, it is called relative. That is to say, the difference is relative to the variation within the criterion group. The Coleman Report, referring to the findings quoted above, goes on to state: ‘A similar result holds for Negroes in all regions, despite the constant difference in number of standard deviations.’ Although the absolute white-Negro difference increases with grade in school, the relative difference does not. The Coleman Report states: ‘Thus in one sense it is meaningful to say the Negroes in the metropolitan Northeast are the same distance below the whites at these three grades – that is, relative to the dispersion of whites themselves.’ The Report illustrates this in pointing out that at grade 6 about 15 percent of whites are one standard deviation, or 1 ½ years, behind the white average; at grade 12, 15 percent of the whites are one standard deviation, or 3 ¼ year, behind of the white average.

It is of course the absolute progressive achievement gap which is observed by teachers and parents, and it becomes increasingly obvious at each higher grade level. But statistically a more informative basis for comparing the achievement differences between various subgroups of the school population is in terms of the relative difference, that is, in standard deviation units, called sigma (σ) units for short.

Except in the Southern regions of the U.S., the Coleman study found a more or less constant difference in approximately 1σ (based on whites in the metropolitan Northeast) between whites and Negroes in Verbal Ability, Reading Comprehension, and Maths Achievement. In other words, there was no progressive achievement gap in regions outside the South. In the Southern regions, there is evidence for a PAG from grade 6 to 12 when the sigma units is based on the metropolitan Northeast. For example, in the non-metropolitan South, the mean Negro-white differences (Verbal Ability) in sigma units are 1.5, 1.7, and 1.9 for grades 6, 9, and 12, respectively. The corresponding number of grade levels that the Southern Negroes lag behind at grades 6, 9, and 12 are 2.5, 3.9, and 5.2 (Coleman et al., 1996, p. 274). The causes of this progressive achievement gap in the South are not definitely known. Contributing factors could be an actual cumulative deficit in educational rates of the mental abilities relevant to school learning, and selective migration of families of abler students out of the rural South, causing an inreasing cumulation of poor students in the higher grades.

Selective migration, student turnover related to adult employment trends, and other factors contributing to changes in the characteristics of the school population, may produce a spurious PAG when this is measured by comparisons between grade levels at a single cross-section in time. The Coleman Report’s grade comparisons are cross-sectional. But where there is no reason to suspect systematic regional population changes, cross-sectional data should yield approximately the same picture as longitudinal data, which are obtained by repeated testing of the same children at different grades. Longitudinal data provide the least questionable basis for measuring the PAG. Cross-sectional achievement data can be made less questionable if there are also socioeconomic ratings on the groups being compared. The lack of any grade-to-grade decrement on the socioeconomic index adds weight to the conclusion that the PAG is not an artifact of the population’s characteristics differing across grade levels.

Another way of looking at the PAG is in terms of the percentage of variance in individual achievement scores accounted for by the mean achievement level of schools or districts. If there is an achievement decrement for, say, a minority group across grade levels, and if the decrement is a result of school influences, then we should expect an increasing correlation between individual students’ achievement scores and the school averages. In the data of the Coleman Report, this correlation (expressed as the percentage of variance in individual scores accounted for by the school average) for ‘verbal achievement’ does not change appreciably from the beginning of the first school year up to the twelfth grade. The school average for verbal achievement is as highly correlated with individual verbal achievement at the beginning of grade 1 as at grade 12. If the schools themselves contributed to the deficit, one should expect an increasing percentage of the total individual variance to be accounted for by the school average with increasing grade level. But no evidence was found that this state of affairs exists. The percent of total variance in individual verbal achievement accounted for by the mean score of the school, at grades 12 and 1, is as follows (Coleman et al., 1966, p. 296):

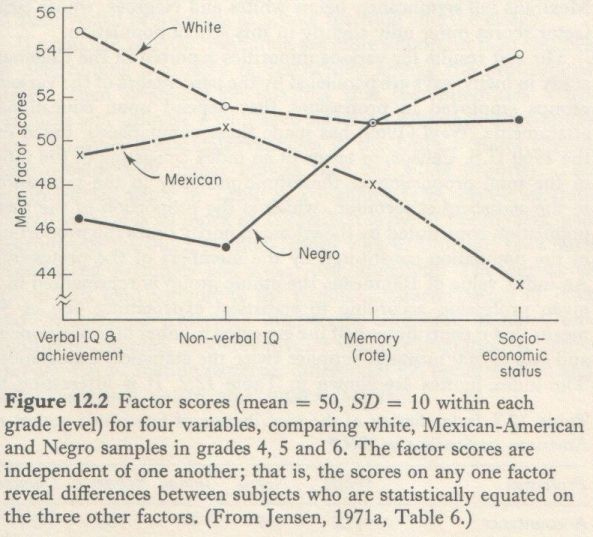
Jensen (1971a) also failed to find any evidence of increasing sigma differences between whites, Negroes, and Mexicans in scholastic achievement over grades 1 to 8 in cross-sectional testing in a California school district.

Longitudinal studies outside the South show the same thing. Harris and Lovinger (1968) obtained a variety of intelligence and achievement test scores on the same disadvantaged Negro and Puerto Rican (in the ratio 9 to 1) children in grade 1, 3, 6, 7, 8, and 9. The school attended by these children had the lowest average achievement of any junior high school in the borough of Queens, New York. There was no evidence of declining IQs in this group. Eighth and ninth grade IQs were approximately equal to first grade IQs. Another longitudinal study by Rosenfeld and Hilton (1971) compared the academic growth of Negro and white students who attended the same high schools and were enrolled in the same curricula. Ability tests were obtained in grade 5, 7, 9, and 11. In absolute level of achievement the Negro students were one to two years behind the white students on most of the tests, and the absolute gap increased over time. But the relative gap, in sigma units, did not increase. The gap was no greater in the eleventh grade than would be predicted on the basis of the fifth grade differences in mean scores between the groups. When equated for initial differences in test scores, Negroes and whites gained academically at substantially the same rates between grades 9 and 11 on tests of Reading, Writing, Social Studies, and Listening. Whites, however, grew at a faster rate in Maths and Science achievement and in tests of verbal and quantitative reasoning. In analyzing the test results on students enrolled in academic and non-academic curricula, Rosenfeld and Hilton found no significant interaction between curriculum and race: that is, the overall academic growth of the Negro students relative to the white did not depend on which curriculum they were enrolled in. The authors note:

Generally, the Negro students in the academic programs have test scores similar to the white students in the nonacademic programs. And generally, the Negro students in the academic programs have SES (socioeconomic status) scores similar to the white students in the nonacademic programs. Overall, the white nonacademics are more like the Negro academics in SES than they are like the white academics.

The one longitudinal study conducted in the South (Georgia) showed no overall decline in mean IQ from grade 6 to 10 for either Negro or white students, who differed by a constant amount of approximately 20 IQ points (Osborne, 1960). The scholastic achievement scores show the usual divergence of white and Negro means from grade 6 to 12, but we cannot tell from Osborne’s presentation of his results in terms of grade placement scores whether there is an increasing relative achievement gap in sigma units. Inspection of Osborne’s graphs suggests that there is little, if any, increase in the relative achievement gap between Negroes and whites from grades 6 to 12.

The absence of a relative progressive achievement gap (PAG) as measured in sigma units between racial or socioeconomic groups means that the absolute PAG is not a matter of race or SES per se but a matter of differences in intellectual growth rates. It means that (a) the educational process is not treating children of the two races differently and (b) Negro and white children per se are not responding differently to the educational treatment. They are responding according to their individual intelligence levels, and not according to their racial membership. The absence of a relative PAG means, for example, that a Negro and a white child matched for IQ and other abilities will have the same growth curves for scholastic achievement. The Negro child, in other words, does not do worse in school than his white counterpart in IQ, and this is true when the matching on IQ is done at the very beginning of the child’s schooling, before the schools can have had any cumulative effect on the child’s IQ performance. In one study, large representative samples of Negro and Mexican-American children from kindergarten through the eight grade in largely de facto segregated schools were compared with white children in the same California school district on a comprehensive battery of tests of mental abilities and of scholastic achievement, in addition to personality inventories and indices of socioeconomic and cultural disadvantage. It was found that when certain ability and background factors over which the schools have little or no influence are statistically controlled, there are no appreciable differences between the scholastic achievements (as measured by the Stanford Achievement Tests) of minority and majority pupils. And there is no evidence of a PAG between all majority and all minority pupils (who average about 1σ lower) when the differences are measured in sigma units (Jensen, 1971a).

Chapter 4

The Heritability of Scholastic Achievement

FAMILY INFLUENCES ON SCHOLASTIC ACHIEVEMENT

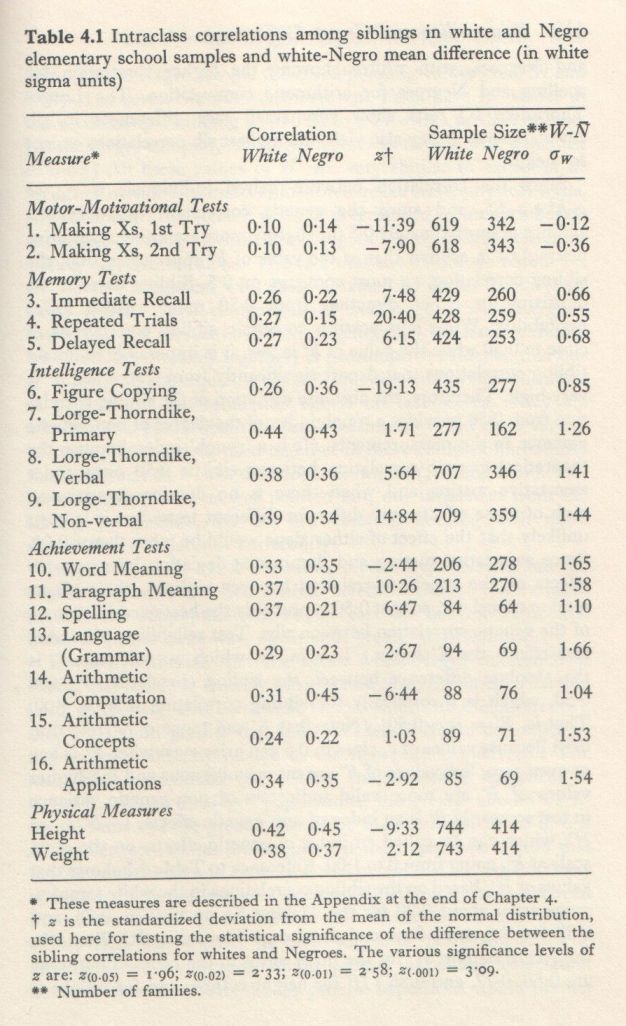
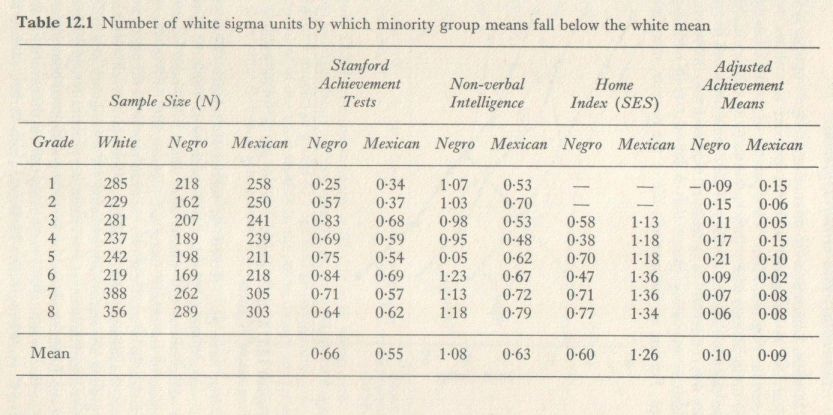
Table 4.1 shows the intraclass correlations of siblings in the white and Negro samples, the sample sizes for each test, and the value for determining the statistical significant of the difference between the r_i‘s of the two racial groups. We see that even though all but two of the tests show statistically significant differences between the sibling correlations for whites and Negroes, the actual magnitudes of the differences are generally quite small. The differences for the Lorge-Thorndike intelligence tests are of about the same magnitude as for height and weight. Sibling correlations for height provide a good reference point, since the heritability of height is very high and the genetic correlation between siblings for this trait is at least 0.50 or slightly more. If one racial group or the other had in it a larger proportion of half-siblings misidentified as full siblings, it would show up in the correlation; the group with more half-siblings would have the lower correlation, since half-sibs have a genetic correlation of only 0.25. Half-sibs who were identified as such were, of course, not included in this analysis. They were many more half-sibs excluded in the Negro sample. The fact that the Negro sibling correlation for height is even slightly higher than for whites suggests that the other Negro sib correlations are not likely to be attenuated by the presence of misidentified half-sibs in the sample. The same thing holds true for weight, although to a slightly less degree, since the heritability of weight is not quite as high as for height. In other studies, the heritability of weight has been found to be very close to that for intelligence, and our sibling correlations are consistent with this. The intelligence test sibling correlations are consistent with this. The intelligence test sibling correlations average just about the same as those for weight. The overall impression to be gained from Table 4.1, then, is that there is no marked difference between the white and Negro samples in the degree of family environmental influence on most tests. [5] The largest differences are found for a memory test which involves repeated trials, i.e., each digit series is repeated three times, instead of only once, prior to recall by the subject. Figure copying (the child copies 10 geometric forms of increasing complexity) shows a considerably higher sib correlation for Negroes (0.36 v. 0.26 for whites). Of the scholastic achievement tests, spelling and arithmetic computation show the largest sib correlation differences between whites and Negroes, with whites showing the higher correlation for spelling and Negroes for arithmetic computation. The Lorge-Thorndike IQ tests show very small race differences in sib correlations and they also yield the highest sib correlations except for height.

Since the correlation between paired individuals is r_AB = p_Gh²+p_EE², and since the genetic correlation (p_G) between siblings is approximately 0.5 (or slightly more assuming assortative mating), it is evident that as the value of h² approaches 1.00, the sibling correlation, r_s, must converge on 0.5. Sibling correlations departing in either direction from 0.50 must involve lower heritability. While it is possible to obtain sibling correlations of close to 0.50 when the value of h² is low, it is impossible to obtain sibling correlations that depart significantly from 0.50 when h² is very high. Therefore, the absolute deviation of the sibling correlation from 0.50 provides a rough index of the degree of non-genetic variance in the measurements. (It is a ‘rough’ index because the theoretical genetic correlation between sibs is 0.50 only under assortative mating and when there is no dominance variance; each of these effects may differ for different tests, but it is most unlikely that the effect of either alone would be more than ±0.05. Since assortative mating and dominance deviation have opposite effects on the genetic correlation between siblings, their effects tend to cancel out, so that 0.50 is probably the best overall estimate of the genetic correlation between sibs. Test reliability, of course, also effects the E’ index.) This index, which we will call E’, is the absolute difference between the sibling correlation, r_s, and 0.50, which is theoretically the sibling correlation if h² = 1.00.

That is, E’ = |r_s-0.50|. (Note that E’ can range only from 0 to 0.50.) Because values or r_s close to 0.50 can arise even when h² is low or even zero, low values of E’ are more ambiguous and the higher values of E’ are more valid indicators of non-genetic variance in test scores. If E’ is an index of non-genetic effects, 1-E’/p_G = H’, which can be called an index of genetic effects, no the same scale as h², going from 0 to 1.00. Reference to Table 4.1 shows that values of H’, based on the sibling correlations in the white samples, range from about 0.20 for the Making Xs up to 0.76, 0.78, and 0.88 for the three forms of the Lorge-Thorndike IQ Test. (In the Negro sample, H’ for the three forms of the Lorge-Thorndike are 0.68, 0.72, and 0.86.) H’ for height is 0.84, and for weight is 0.76. (In the Negro sample the corresponding values are 0.89 and 0.74). The seven Stanford Achievement Tests have H’ values in the white sample ranging from 0.48 to 0.74 with a median of 0.66. (In the Negro samples, H’ ranges from 0.42 to 0.90 with a median of 0.60.) All these values of H’ are very similar to values of h² (or other heritability indices) for intelligence tests, physical traits, and scholastic achievement when h² is estimated by more elaborate and moer accurate means than is possible by estimation from sibling correlations alone. The fact that the values we obtain for H’ are very consistent with those obtained by better means (e.g., twins reared apart, comparison of monozygotic and dizygotic twins, and the correlation between genetically unrelated children who have been reared together) is presumptive evidence that our H’ index, and consequently also E’, are reasonably valid indicators of genetic and environmental effects on test scores. They are admittedly a poor substitute for h² estimates based on a variety of kinship correlations used together in more complex heritability formulas such as I have described elsewhere (Jensen, 1967). Yet, in the present data, as was pointed out, our inferences from the sibling correlations, via E’, are quite in keeping with more dependable estimates of heritability.

Just as we could use h² in testing certain hypotheses about the degree of genetic and non-genetic determination of test variance in different subpopulations, so we can our environmental index E’ in the same way, albeit with greater reservations.

If we hypothesize that the mean white-Negro difference in ability test scores is entirely attributable to environmental factors (and, conversely, that no genetic factors enter into the difference), then we should predict that the mean white-Negro difference in test scores is directly related to the non-genetic index, E’. The more that a particular test reflects environmental influences in either the white or Negro populations, the greater should be E’ for that test and the greater should be the mean difference in test scores between whites and Negroes if the hypothesis is true that the mean difference is entirely environmental. One possible way of testing this hypothesis is would be to obtain the correlation between the mean white-Negro difference (W̅-N̅) and E’ on a variety of ability tests which differ in their values of W̅-N̅ and E’. The environmental hypothesis would predict a positive correlation between those variables. A genetic hypothesis would predict a negative correlation. Often genetic and environmental hypotheses of subpopulation differences lead to the same predictions so that one cannot decide between them on the basis of empirical outcomes. But here we have a situation in which environmental and genetic hypotheses predict diametrically opposite outcomes.

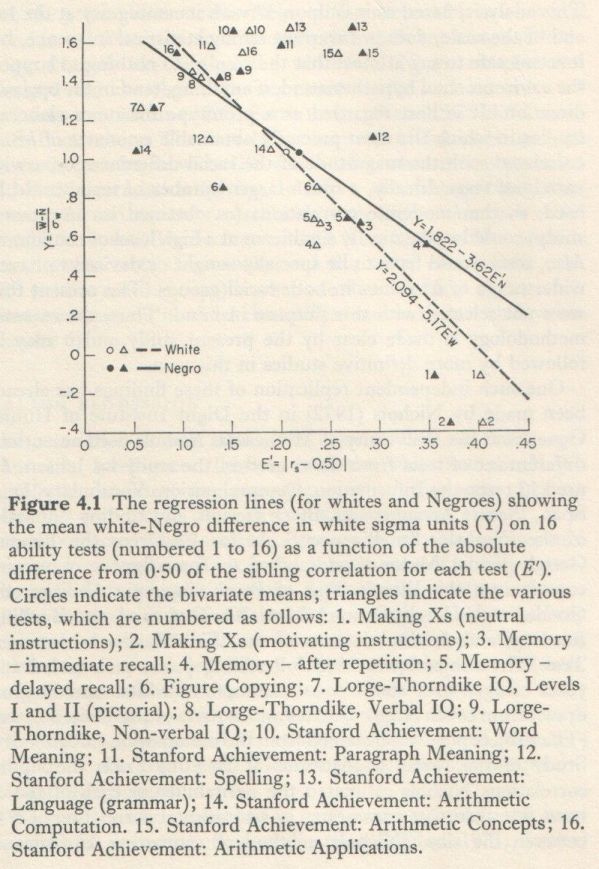
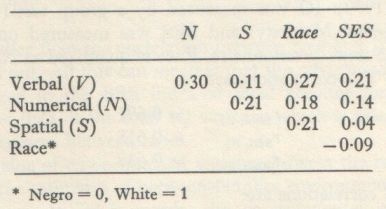
Using the data of Table 4.1 (omitting height and weight), we can determine the correlation between E’ and W̅-N̅/σ_W. The mean white-Negro difference must be divided by the standard deviation in the white sample (σ_W) in order to express all the differences on the same scale for the various tests. The differences are thus expressed in white sigma units.[6] Figure 4.1 shows the scatter diagram relating W̅-N̅/σ_W (the Y axis) and E’ = |r_s-0.50| (the X axis). The white samples are plotted as white triangles and the Negro samlpes as black triangles. The two bivariate means are indicated by white and black circles. The regression lines for the regression of Y on X are shown for both the white and Negro groups. The regression line for whites has a somewhat steeper slope than for Negroes. But in both cases the slope is negative, which is oppositve to the prediction from the environmental hypothesis. The Pearson r between W̅-N̅/σ_W and E’ = |r_s-0.50| is -0.80 for whites and -0.61 for Negroes. The correlation between the Negro and white values of E’ is 0.71. This r of 0.71 means that the various tests are quite similar for whites and Negroes in the degree to which they reflect non-genetic factors. (Since the reliabilities of all these tests are quite uniformly high and about the same for Negroes and whites, corrections for attenuation would have a negligible effect on the results.)

Since extreme values on either the X or Y axis can inflate the Pearson r, it is desirable to obtain a measure of correlation which is free of the effects of scale and cannot be spuriously inflated by extreme values. Spearman’s rank order correlation (rho) provides this measure. For whites rho is -0.56 and for Negroes rho is -0.47. The rho between white and Negro E’ values is 0.64.

The most extreme values on both X and Y variables are those of tests #1 and #2, the Making Xs Test, which is not a cognitive test but a motor skills test and was intended largely to reflect test-taking motivation and effort. It is known to be sensitive to instructions and situational factors and so it is not surprising that it should show the highest E’ index. We should also determine the correlations when these two tests are eliminated, to make sure that all of the correlation is not caused by these two parts of a single test which does not measure mental ability to any appreciable degree. When tests #1 and #2 are eliminated, the Pearson r’s for whites and Negroes are -0.44 and -0.34, respectively. The r between Negro and white E’ values is 0.54. The rank order correlations (rho) after tests #1 and #2 are eliminated are -0.34 for whites and -0.20 for Negroes. The rho between white and Negro E’ values is 0.46. Thus when the two non-cognitive tests are left out and rank order correlation is used, the correlations are unimpressive. The most impressive aspect is that they are negative, while the environmental hypothesis predicts positive correlations.

This analysis, based as it is upon E’ with its ambiguity at the low end of the scale, does not warrant strong statistical inference, but it seems safe to say at most that the results do nothing to support the environmental hypothesis and, if anything, tend in the opposite direction. It is best regarded as a prototype for more elaborate studies in which the most precisely obtainable estimates of h² are correlated with the magnitude of the racial differences on a wide variety of tests. Ideally, a much larger number of tests would be used, so that moderate correlations (as obtained in the present study) could be statistically significant at a high level of confidence. Also, tests would have to be specially sought or devised to have a wider range of h² values in both racial groups. The present tests were not selected with this purpose in mind. Thus, the essential methodology is made clear by the present study and it may be followed by more definitive studies in this vein.

Nichols then obtained the correlation of the heritabilities of each of the 13 tests with the magnitudes of the average difference (in standardized units) between whites and Negroes on each of the tests. This correlation was +0.67. That is, the higher the heritability of the test, the greater is the white-Negro difference … . Nichols also pooled the white and Negro samples and obtained the correlation between test scores and an index of socioeconomic status (SES). Some tests reflected SES differences more than others. The correlation between h² for each test and the test’s correlation with SES was +0.86; when race is partialed out of this correlation (giving, in effect, the average correlation between h² and the tests’ correlation with SES within each racial group), the correlation becomes +0.74. This high positive correlation between tests’ heritability and the tests’ correlations with SES (within racial groups) is what one should expect if there is a genetic component in social class differences in mental ability … .

SIBLING REGRESSION

The correlation among siblings of close to 0.40 on the Lorge-Thorndike Intelligence Tests in both the white and the Negro samples has an interesting consequence which may seem puzzling from the standpoint of a strictly environmental theory. It is entirely expected if one assumes a genetic model of intragroup and intergroup differences. This is the phenomenon of sibling regression toward the population mean. If one picks children who are tall for their age, it is found that their siblings are about halfway between the tall children and the mean of the population from which they were sampled. Conversely, if one picks short children, their siblings will be taller – about halfway between the short children and the population mean. The same is true for numbers of fingerprint ridges and all other polygenically inherited characteristics. It is also true of IQ. Genetic theory predicts the precise amount of regression.

We have clearly established in our research (and it has been corroborated in many other studies [see Stanley, 1971; Sattler, 1972]) that if we match Negro and white children for IQ, their performance on scholastic achievement tests is so equivalent as not to differ statistically even with very large sample sizes. In other words, the IQ test gives the same prediction of scholastic performance for Negro children as for white children.

But if we match a number of Negro and white children for IQ [7] and then look at the IQs of their full siblings with whom they were reared, we find something quite different: the Negro siblings average some 7 to 10 points lower than the white siblings. Also, the higher we go on the IQ scale for selecting the Negro and white children to be matched, the greater is the absolute amount of regression shown by the IQs of the siblings. [8] For example, if we match Negro and white children with IQs of 120, the Negro siblings will average close to 100, the white siblings close to 110. The siblings of both groups have regressed approximately halfway to their respective population means and not to the mean of the combined populations. The same thing is found, of course, if we match children from the lower end of the IQ scale. Negro and white children matched for, say, IQ 70 will have siblings whose average IQs are about 78 for the Negroes and 85 for the whites. In each case the amount of regression is consistent with the genetic prediction. The regression line, we find, shows no significant departure from linearity throughout the range from IQ 50 to 150. This very regular phenomenon seems difficult to reconcile with any strictly environmental theory of the causation of individual differences in IQ that has yet been proposed. If Negro and white children are matched for IQs of, say, 120, it must be presumed that both sets of children had environments that were good enough to stimulate or permit IQs this high to develop. Since there is no reason to believe that the environments of these children’s siblings differ on the average markedly from their own, why should one group of siblings come out much lower in IQ than the other? Genetically identical twins who have been reared from infancy in different families do not differ in IQ by nearly so much as siblings reared together in the same family. It can be claimed that though the white and Negro children are matched for IQ 120, they actually have different environments, with the Negro child, on the average, having the less intellectually stimulating environment. Therefore, it could be argued he actually has a higher genetic potential for intelligence than the environmentally favored white child with the same IQ. But if this were the case, why should not the Negro child’s siblings also have somewhat superior genetic potential? They have the same parents, and their degree of genetic resemblance, indicated by the theoretical genetic correlation among siblings, is presumably the same for Negroes and whites. [9]

NOTES

[6] Another possible way of expressing the racial difference on a common scale for all tests would be by the point-biserial correlation (r_pbs) between test scores and the racial dichotomy (quantized as 0 and 1). But r_pbs bears a non-linear relationship to (W̅–N̅)/σ_W and when used as an index to be correlated with another variable coul result in a non-linear but monotonic relationship to the other variable which would underestimate the degree of relationship if the Pearson r were used. In such a case, either the correlation ratio (eta) or Spearman’s rank order correlation (rho) should be used as the measure of degree of relationship instead of the product-moment correlation (Pearson’s r).

[7] Technically speaking, the Negro and white children are matched on ‘regressed true scores’ (regressed to the common mean), that is, the IQ scores they would be expected to obtain if errors of measurement were eliminated. This is a standard statistical procedure generally called for in studies based on the matching of individuals from two or more groups.

[9] Actually, the genetic sibling correlation would be slightly higher in whichever group had the highest degree of assortative mating (i.e., correlation between spouses) for IQ. At present there is no good evidence concerning the degree of assortative mating for IQ in the Negro population, although one study found no Negro-white difference in degree of assortative mating for amount of formal education. (Warren, 1966)

Chapter 6

Social Class Differences in Intelligence

… Since we know that the largest part of the IQ difference between siblings is due to genetic factors, it follows that social mobility must lead to some segregation of the gene pool for abilities. This has been shown most strikingly in a recent study by Waller (1971b), who found that the greater the difference in IQ test score between father and son (both tested at high school age), the greater is the probability that the son will be socially mobile, for both upward and downward social mobility. The correlation between father-son IQ difference and father-son difference on a composite index of SES is +0.29 ± 0.08. When the two most extreme classes (I and V) of fathers were excluded, the correlation based on classes II, III, and IV is +0.37 ± 0.07. The correlation between high school IQ and adult SES is +0.69 for the fathers and +0.57 for the sons. It has been noted in several studies that this correlation increases gradually with age, as persons approach their own highest levels of occupational attainment. [...]

The statistical argument goes as follows: The correlation between phenotypes (the measurable characteristic) and genotypes (the genetic basis of the phenotype) is the square root of the heritability, or h. An average estimate of h for intelligence in European and North American Caucasian populations is 0.90. An estimate of the average correlation between occupational status and IQ is 0.50. A purely environmentalist position says that the correlation between IQ and occupation (or SES) is due entirely to the environmental component of IQ variance. In other words, this hypothesis requires that the correlation between genotypes and SES be zero. So we have correlations between these sets of variables: (a) between phenotype and genotype, r_pg = 0.90; (b) between phenotype and status, r_ps = 0.50; and (c) the hypothesized correlation between genotype and status, r_gs = 0. The first two correlations (r_pg and r_ps) are determined empirically and are here represented by the average values reported in the literature. The third correlation (r_gs) is hypothesized to be zero by those who believe genetic factors may play a part in individual differences but not in SES group differences. The question then becomes: is this set of correlations possible? The first two correlations we know are possible because they are empirically obtained values. The only correlation seriously in question is the hypothesized r_gs =0. Now we know that mathematically the true correlations among a set of three variables, 1, 2, 3, must meet the following requirement: [2]

r²₁₂+r²₁₃+r²₂₃ -2r₁₂r₁₃r₂₃ <1

The fact is that when the values of r_pg = 0.90, r_ps = 0.50 and r_gs =0 are inserted into the above formula, its yields a value greater than 1.00. This means that r_gs must in fact be greater than zero.

Another, more intuitive way of stating this problem is as follows: if only the environmental component (i.e., 1–h²) determined IQ differences between status groups, then the h² component of IQs would be regarded as random variation with respect to SES. Thus, in correlating IQ with SES, the IQ test in effect would be like a test with a reliability of 1–0.80 = 0.20. Therefore, the theoretical maximum correlation of IQ with SES would be close to SQRT(0.20) = 0.45. This value is slightly below but still very close to the average value of obtained correlations between IQ and SES. So if we admit no genetic component in SES IQ differences, we are logically forced to conclude that persons have been fitted to their SES (meaning largely educational and occupational attainments) almost perfectly according to their environmental advantages and disadvantages. In other words, it would have to be concluded that persons’ innate abilities, talents, and proclivities play no part in educational and occupational selection and placement. This seems a most untenable conclusion. The only way we can logically reject the alternative conclusion – that there are average genetic intelligence differences among SES groups – is to reject the evidence on the heritability of individual differences in intelligence.

Chapter 7

Race Differences in Intelligence

TWIN DIFFERENCES AND RACE DIFFERENCES

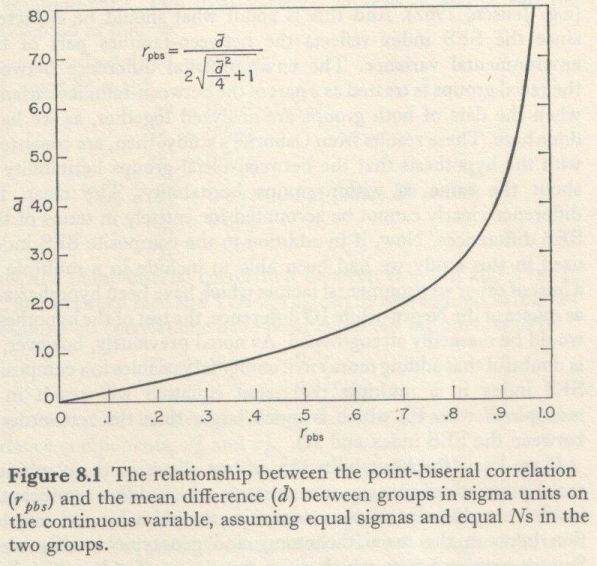
The analysis shows that the mean absolute difference in IQ between twins for the data of all studies combined is 6.60, SD = 5.20. The mean differences range from 5.96 to 8.21 in the various studies – differences which are not statistically significant, so that 6.60 is the best available estimate of the mean IQ difference between MZ twins reared apart. But we cannot compare this value directly with any mean difference between racial groups, because the mean absolute difference between twins includes the test’s measurement error, while the difference between the means of two groups does not include measurement error. Therefore, to make the mean absolute difference between twins comparable to the mean difference between, say, Negroes and whites, we must either remove the measurement error from the twin differences or include it in the racial mean difference. It is more logical to do the former. If the reliability of the IQ tests is assumed to be 0.95 (the upper bound of reliability of the Stanford-Binet) and we correct the mean difference of 6.60 for attenuation by removing measurement error, the ‘true-score’ absolute difference between the MZ twins is 5.36 IQ points. [3] This, then, is the twin difference which should be compared with the mean Negro-white difference of 15 IQ points. But we should go further and look at the entire distribution of the true-score differences between the members of each MZ twin pair. A so-called ‘regressed true score’ is the statistically best estimate of an individual’s ‘true’ score on a test, i.e., the estimated score he would have obtained if the test scores were free of measurement error. [4] Figure 7.1 shows the distribution of true-score differences for the 122 MZ twin pairs. [5] It should be noted that of the total of 122 pairs of MZ twins reared apart, only six pairs (5 percent) show true-score differences greater than the mean Negro-white difference of 15 IQ points and only three pairs (2.5 percent) show true-score differences greater than 16 points (18, 20, and 22).

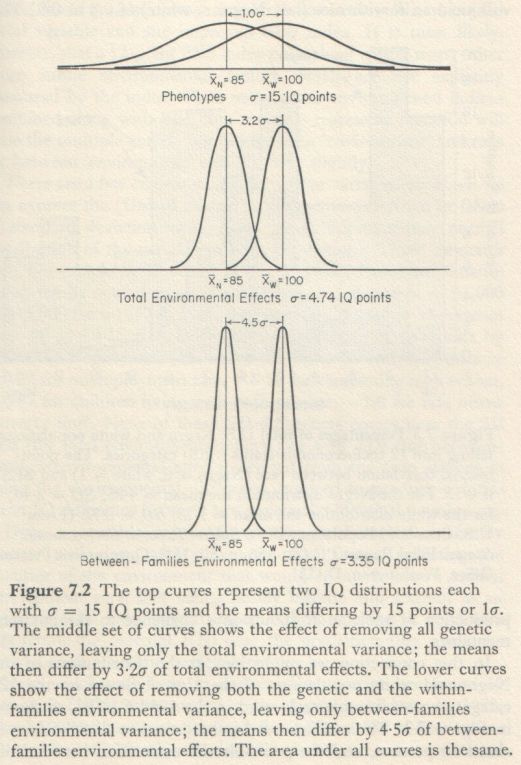
The distribution of twin differencs in IQ, it turns out, does not differ significantly from the theoretical χ (chi) distribution. This is convenient, since the χ distribution is, in a sense, one-half of a normal distribution. If we were to graph a frequency distribution of the absolute differences between a very large number of randomly paired values each selected at random from a normal (Gaussian) distribution, the result would approximate a χ distribution. Now, since the only difference between the MZ twin pairs is due to non-genetic or environmental factors, and since the twin differences in IQ closely approximate a χ distribution, we can conclude that the effects of environment on IQ have a normal distribution in this twin sample. Moreover, it is possible to determine the standard deviation (SD) of the distribution of the effects of environmental differences on IQ. The SD is 4.74 IQ points. [6]

Since in a normal distribution six sigmas encompass virtually 100 percent of the population (actually all but 0.27 percent), and since the SD of environmental effects on IQ in the total twin sample is 4.74, it can be said that the total range of environmental effects in a population typified by this twin sampl is 6 x 4.74 = 28.4 IQ points. This value is referred to by geneticists as the reaction range of IQ under natural conditions. This determination of the reaction range is slightly greater than the values conjectured by Gottesman (1968, p. 34) of 24 points, by Bloom (1964, p. 71) of 20 points, and by Cronbach (1969, p. 343) of ‘more than 25 points’.

Thus, we now have a scale of the effects of environments (in population similar to the twin samples), with one SD on the scale being equivalent to 4.74±0.3 IQ points. That is to say, two genetically identical individuals who differ by 4.74 IQ points (true-score values) can be said to differ by one SD on the scale of the effects of environment on IQ. [7]

If, then, we hypothesize that the mean difference of 15 IQ points between Negroes and whites is due entirely to non-genetic causes, we must conclude that the two populations differ by 15/4.74 = 3.2 SDs on our environmental scale. With a difference this large, only 0.07 percent of the lower group exceeds the median of the higher group.

But here we are considering the total non-genetic or environmental effects in the twin samples. The total environmental variance can be analyzed into two parts: (a) variance due to environmental effects (i.e., differences) between families, and (b) variance due to environmental effects within families, including unequal prenatal effects on each member of a twin pair. (These environmental differences operating within families and making for environmental differences among children reared together are sometimes referred to as micro-environmental effects.) The proportions of variance attributable to the between and within components are estimated from the difference between MZ twins reared together in the same family (MZT) and MZ twins reared apart in different families (MZA). The differences between the mean absolute difference among MZA and MZT give an estimate of the within-families and between-families effects. The differences between MZ twins reared apart is attributable to both the within-families and between-families environmental effects; the difference between MZ twins reared together is attributable only to the within-family effects. Subtracting the difference for MZT from the difference for MZA, therefore, gives us the difference attributable to between-family effects. When this is done on MZT and MZA data where both types of twins are from comparable populations, the within-families environmental effect usually turns out to be slightly larger than the between-families effect on IQ (Jensen, 1970a, p. 145). But to keep the argument simple, let us assume that the between and within variances are approximately equal. This would mean that half the within-MZA twin variance is due to environmental differences between families. Since the variance of total (i.e., between and within) environmental effects on IQ is (4.74)² or 22.5, the SD of the between-families environmental effects SQRT(22.5/2) = 3.35 IQ points. That is to say, a difference of one SD in the effects on IQ of differences among families’ environments is equivalent to 3.35 IQ points difference between genetically identical twins.

Environmental theories of Negro-white IQ differences usually assume that the causal environmental factors are predominantly those we normally classify as between-family differences, such as parental occupations, education, income maternal and child nutrition and health care, cultural advantages in the home, and the like. [...]

So, if one SD of between-families environmental difference corresponds to 3.35 IQ points in our twin population, the mean difference of 15 IQ points in our twin population, the mean difference to 15 IQ points between Negroes and whites is equivalent to 15/3.35 = 4.48 SDs on the between-families environmental scale. Two normal distributions with means more than 4 sigmas apart are almost totally non-overlapping. A strictly environmental hypothesis of the racial IQ differences based on existing twin data, therefore, leads to the conclusion that the distributions of total environmental effects on IQ are only slightly overlapping in the Negro and white populations and the between-families environmental effects are practically non-overlapping. … These data, therefore, strongly suggest that if the Negro-white IQ diference is attributable entirely to non-genetic factors, these must exist in some as yet unmeasured aspect of the environment, for no one has yet identified or measured any set of environmental conditions on which the Negro and white populations differ, on the average, by even half as much as 3 sigmas. [8] A multiple point-biserial correlation (R) between a host of environmental measures and the Negro-white dichotomy (treated as a quantized variable) would have to be approximately 0.8 for the sigma difference between the group means on the enviromental scale to be as great as 3 sigmas and R would have to be 0.9 for the mean environmental difference to be as great as 4.5 sigmas. Is there any known set of environmental variables which when optimally combined in a multiple regression equation will yield an R with race (i.e., Negro v. white) of 0.8 or 0.9? [...]

There are a few environmentally relevant variables on which we can express the (United States) Negro-white difference in terms of standard deviation units, assuming an approximately normal distribution of the variable in both populations. These estimates have been made by Shockley (1969, p. 1432). Based on statistics for all family annual incomes in the U.S. population from $3,000 to $15,000 from 1947 to 1966, the mean family income of Negroes was -0.80±0.15 SDs below that of whites. The SD units by which the Negro mean falls below the white on other variables is: -0.33 for unemployment rate, -0.52 for completing high school, -0.87 for children living with both parents, -1.0 for rate below ‘poverty line’. None of these SD differences comes near the 3.2 SDs (for total environmental effects) or 4.48 SDs (for between-families environmental effects) derived from the twin studies as being the environmental difference required to produce a 1 SD mean IQ difference between two genetically identical populations. [...]

By reckoning from the same model, the average Negro income gap of -0.80±0.15 would account for about 0.80 x 3.35 = 2.7 IQ points (or 18 percent) of the 15 IQ points difference between the racial IQ means. It must be concluded that income differences can account for only a small fraction (less than one-fifth) of the 15 points mean IQ gap between Negroes and whites.

A frequent criticism of basing estimates of environmental variance on the pooled data from studies of MZ twins reared apart is that the distribution of environmental differences in these samples is probably somewhat less than the total range of differences found in the general population. But since we have used the actual SD of twin samples in our analysis, we have taken the reduced variability into account, and this criticism therefore is not valid. The valid conclusion is that … it is highly improbable that the mean Negro-white difference can be explained by such environmental effects. The Negro and white populations of the United States would have to be assumed to differ by 3 to 5 sigmas on the scale of environmental effects [...]

It seems more sensible, however, to base our environmental scale on broader estimates of heritability than just those derived from MZ twins reared apart. Such an estimate can be obtained by using all he kinship correlations reported in the literature, including all twin data. When this was done, an overall h² of 0.77 (or 0.81 when corrected for attenuation) was obtained (Jensen, 1969a, p. 51). If we use h² = 0.80, the distribution of environmental effects on true-score IQs (assuming test reliability = 0.95) will have a standard deviation of SQRT(1-0.80{(0.95)(15)²}) = 6.5 IQ points, and the total reaction range of environmental effects (from the ‘worst’ environment in a thousand to the ‘best’ in a thousand) would be 6 x 6.5 = 39 IQ points. Using the environmental SD = 6.5, a mean difference of 15 points between Negroes and whites, explained environmentally, would therefore require a difference of 2.3 SDs on this environmental scale. The SD of between-families environmental effects would be about 4.6 IQ points, and on this scale the Negro and white populations would have to differ by 3.3 SDs if we wish to entertain the hypothesis that all of the 15 IQ points difference is due to differences between family environments. Thus, even using a larger environmental component than that estimated from MZ twins reared apart, the differences between Negro and white means required by the environmental hypothesis are still much larger than any actual environmental differences reported between Negro and white populations. [11]

GENOTYPE X ENVIRONMENT INTERACTION

The genotype x environment (G x E) interaction often figures prominently in discussions of the genetics of race differences in intelligence (e.g., Gottesman, 1968, pp. 30-2; Bodmer & Cavalli-Sforza, 1970, p. 29). The G x E interaction means either one, or both, of two things: (a) that what constitutes a good environment for one genotype may constitute a bad environment for some other genotype in terms of the development of the phenotype; and (b) that environmental advantages (or disadvantages), though acting in the same phenotypic direction for all genotypes, may have unequal phenotypic effects on different genotypes. For example, a good environment may result in great phenotypic similarity for genotypes A and B, while a poor environment may lower A’s phenotype only slightly but may drastically push down B’s phenotype. The possibility of G x E interaction for a given trait thus holds out the hope that if only the optimal environment were found, or genotypes were optimally matched to different environmental conditions, the phenotypes could be equalized on the trait in question despite genotypic differences. All of the examples ever cited of such G x E interaction are taken from plant and animal breeding experiments and involve a relatively narrow characteristic. The favorite example is the experiment by Cooper and Zubek (1958), who, through selective breeding, established ‘dull’ and ‘bright’ strains of rats in maze learning ability and found that when both strains were raised under conditions of sensory deprivation they performed almost equally poorly in maze learning, and when both strains were raised in a sensorily ‘enriched’ environment they performed almost equally well; only when the groups were raised under normal laboratory conditions (the same as the selectively bred parental generations) did they show large differences in maze learning. In short, the magnitude of the phenotypic differences between the strains varied markedly under different environmental conditions – a perfect example of G x E interaction.

Such interaction with respect to human intelligence, and particularly genetic racial differences in intelligence, cannot be ruled out on the basis of present evidence. But it is seldom noted by those who emphasize G x E interaction that no evidence for it has been turned up in any of the studies of the heritability of human intelligence. It should show up in lower correlations between monozygotic (MZ) twins and between dizygotic (DZ) twins than those predicted from a simple additive model with assortative mating, and possibly with some dominance (which can be distinguished from G x E interaction by examining the parent-offspring correlations). The correlations obtained between DZ twins (also parent-child and sibling correlations) do not depart sufficiently from a genetic model without G x E interaction as to give much indication that any such interaction exists for human intelligence, at least in the Caucasian populations that have been sampled.

One of the conceptually neatest methods for detecting one kind of G x E interaction, first proposed by Jinks and Fulker (1970, pp. 314-15), is applicable to our data on MZ twins reared apart. We can ask: Are different genotypes for intelligence equally affected by environmental advantages (or disadvantages)? In the case of genetically identical twins, any phenotypic difference between them reflects some environmental difference. One twin can be said to be environmentally advantaged and the other disadvantaged, relative to one another. While the phenotypic difference between the twins, |t₁–t₂|, reflects only environmental effects, the average of their phenotypes, (t₁+t₂)/2, reflects their genotypic value (plus the average of their environmental deviations). If this correlation is significantly greater than zero, we can claim a G x E interaction. A positive correlation would mean that genotypes for high intelligence are more susceptible to the influence of good or poor environments; a negative correlation would mean that genotypes for lower intelligence are more sensitive to the effects of environment. The correlation of IQ differences with IQ averages of the 122 MZ pairs is -0.15, which is not significantly different from zero. When measurement error is removed by using regressed true scores instead of the obtained IQs, the correlation falls to -0.04. Thus the twin data reveal no G x E interaction. This finding is consistent with Jinks and Fulker’s (1970) failure to find any evidence for a G x E interaction in their analysis of a number of studies of the heritability of intelligence.

A THRESHOLD HYPOTHESIS OF ENVIRONMENTAL EFFECTS

… Although non-verbal tests are generally considered to be less culture-biased than verbal tests, it is the non-verbal tests which in fact show the greater discrepancy in his comparison, with the lower-status whites scoring higher than the upper-status Negroes. But in this comparison it is the upper-status Negro groups that has the higher heritability (i.e., greater genetic variance) on both the verbal and non-verbal tests. [...]

This finding is more difficult to reconcile with a strictly environmental explanation of the mean racial difference in test scores than with a genetic interpretation which invokes the well-established phenomenon toward the population mean. In another article Scarr-Salapatek (1971b) clearly explicated this relevant genetic prediction, as follows:

Regression effects can be predicted to differ for blacks and whites if the two races indeed have genetically different population means. If the population mean for blacks is 15 IQ points lower than that of whites, then the offspring of high-IQ black parents should show greater regression (toward a lower population mean) than the offspring of whites of equally high IQ. Similarly, the offspring of low-IQ black parents should show less regression than those of white parents of equally low IQ. (Scarr-Salapatek, 1971b, p. 1226)

In other words, on the average, an offspring genetically is closer to its population mean than are its parents, and by a fairly precise amount. Accordingly, it would be predicted that upper-status Negro children should, on the average, regress downward toward the Negro population mean IQ of about 85, while lower-status white children would regress upward toward the white population mean of about 100. In the downward and upward regression, the two groups’ mean could cross each other, the lower-status whites thereby being slightly above the upper-status Negroes. Scarr-Salapatek’s data (Table 3) are quite consistent with this prediction. Her finding is not a fluke; the same phenomenon has been found in other large-scale studies (see Chapter 4, pp. 117-19).

NOTES

3. The correlation between twins can be determined from the mean absolute difference |d̅_k| between twin pairs from the following formula

r = 1 (|d̅_k| / |d̅_p|)²

where

|d̅_k| = mean absolute difference between kinship members,
|d̅_p| = mean absolute difference between all possible paired comparisons in the general population, and

|d̅_p| = 2σ/SQRT(π) = 1.13σ

Since the population σ for IQ is 15, and the twin difference is 6.60, the above formula yields a value for r = 0.85. Thus, if the genetic variance for IQ = 0.85 x 15² = 191.25, and the error variance is (1-r_tt)σ² [where r_tt is test reliability] = (0.05)15² = 11.25, and the total variance is 15² = 225, then the environmental variance (i.e., the remainder) must equal 22.50, which has a standard deviation of SQRT(22.50) = 4.74. Assuming a normal distribution of environmental effects, the mean absolute difference in IQ due to environmental differences is 1.13 x 4.74 = 5.36.

7. In a classic study, Burks (1928) estimated the effects of environment on IQ from an analysis of correlations between detailed ratings of the home environment and the IQs of adopted children. A multiple correlation (corrected for attenuation) between the actual environmental ratings and IQ was 0.42 (The correlation between IQ and the theoretical environmental scale derived in our twin study is 0.32.) Burks concluded from her analyses of the IQs and environments of adopted children that

1. The total effect of environmental factors one standard deviation up or down the scale is only about 6 points, or, allowing for a maximal oscillation of the corrected multiple correlation (0.42) of as much as 0.20, the maximal effect almost certainly lies between 3 and 9 points. 2. Assuming the best possible environment to be three standard deviations above the mean of the population (which, if ‘environments’ are distributed approximately according to the normal law, would only occur about once in a thousand cases), the excess in such a situation of a child’s IQ over his inherited level would lie between 9 and 27 points – or less if the relation of culture to IQ is curvilinear on the upper levels, as it may well be. (Burks, 1928, p. 307)

The geneticist Sewell Wright (1931) later performed a genetical analysis, using his method of ‘path coefficients’, on Burks’ data. He showed that Burks’ correlation between environment and adopted child’s IQ could be broken down into two components: the direct effect of home environment on IQ and the indirect effects of the foster parents’ IQ on the child’s environment. The direct correlation of home environment and child’s IQ was 0.29; that is, about 9 percent of the IQ variance was attributable to variance in home environments, independently of the intelligence of the foster parents. The SD of these environmental effects thus would be equivalent to 4.39 IQ points and the total reaction range of home environments on IQ would be approximately this value multiplied by the number of SDs in a normal distribution, or 4.39 x 6 = 26.34 IQ points. (If the indirect effects of foster parents’ IQ is included with the direct effects of home environment, the total reaction range is 36 IQ points.) The occupational status of the foster parents in Burks’ study spanned a wide range, from professional to unskilled labor, although a majority were in occupations that would be classified as middle- and upper-middle SES. The reaction range of 26 means, in effect, that improvement of a child’s home environment (without changing his parents’ IQs) would raise the IQ 26 points for those children who shortly after birth are moved from the most unfavorable environment in a thousand to the most favorable environment in a thousand. A gain of 36 points would occur if, in addition, the child exchanged the ‘worst’ parents in a thousand for the ‘best’ parents in a thousand.

Chapter 8

Multiple and Partial Correlation Methods

… A study by Tenopyr (1967) is interesting because it involves control of SES both by selection of subjects and by statistically partialling out SES from the correlations between race and abilities. The subjects were 167 Negro and white machine-shop trainees recruited from the low socioeconomic areas of the community (Los Angeles). They had an average of 11.9 years of education and their mother’s average education was 11.1 years. The whites were slightly but not significantly lower than the Negroes on a composite SES index based on the education of the subject, his mother’s education, and the status level of his father’s job. In addition to the SES index, three ability tests were given to all subjects: Verbal Comprehension (V), Numerical Ability (N), and Spatial Visualization (S). The correlations among all the variables are as follows:

From these above correlations, we can obtain the following partial correlations: [3]

rV, Race.SES = 0.30 p < 0.01
rV, SES.Race = 0.24 p < 0.01

rN, Race.SES = 0.19 p < 0.01
rN, SES.Race = 0.16 p < 0.05

rS, SES.Race = 0.21 p < 0.01
rS, SES.Race = 0.06 n.s.
rS, Race.SES, V = 0.19 p < 0.01

All correlations are rather low due to restriction of the range on all variables caused by the method of subject selection. But the partial correlations remain interesting. Note that every test has a higher partial correlation with race than with SES and that the difference is largest for the spatial ability test, which is the least culturally and educationally loaded of the three. Also note that partialling out both SES and Verbal Ability (the most culturally loaded test) still leaves a significant partial r of 0.19 between race and spatial ability. In other words, the racial difference on all of these tests cannot be accounted for by whatever environmental influences are summarized in the SES index. Moreover, it should be remembered that since SES most probably has some correlation with the genetic component of ability, when we partial out SES from the correlation of race with ability we are partialling out too much; that is, we remove something more than just the environmental component of the correlation between SES and ability.

Much higher correlations than Tenopyr’s between race, SES, and IQ are available from large unselected samples of Negro (N = 655) and white (N = 628) school children in Georgia (Osborne, 1970): IQ was measured by a group test (California Test of Mental Maturity) and SES was measured on a rather elaborate 25 item questionnaire. Race is quantized as Negro = 0, white =1. The correlations are:

rRace, IQ = 0.691
rSES, IQ = 0.615
rRace, SES = 0.638

The partial correlations are:

rRace, IQ.SES = 0.493
rSES, IQ.Race = 0.312

The point-biserial correlation of 0.493 between race and IQ with SES partialled out corresponds to a mean IQ difference between the races of about 1σ. (Figure 8.1 shows the relationship between the point-biserial correlation, r_pbs, and mean group difference, d, in sigma units, when the two groups have equal Ns and equal σs.) The correlation of SES and IQ with race partialled out is significantly smaller than the correlation between race and IQ with SES partialled out. All this can mean is that the environmental factors summarized in the SES index at most account for (0.691)² – (0.493)² = 0.23 of the total IQ variance which is associated with SES differences between races.

This value of environmental variance between the races is close to twice the estimates of between-families environmental variance within races. In other words, the environmental index (SES) accounts for only about as much of the mean racial differences as would be accounted for if we assumed that the between-groups heritability is about the same as the within-groups heritability, i.e., both the between-groups and within-groups differences are comprised of about 20 to 25 percent environmental variance. Notice that the correlation between SES and IQ (with race partialled out) is 0.312, so that SES accounts for about 0.10 (i.e., r²) of the variance in IQ within racial groups – a value slightly greater than estimates of between-families environmental variance (e.g., Jensen, 1967). And this is about what should be expected, since the SES index reflects the between-families part of the environmental variance. The environmental difference between the racial groups is treated as a part of the between-families variance when the data of both groups are analyzed together, as we have done here. These results from Osborne’s study, then, are consistent with the hypothesis that the between-racial-groups heritability is about the same as within-groups heritability. [...]

Chapter 9

Intelligence of Racial Hybrids

American Negroes are racial hybrids. In 1926 Herskovits found that 70 percent of a U.S. Negro sample reported having one or more white ancestors (Herskovits, 1926), and in 1969, T.E. Reed, a leading student of this subject, asserted that there are probably no Negroes of pure African descent being born in the United States today, unless they are born to African exchange students (Reed, 1969a). Reed states that the American Negro usually has ‘between 2 and 50 percent of his genes from Caucasian ancestors, and these genes were very probably received after 1700’ (Reed, 1969a, p. 165). … Today the average percentage of Caucasian genes in American Negroes is estimated, on the basis of blood groups, at something between 20 and 30 percent. (These estimates are based largely on population samples from northern urban areas.) … The most representative estimate is probably that of Negroes in Oakland, California, with 22 percent Caucasian genes. Due mainly to selective migration, the percentages differ in various parts of the country, being generally lowest in the ‘Deep South’ and highest in the North and the West. The average in two countries in Georgia is 11 percent. Representative samples in other localities are New York (19 percent), Detroit (26 percent), Baltimore (22-31 percent), Chicago (13 percent), Washington and Baltimore (20-24 percent), Charleston, South Carolina (4-8 percent). Within each of these Negro subpopulations there is considerable variability among individuals in their percentage of Caucasian genes. The Oakland, California Negro population, with its mean of 22 percent Caucasian genes, has an estimated standard deviation of 14 percent (Shockley, 1970b), which means that the variability of the degree of Caucasian admixture among the California Negroes is at least as great as the average differences in Caucasian admixture between Negroes in the South and those in the North and West. The frequency of genes of African origin in the white population, on the other hand, is estimated at less than 1 (Reed, 1969b).

SKIN COLOR AND IQ

… Estimates of the correlation of skin color in Negroes with amount of Caucasian ancestry are about 0.30 to 0.40. Thus, in terms of measurement theory, where the reliability of a measurement is the square of the correlation between true score and the observed score, the reliability of skin color (‘observed score’) as an index of Caucasian ancestry (‘true score’) would be at most about 0.40² or 0.16. If now we hypothesize that there is a correlation between Negroes’ IQs and the amount of their Caucasian ancestry and that this correlation is slightly higher than for skin color (since more genes are involved in intelligence), say about 0.50 as an upper limit of the correlation, the reliability of IQ as an index of Caucasian ancestry would be about 0.50² or 0.25. The highest correlation that can be obtained between two measures is the square root of the product of their reliabilities. So the highest correlation we could expect to find between IQ and skin color would be about SQRT[(0.16)(0.25)] = 0.20. Any higher correlation than this would most probably be attributable to factors other than racial admixture per se. [...]

Shuey (1966) has reviewed all the studies which attempted to relate IQ to skin color in racial hybrids. In 12 of the 18 studies, the hybrids lighter in color score higher than the darker; in 4 other studies the lighter scored higher in the majority of tests given, i.e., in 3 out of 4 or 3 out of 5; and in two of the comparisons there was no evidence of a relationship between the visible indexes of white ancestry and test score. These studies leave little doubt of a true relationship between skin color (and other visible features ranged along a Negroid-Caucasoid continuum) and scores on intelligence tests. The actual correlation between lightness of skin and test scores was determined in several studies, all reviewed by Shuey (1966, pp. 456-63). Correlations range from 0.12 (Klineberg, 1928), to 0.17 (Herskovits, 1926) and 0.18 and 0.30 (Peterson & Lanier, 1929). But, as Herskovits (1926) pointed out, the question that such studies do not answer is the extent to which these correlations are a result of racial admixture. They could be just the result of assortative mating patterns which bring about a genetic correlation between skin color (and other visible characteristics) and intelligence. If lightness of skin is a socially valued characteristic, it would be a factor in assortative mating, along with other factors such as intelligence and its correlates of educational and socioeconomic status. Thus, genes for skin color and for intelligence would become segregated together, resulting in a phenotypic correlation between these two characteristics which would have nothing to do with racial intelligence differences. … Freeman et al. (1966) found a significant positive relationship between lightness of skin and income, socioeconomic status, and educational attainment in Negroes. There was also a correlation between spouses in skin color, showing that this characteristic is a factor in assortative mating in the Negro population. Obviously, to establish any direct correlation between intelligence and degree of Caucasian admixture in Negroes would require the use of non-visible genetic characteristics, which are therefore not a basis for assortative mating or social discrimination, as an index of Caucasian admixture.

OFFSPRINGS OF NEGRO-WHITE MATINGS

[...] Willerman, Naylor, and Myrianthopoulos (1970) compared the IQs of four-year-old children resulting from all four of possible combinations of matings of Negro and white men and women. They found that the interracial offspring of white mothers were significantly higher than of interracial Negro mothers. Nearly all of this effect was due to the very low IQs of the male children of unmarried Negro mothers. Maternal race was a significant factor in the results only among the children of the unmarried Negro mothers, whose children, particularly the males, had the lowest IQs. This findings accords with others showing the greater vulnerability of males of unfavorable prenatal, perinatal, and postnatal conditions (Jensen, 1971b). But the study sheds little, if any, light on racial genetic differences, since there was no measurement of the parental IQs in the two interracial combinations [5] Persons involved in interracial marriages or matings cannot be regarded as representative of the general population of whites or Negroes. For example, a study (reported in Goldhammer, 1971) of racial intermarriages between 1914 and 19338 in Boston showed that Negro grooms were occupationally well above the average employed Negro male, whereas white grooms were occupationally far below employed white males in general. Both white and Negro brides in interracial marriages were occupationally below the average of women in their respective racial groups. In interracial marriages, the average IQ of Negro grooms is probably higher than of white grooms. Thus the higher IQs of interracial children born to white mothers could be due to the genetic effect of the superior Negro father rather than to any prenatal or postnatal environmental advantage afforded by having a white mother.

Chapter 11

Equating for Socioeconomic Variables

[...] Apart from the strictly environmental effect of parental IQ, [1] it is obvious that, since IQ variance contains a large genetic component, equating groups for parental IQ means equating them for genetic factors more than for environmental factors. The same is true, though to a lesser degree, when we equate for SES. When typical Negro children are equated with white children on some index of SES, one is comparing a majority of the Negro population with some lower fraction of the white population. [2] The white comparison group, therefore, is not genetically representative of the entire white population but is genotypically (as well as environmentally) lower by some substantial degree. [..]

… If SES per se were an important environmental determinant of IQ, we should expect children’s IQs to correlate at least as much with the SES of their parents as with the SES the children attain as adults, but this is far from being the case. Burt (1961b) found in England that approximately 30 percent of the population changes SES (half going up and half going down) in each generation (based on father’s occupation divided into six classes, from ‘higher professional’ to ‘unskilled labor’). There is probably similar intergenerational mobility in the United States, at least in the white population. In Minnesota, for example, Waller (1971b) found a correlation of 0.724 between men’s IQs (measured when they were in high school) and their own fathers’ adult occupations but a correlation of only 0.32 between their IQs and their own fathers’ adult occupations. (The corresponding correlations in an English population were 0.77 and 0.36 [Burt, 1961b].) The SD of parental IQs within occupational classes is generally much less (about one-half) than that of chlidren’s IQs within occupational classes, which is usually only one or two points less than the SD of the total population (see Gottesman, 1968). This very great variance of children’s IQs within each class is embarrassing to environmental theories. It is predictable from the polygenic theory of intelligence. [...]

Although matching for SES in comparing racial groups most likely works against a genetic hypothesis of the racial difference, because it matches to some degree for genetic as well as environmental factors, it is nevertheless instructive to note the results of studies which have attempted to control for SES by actual matching or by statistical equating of groups. In reviewing all the studies of this type up to 1965, Shuey (1966, p. 518) summarizes the results as follows:

With two exceptions, the colored averaged below the white groups ni mental test performance in all of the 42 investigations. [The two exceptions were studies which showed ambiguous results or presented insufficient statistical analysis to permit an evaluation.] Average IQs were reported in 33 of the studies including a total of about 7,900 colored and 9,300 white Ss, and from these a mean difference of 11 points favoring the whites was obtained [in contrast to a mean difference of 15-16 IQ points when random samples are compared]. . . . Twenty-five of the 41 studies were located in the North, and in at least fourteen of the researches the colored and white children were not only attending the same school, but were living in the same district or neighborhood. The combined mean difference in IQ between the 2,760 colored subjects tested in the North and the whites of comparable socioeconomic status or occupation was 7.6. Nearly all of these Ss in the eighteen studies were of school age, the whites and Negroes attending the same school and living in the same areas, many with large Negro populations.

… Shuey (p. 519) continues: ‘The combined mean difference in IQ between the 617 colored Ss of higher status and their white counterparts is 20.3, in contrast with a combined mean difference of 12.2 between the 3,374 colored and 2,293 white children of low status.’ Overall, the mean IQ of the high status Negro children is 2.6 points below the mean IQ of the low status white. [4] Since the publication of Shuey’s review in 1966, this finding has been repeated in three major studies based on very large samples (Coleman et al., 1966; Wilson, 1967; Scarr-Salapatek, 1971a).

NOTES

1. The environmental contribution of parental IQ can best be assessed by means of adopted or foster children, since there is little or no genetic correlation between foster children and their foster parents. In a study of this kind by (Burks) 1928, it was found that the total environmental contribution to te IQs of the foster children was only 17 percent (which is close to 1-h² when h² is based on twin studies.) The independent environmental contribution of parents’ intelligence (mother and father combined) was about 3 percent. Burks (1928, p. 301) states: ‘We should not expect this environmental contribution of parental intelligence to be over four or five percent, however, because the correlations (even when corrected for attenuation) between child’s IQ and foster parents’ M.A. (mental age) are so very low.’ The correlation was 0.09 for foster father and 0.23 for foster mother. A study by Honzik (1957) showed approximately the same correlation between foster children and their biological parents, with whom they have had no contact since birth, as found for children reared by their own parents. The adopted children did no correlate significantly with their adopting parents. In the frequently cited study by Skodak and Skeels (1949), children of rather low IQ mothers showed a correlation of 0.38 with their true mothers with whom they had no contact beyond infancy. The adopted children’s average IQ, however, was approximately 11 points higher than the mean IQ that would be predicted from a genetic model assuming that the children represented a random selection of the offspring of mothers with a mean IQ of 85 and were placed in randomly selected environments in the population. Actually, of course, these children were selected by the adoption agency as suitable for adoption and the adoptive homes were selected for their favorable environmental attributes. The 11 points, however, is very likely an overestimate of any environmental effect on these children’s IQs, since the children put out for adoption, most of them illegitimate, were not a random selection of such children, and it has been indicated by Leahy (1935) that illegitimate children who become adopted have a higher average IQ than illegitimate children in general or than legitimate children placed for adoption. Readers interested in a detailed an trenchant critique of the Skodak and Skeels studies should read Terman (1940, pp. 426-7) and McNemar (1940).

4. Shuey (1966, p. 520, footnote 55) gives the following means (of children’s scores) for the combined studies:

Assuming a single parent-offspring regression of 0.50 and no assortative mating, which is the simplest possible genetic model, and assuming a white population mean of 100 and a Negro population mean of 85, the mean IQs of the most extreme parent (probably the father or the one who chiefly determines the family’s SES) are estimated as follows:

Chapter 12

Accentuated Environmental Inequalities

On all the socioeconomic, educational, and health factors which sociologists have generally pointed to as causes of the Negro-white differences in IQ and scholastic achievement, the American Indian population has been about as far below Negro standards as the Negro ranks below whites. In 1960 Indian median income was 59 percent of Negro, which was 55 percent of white. Life expectancy, reflecting nutrition and health care, is much lower for Indians than for Negroes. In educational disadvantages, unemployment, poor housing, and infant mortality Indians are considerably worse off than Negroes. The Coleman Report (1966) used a scale composed of 12 categories of environmental variables [1] deemed important by social scientists as having a causal relationship to children’s intellectual development. In this nationwide survey, which included more than 645,000 children in 4,000 public schools, Indians were lower than Negroes in all 12 environmental categories, and, overall, Indians averaged further below Negroes than Negroes averaged below whites. The relevance of these environmental indices is shown by the fact that within each ethnic group they correlate in the expected direction with tests of intelligence and scholastic achievement. Since health, parental education, employment and family income, in addition to the 12 more subtle environmental factors rated in the Coleman study, are all deemed important for children’s scholastic success, the stark deprivation of the Indian minority even by Negro standards ought to be reflected in a comparison of the intelligence and achievement test performance of Indians and Negroes. The interesting fact is, however, that on all tests, from first to twelfth grade, Indians scored higher than Negroes. Since many Indian children are bilingual, they can be most fairly compared with white and Negro children on non-verbal tests of intelligence, especially in the early school years. Coleman et al. (1966, p. 20) found that on a non-verbal intelligence test the mean score of Indian children in the first grade (approximately 6 years of age) exceeded the mean score of Negro children by 0.96 SDs, which is equivalent to about 14 IQ points. [...]

It can be seen in Table 12.1 that at every grade level from 1 to 8 the Negro group is further below the white group than is the Mexican group, and the difference is greater for the non-verbal tests than for scholastic achievement tests. Yet on the Home Index, the Mexicans are further below the Negroes than the Negroes are below the whites. The relevance of the Home Index is shown by its positive correlations with test performance within groups, and in a multiple-regression equation for predicting scholastic achievement the Home Index makes a unique contribution to the overall prediction of achievement. Also a questionnaire similar to that used in the Coleman study to reflect attitudes of self-confidence, self-esteem, and educational aspirations showed only small Negro-white differences, while scores were generally much lower for the Mexican group. None of these indices reflects the added disadvantage of the Mexicans’ bilingualism. In the present sample, the percentage of Mexican children whose parents speak only English at home is 19.7 percent as compared with 96.5 percent for whites and 98.2 percent for Negroes. In 14.2 percent of the Mexican homes Spanish or another foreign language is spoken, as compared with 1.1 percent for whites and 0.5 percent for Negroes. Many of the parents of the Mexican children grew up in Mexico where they had little or no education. [...]

On Raven’s Progressive Matrices, a non-verbal, culture-fair test of the g factor of intelligence, the Mexicans were intermediate between whites and Negroes, as shown in Figure 12.1, despite the lower SES and poorer motivation of the Mexican pupils.

Finally, a factor analysis was performed on the intercorrelations among all the variavles in all three ethnic groups combines. Four major factors emerged: (I) scholastic achievement and verbal intelligence, (II) non-verbal intelligence, (III) rote memory ability, (IV) socioeconomic status. Minor factors were (1) speed, motivation, and persistence, (2) neuroticism, (3) extraversion, (4) age in months. Since the four major factors are orthogonal (i.e., uncorrelated with one another) by virtue of the type of factor analysis used (varimax rotation of the principal components), each one can be viewed as a ‘pure’ measure of a particular factor in the sense that the influences of all the other factors are held constant. Factor scores were obtained for every pupil on each of the four main factors. (The factor scores have an overall mean of 50 and a standard deviation of 10.) The mean factor scores of the three ethnic groups are shown for grades 4, 5, and 6 (total N = 1,179) in Figure 12.2. On factor I (verbal IQ and achievement) all three ethnic groups differ significantly from one another. On Factor II (non-verbal IQ) the Negro-white and Negro-Mexican differences are significant, but the Mexican-white difference is not. On Factor III (rote memory) the only significant difference is between Mexicans and Negroes at grades 4 and 5. On Factor IV (SES) the Mexicans fall significantly below whites and Negroes, whose SES factor scores differ only slightly in this school population.

Chapter 13

Inequality of Schooling

Statistics based on all schools (over 900) in New York City show a strong negative correlation between pupil expenditures and scholastic achievement, since the school’s financial resources are positively correlated with the proportion of Negro and Puerto Rican enrolment (Gittell, 1971). The 30 elementary schools in New York with a per pupil expenditure of more than $1,100 per year (mean of 11,330) showed reading and arithmetic scores five to seven months below the scores of pupils in the 101 schools with an expenditure below $600 (mean of $551). Pupil-teacher ratios in the high-scoring schools were more than twice as high as in the low-scoring schools. In other words, by most objective indices of advantages provided by the majority of schools in New York, the minority children are more favored than majority children. The report states:

The evidence we have accumulated is somewhat surprising. We have recorded traditional variables that supposedly affect the quality of learning: class size, school expenditure, pupil/teacher ratio, condition of building, teacher experience, and the like. Yet, there seems to be no direct relationship between these school measurements and performance. Schools that have exceptionally small class registers, staffed with experienced teachers, spend more money per pupil, and possess modern facilities do not reflect exceptional academic competence. (Gittell, 1971, p. 2)

Jensen (1971a) compared large representative samples of Negro and Mexican-American pupils with white pupils from kindergarten through eighth grade in largely de facto segregated schools in the same California school district, using a comprehensive battery of tests of mental abilities and of scholastic achievement, in addition to personality inventories and indices of socioeconomic and cultural disadvantage. It was found that when certain ability and background factors over which the schools have little or no influence are statistically controlled, there are no appreciable differences between the scholastic achievements of minority and majority pupils. The study lends no support to the hypothesis that the schools are discriminating unfavorably against Negro pupils, whose average scholastic achievement was 0.66 SD below the white mean. (On non-verbal tests of intelligence, the average difference was 1.08 SD.) Furthermore, it was found that Negro children are as far below the white IQ mean, in sigma units, at kindergarten or first grade as at twelfth grade. If the schools contributed to the Negro-white IQ difference, one should expect to find an increase in the difference from kindergarten to twelfth grade. When race is entered as a variable into a multiple regression equation, along with a number of measures of mental ability and social background, to predict scholastic achievement, race per se makes no significant independent contribution to the prediction. This means, in effect, that a Negro pupil and a white pupil who are matched for IQ and home background will perform equally well in school. [...]

… I believe there has been some reduction in the achievement gap in the California schools in which I have collected data and where there has been a concerted effort to give every advantage to Negro children.

Chapter 14

Teacher Expectancy

To date there have been nine attempts all together to replicate the Rosenthal and Jacobson (RJ) Pygmalion effect. Elashoff and Snow (1971, pp. 158-9) in their review of these studies concluded

. . . it can be seen that of nine studies (other than RJ) attempting to demonstrate teacher expectancy effects on IQ, none has succeeded. Of twelve expectancy studies including pupil achievement measures as criteria, six have succeeded. Of seven studies including measures of observable pupil behavior, three have succeeded. And of seventeen studies including measures of observable teacher expectancy effects are most likely to influence proximal variables (those ‘closest’ in a psychological sense to the source of effect, e.g., teacher behavior) and progressively less likely to influence distal variables (or variables psychologically remote from the source of expectations). IQ, the most remote of pupil variables, is unlikely to be affected. These results are consistent with a Brunswikian view of teacher-learner interaction. . . . They suggest that teacher expectancies may be important and are certainly deserving of study, but they fail utterly to support Pygmalion’s celebrated effect on IQ.

Chapter 15

Motivational Factors

SELF-CONCEPT

The study which has used what is probably the most elaborate and most reliable index of self-esteem, the 42-item Coopersmith Self-Esteem Inventory, administered to groups of white, Negro, and Puerto Rican fifth and sixth graders matched for SES and IQ, came to this conclusion:

Support was thus given for the growing number of studies which indicate that the self-concept of Negro children does not differ significantly from and may even be higher than that of white children. It also appears that the self-concept of Puerto Rican children is significantly lower not only than the self-concept of white children, as shown in the minimal amount of previous research, but also than that of Negro children. (Zirkel & Moses, 1971, p. 260)

COMPETITION AND FAILURE THREAT

The several experiments of Katz and his co-workers (recently reviewed by Sattler, 1970) [1] did not use intelligence tests, but timed experimental tasks depending mainly on speed of performance, rather than mental power. Such speed tasks are known to be more sensitive to distractions, emotional states, and the like. One of the tests, for example, was simple arithmetic – but the subjects were college students. This makes sense in terms of the effect Katz was trying to detect in his experiment. The aim was to use a test which was so easy that no intelligence but mainly a speed factor, highky sensitive to distraction, would be the greatest source of variance in the experiment. The experimental tasks that come closest to resembling anything found in standard intelligence tests are the digit-letter substitution and digit-symbol tests, which resemble the digit-symbol subtest of the Wechsler Intelligence Scale. But of the eleven subtests comprising the Wechsler, digit symbol has by far the lowest loading on g (correlated for attenuation) and the lowest correlation of any subtest with the total IQ. … Moreover, Katz used Negro college students, and since college sutdents are selected mainly for intelligence, this would have the effect of narrowing the range of variance that intelligence might contribute to performance on the tests, permitting personality and emotional factors to contribute a relatively larger proportion of the variance. … The magnitude of the score decrements found by Katz, even under the most extremely unfavorable conditions, are small in relation to the standard deviation in the population and do not invariably show up in the predicted direction from one experiment to another.

RACE OF EXAMINER

Shuey (1966) compared the nineteen studies of Negro IQ in elementary school children in the South where the testing was done by a Negro with the results obtained on all Southern Negro school children. Shuey concludes:

The 2,360 elementary school children tested by Negroes earned a mean IQ of 80.9 as compared with a combined mean of 80.6 earned by more than 30,000 Southern Negro school children, an undetermined but probably a large number of whom were tested by white investigators. The present writer also calculated the combined mean IQ achieved by 1,796 Southern colored high school pupils who were tested by Negro adults. This was 82.9 as compared with a mean of 82.1 secured by nearly 9,000 Southern colored high school students, many of whom were examined by white researchers. From these comparisons it would seem that the intelligence score of a Negro school child or high school pupil has not been adversely affected by the presence of a white tester. (p. 507)

DIFFERENTIAL TEST PERFORMANCE

Jensen (1968b) has shown, for example, that Negro pre-schoolers with a mean IQ nineteen points below white children perform equal to the whites on tests of memory span – when the latter tests are given under the same conditions and by the same examiner as the IQ tests. But a factor analysis showed that the memory tests were not measures of intelligence; they involve another kind of mental ability. In this study, the memory test actually called for more attention and freedom from distraction than did the IQ test. Subsequent studies (Jensen, 1970b, c; 1971a; Jensen & Rohwer, 1970) have consistently found smaller or non-significant Negro-white differences on tests of immediate memory while at the same time there were differences of more than one standard deviation on intelligence tests administered by the same testers under the same conditions as the memory tests. If motivational factors or testee and tester interactions affect the intelligence score, one would have to explain why these factors do not affect the memory test scores. It appears that, in general, to the degree that a test does not correlate with intelligence or abstract, conceptual, problem-solving ability, it fails to show a mean difference between Negroes and whites. [...]

A technique that lends itself ideally to this purpose is the free recall of uncategorized and categorized lists, abbreviated FRU and FRC, respectively. The FRU procedure consists of showing the subject twenty familiar and unrelated objects (e.g., ball, book, brush, toy car, gun) one at a time, and after the whole set has been thus exposed, asking the subject to recall as many of the items as he can remember. The same procedure is repeated for five trials, each time presenting the items in a different random order. The subject’s score is the total number of items he recalls correctly on each trial; the items may be recalled in any order that they come to mind. This kind of rote memory, it has been found, shows little or not correlation with IQ. But by a seemingly little change in our set of items, we can turn this procedure into an intelligence test showing a very substantial correlation with standard IQ tests (Glasman, 1968). This is the FRC procedure, which is exactly the same as FRU as regards instructions and requirements of the task. But in FRC the lists are composed of items which can be grouped into several conceptual categories, such as furniture, vehicles, clothing, tableware, etc. The single items, however, are always presented in a random order on each trial without reference to their conceptual categories. The same subjects are never given both FRU and FRC, so there is no basis for any subject’s perceiving one test as being different from the other. Subjects are assigned at random to either the FRU or the FRC test. Both groups have the same examiner, the same instructinos, and to all outward appearances the two tests do not differ in content, difficulty, purpose, or demands made upon the subject. There is no reason whatsoever that FRU and FRC should elicit different test-taking attitudes or motivational states. However, subjects who do not spontaneously tend to ‘cluster’ the items of the FRC list into conceptual categories in recalling them, perform no better on FRC than on FRU. The degree to which a subject ‘clusters’ the items conceptually (a tendency which generally increases from the first to the fifth recall trial) is related to the amount he is able to recall. It is both this amount recalled and especially the conceptual clustering tendency itself which are correlated with IQ. When there is little or no clustering, there is also no appreciable correlation with IQ. It then becomes a test of sheer rote memory, which is psychologically quite different from the g factor of intelligence tests.

When the FRU and FRC procedures were given to groups of Negro and white fourth graders, what was found? First, there was a slight but non-significant (p<0.162) difference between Negro and white scores (i.e., total recall over five trials) in the FRU test (Jensen & Rohwer, 1970, pp. 103-18). On the FRC test, however, the recall score of the white children very significantly (p<0.014) exceeded the Negro mean, by about one standard deviation, as shown in Figure 15.1.

Chapter 16

Language Deprivation

[...] if language differences played the predominant role in the lower intelligence test performance of Negroes, they should obtain their poorest scores on verbal tests and do relatively better on non-verbal and performance tests. In fact, just the opposite is most commonly found. … Every study of Negroes tested with the Wechsler scales reported in the literature, except for those involving non-representative samples such as delinquents and prisoners, show higher Verbal IQ than Performance IQ (Shuey, 1966, pp. 295, 359-60, 371). On the Differential Aptitude Tests, Negro children in New York, whether they are middle-class or lower-class, were found to score higher on the verbal ability test than on any of the other tests (Numerical, Reasoning, Spatial) (Lesser, Fifer, & Clark, 1965).

The nationwide Coleman survey used verbal and non-verbal ability tests from grades 1 to 12 and found overall that Negro children did better (0.2σ to 0.3σ) on the verbal than on the non-verbal tests (Coleman, 1966, Supplemental Appendix, Section 9.10). (All other minority groups – Puerto Rican, Indian, Mexican, and Oriental – showed the opposite. [1]) Moreover, the verbal deprivation hypothesis of Negro IQ deficit should predict that the most disadvantaged Negroes with the lowest IQ – those in the rural South – should show a greater verbal deficit relative to their non-verbal test score than would be found in the comparatively more advantaged Negroes with higher IQs in the urban North. But Coleman actually found just the opposite. The largest disparity between verbal and non-verbal scores, in favor of the verbal, showed up in Negroes of the non-metropolitan South (Coleman et al., 1966, pp. 221-71). Urban Negroes of the Northeast, Midwest, and Western regions, in fact, average two or three points higher on the non-verbal than the verbal tests beyond grade 3. Here, then, is a massive set of data wrhich goes directly counter to the predictions of the verbal deprivation hypothesis: The presumably most deprived Southern Negroes actually do better on the verbal tests, the comparatively least deprived Northern Negroes do better on the nonverbal tests. (On both verbal and non-verbal tests, the Northern and Urban Negroes excel over the Southern Negroes, but the disparity is less on the verbal tests. This appears paradoxical in terms of verbal-environmental deprivation theories of Negro intelligence.)

Do lower-class Negro children fail to understand white or Negro middle-class examiners and teachers, and even their own middle-class schoolmates, because of differences in accent, dialect, and other aspects of language usage? This proposition was examined in an ingenious experiment by Krauss and Rotter (1968). The groups they compared were low SES Negro children in Harlem and middle SES white children in the borough of Queens. Two age levels were used: 7-year-olds and 12-year-olds. Half the children in each group acted as speakers and half as listeners. The speaker’s task was to describe a novel figure presented to him. The listener’s task was to pick out this figure from a multiple-choice set of other figures solely on the basis of the speaker’s description. The novel figures, drawn on cards, were non-representational and were intentionally made difficult to name, so that they would elicit a wide variety of verbal descriptions. The speakers and listeners were paired so as to have every possible combination of age and race (or SES). (It must be remembered that race and SES are completely confounded in this experiment.) The score obtained by each pair of subjects was the number of figures the listener could correctly identify from the speaker’s description. The results: the largest contribution to total variance of scores was the race (or SES) of the listener; the second largest contribution was the age of the listener. In other words, the 7- year-old white (middle SES) children did better as listeners than the 12-year-old Negro (low SES) children. The speaker’s age was the third largest source of variance. The race of the speaker, although a significant source of variance, was less than one-tenth as great as the race of the listener. In both age groups, the rank order of the mean scores for each of the four possible speaker-listener combinations were, from highest to lowest:

White speaker/White listener
Negro speaker/White listener
White speaker/Negro listener
Negro speaker/Negro listener

The authors conclude: ‘. . . no support was obtained for the hypothesis that intra-status communication is more effective than inter-status communication’ (Krauss & Rotter, 1968, p. 173). While these results seem paradoxical in terms of the linguistic difference theories, they could be predicted completely on the basis of mental age obtained on a non-verbal intelligence test, such as Raven’s matrices. The rank order of the means of all possible race x age combinations of speakers and listeners could be predicted by the simple formula MA_S+2MA_L where MA is mental age, S is speaker, and L is listener. This is consistent with the hypothesis that it is intelligence rather than language usage per se which is the more important factor in communication. The results of several other studies of Negro-white differences based on speaker-listener interactions are consistent with this hypothesis and contradict the verbal deficit hypothesis (Harms, 1961; Peisach, 1965; Eisenberg, Berlin, Dill & Sheldon, 1968; Weener, 1969).

Does the disparity between a white middle-class examiner’s standard English and the Negro child’s ghetto dialect work to the disadvantage of the Negro child in a verbally administered individual IQ test such as the Standard-Binet? Quay (1971) attempted to answer this question by having a linguist whose speciality is the Negro dialect translate the Stanford-Binet into the Negro dialect. This form of the test was administered by two Negro male examiners to fifty 4-year-old Negro children in a Head Start program in Philadelphia. Another fifty children, selected at random from the same Head Start classes, were given the test in standard English. The result: no significant difference (Negro dialect form was 0.78 IQ points higher than standard form). The author notes ‘. . . it is interesting that verbal items were passed with greater frequency than performance items. . . .’ ‘The analysis of item difficulty raises questions about the existence of either a language “deficit” or a language “difference” for Negro children having the experiences of the present Ss. At least their comprehension of the standard English of the Binet was not impaired.’ [...]

… As might be expected if deafness constitutes a severe form of verbal and language deprivation, congenitally deaf children score well below normally hearing children on strictly verbal tests. [...]

But how do these deaf children score on non-verbal performance tests of intelligence? Vernon summarizes his review of all the literature on this point: ‘. . . the research of the last fifty years which compares the IQ of the deaf with the hearing and of subgroups of deaf children indicates that when there are no complicating multiple handicaps, the deaf and hard-of-hearing function at approximately the same IQ level on performance tests as do the hearing’ (1968, p. 9), [4] contrary to the popular view that the deaf are retarded, which is correct only as regards verbal tests. But the important thing to note is that the pattern of test scores for the deaf is just the opposite to that of Negro children, who do better on the verbal and poorer on the performance tests.

Chapter 17

Culture-biased Tests

THE CULTURE-BIAS HYPOTHESIS

… McGurk (1953a, 1953b, 1967) … compared the performance of Negro and white 18-year-old high school students on highly culture-loaded as compared with minimally culture-loaded intelligence test items. For this purpose, to quote McGurk (1967, p. 374), ‘A special test was constructed, half the questions of which were rated as depending heavily on cultural background (the culture questions) while the other half were rated as depending little on cultural background (the non-cultural questions). Each set of questions yielded a score – either a culture score or a non-culture score.’ McGurk found that the ‘Negroes performed better (relative to the whites) on the culturally loaded questions’ (p. 378). This comparison was based on Negro and white groups selected in such a manner that ‘Negroes and whites were paired so that the members of each pair – one Negro and one white – were identical or equivalent for fourteen socio-economic factors’ (p. 379). [...]

Examination and statistical analyses of a wide variety of test items reveal that items are graded in difficulty along two main dimensions (not mutually exclusive). One dimension is rarity or infrequency of opportunity to learn the content of the item. Many general information items and vocabulary items vary in difficulty along this rarity dimension, e.g., ‘What is the Bible?’ v. ‘What is the Koran?’ and define ‘physician’ v. ‘philologist’. It happens that the type of items that increase in difficulty along the rarity dimension are those we call the most culture-loaded. Their difficulty depends upon their rarity rather than upon the complexity of the mental processes required for arriving at the correct answer. Complexity is the other main dimension along which test items increase in difficulty. Items differ in the amount of mental manipulation and transformation of the elements of the question that they require in order to arrive at the correct answer. Thus, the question ‘What is the color of fire engines?’ is low on both rarity and complexity, while the question ‘If a fire engine can go no faster than 50 miles per hour, what is the shortest time it could take it to get to a fire five miles away?’ is also low in rarity but considerably higher in complexity. … The rarest, most culture-loaded items involve the least complexity, and the most complex items involve the most common contents. And what we find is that the degree to which items discriminate between social classes and between Negroes and whites is much more a function of the item’s complexity than of its rarity or culture-loading. This is true whether the complexity involves verbal, numerical, or spatial materials. The degree to which test items call for mental manipulation, transformation, conceptualization, and abstraction – and not so much the rarity or culture-loading of their contents – is what mostly determines the Negro-white discriminability of test items. On the other hand, some subpopulations – American Orientals, for example – show just the reverse; they do relatively better (usually exceeding the white population) on those items most heavily loaded on the complexity dimension. Orientals are somewhat disadvantaged on tests to the extent that cultural items are included as opposed to complexity items, while just the opposite typically is true for Negroes.

When many test items of various types are included in a factor analysis, the degree to which they are loaded on the g factor (i.e., the ability factor which is common to all intelligence tests and mainly accounts for their intercorrelations) is related more to the complexity of the items than to the rarity of their contents, especially if the tests are given to a culturally and socioeconomically heterogeneous sample. That is to say, the items that increase in difficulty along the complexity dimension better represent the g factor of intelligence in a heterogeneous population than do the more culture-loaded items. [...]

One of the most status-fair tests, at least for children who are in school and have had experience with paper and pencil, is the Figure Copying Test (see Figure 3.1, p. 78). The child is asked merely to copy the ten forms, each on a separate page, while they are in full view, without time limit. … In factor analyses carried out separately in white, Negro, and Mexican samples, this test has a subtantial g loading in all groups, comparable to that of Raven’s Matrices. … Figure 17.2 shows the scores on this test of several ethnic and social class group totalling nearly ten thousand children in kindergarten to fourth grade in twenty-one California schools. The four ethnic groups are Oriental ( O ), White ( W ), Mexican ( M ), and Negro ( N ). The letter ‘U’ represents schools in an urban, relatively upper-status community socioeconomically as compared with the average school district in California; ‘L’ represents schools in comparatively lower-status rural districts. The groups are ranked on a composite index of socioeconomic status (SES), with SES 1 as the highest, representing largely professional and business-managerial upper-middle-class families. Note that the rank order of SES does not strictly correspond to the rank order of performance in Figure Copying. The Orientals exceed all other groups, and the Mexicans, who are at the bottom in SES, score only slightly below the whites. At fourth grade the range of group mean differences on the test spans more than 2 SDs. Negro fourth graders, on the average, match the performance of Oriental children in the first grade. These findings are consistent with results obtained at Yale’s Gesell Institute using a battery of similar developmental tests with Negro and white elementary school children (Ames & Ilg, 1967). Especially for children who have been exposed to three or four years of schooling, such marked differences in performance would seem most difficult to explain in terms of differential experiences, motivation, and the like.

I have suggested previously that tests which are more culture-fair or status-fair can be thought of as having higher heritability in an environmentally heterogeneous population than highly culture- or status-loaded tests (Jensen, 1968c, pp. 81-6). Evidence from kinship correlations on various tests is consistent with this formulation. For example, standard IQ tests show quite low correlations (about 0.25), and consequently large IQ differences, between genetically unrelated (and thus dissimilar) children reared together, and show quite high correlations (about 0.80), and consequently small IQ differences, between genetically identical twins reared apart. On the other hand, certain highly culture-loaded scholastic achivement tests show much less difference, i.e., rather higher correlations (about 0.50) between unrelated children reared together and lower correlations (about 0.70) between identical twins reared apart (Jensen, 1968a, Table 1 and Figure 1).

[...] If differences are found between groups A and B, one of the three hypotheses can be invoked to explain the difference: (1) the groups are genetically equal but differ environmentally; (2) the groups are environmentally equal but differ genetically; or (3) the groups differ both genetically and environmentally. The consequences of each hypothesis are shown in Figure 17.3. Our hypothetical perfectly culture-free or environment-free (meaning h²=1) test measures the genotype, G: the culture-loaded test measures the phenotype, P. (The phenotypic value, P, is the sum of the genetic and environmental values, i.e., P=G+E.) Assume that the heritability of the phenotype measure, P, is 0.80, so the correlation between genotype and phenotype would be the square root of 0.80, or 0.89. Also assume that the means of the two groups, A and B, differ on the phenotypic measure by 1 SD.

Hypothesis 1, then, is the environmental hypothesis. It states that the mean genotypes of the two groups are either equal (which includes the hypothesis that the phenotypically lower group is genetically equal to or higher than the phenotypically higher group, i.e., G̅_A≤G̅_B) or genotype B is above genotype A, and the average environment of group A is more favorable than that of group B (i.e., E̅_A>E̅_B). If this hypothesis is true, and if h² is 0.80 in each group, then the regression of P on G and of G on P for groups A and B should appear as shown in Figure 17.3 in the two graphs at the top. [3] That is to say, for any value of G, the value of P for group A will exceed that of group B by 1 SD. (The dots represent the bivariate means of groups A and B and the solid and dashed lines are the regression of P on G or G on P.)

Hypothesis 2 is a strictly genetic hypothesis; the groups differ in genotype but not in environment (G̅_A>G̅_B and E̅_A=E̅_B). Here we see that the regression of P on G (and G on P) is the same for both groups.

Hypothesis 3 is a combined genetic and environmental hypothesis, with two parts: (i) group A is more advantaged than group B both genetically and environmentally (G̅_A>G̅_B and E̅_A>E̅_B) and (ii) the genetic difference is greater than the environmental difference (G̅_A-G̅_B > E̅_A-E̅_B). Note that in this case the regression line P_A is above P_B, as in the top left graph (Hypothesis 1), but unlike Hypothesis 1, in Hypothesis 3 the regression line G_A remains above G_B.

Now, with the consequences that logically follow from these three clearly formulated hypotheses made explicit, as shown in the regression lines of Figures 17.3, we can perform an empirical test of these hypotheses. Naturally, we can only crudely approximate the idealized hypothetical regressions shown in these graphs since there are no perfectly culture-free tests, i.e., tests with h² = 1.00. The best we can do at present is to use two tests which differ most conspicuously in culture-loading. (The most culture-loaded test corresponds to P in Figure 17.3 and the least culture-loaded test corresponds to G.) For this purpose we have chosen Raven’s Matrices and the Peabody Picture Vocabulary Test (PPVT). We have already pointed out that the Raven is one of the most culture-reduced tests available. The PPVT provides a striking contrast. It is probably the most culture-loaded among all standardized IQ tests currently in use. The test consists of 150 plates each containing four pictures. The examiner says a word that labels one of the four pictures in each set and the testee is asked to point to the appropriate picture. The items increase in difficulty by increasing the rarity of the pictured objects and their corresponding verbal labels. Figure 17.4 shows the mean frequency of these words per every million words of printed English in American books, magazines, and papers. It can be seen that for both equivalent forms of the test (A and B), the commonness of the words decreases systematically from the first, easy items to the last, most difficult items. [4] The PPVT pictures and labels are almost a parody of culture-biased tests: e.g., kangaroo, caboose, thermos, bronco, kayak, hassock, goblet, binocular, idol, observatory, oasis, walrus, canine.

The Raven and PPVT were given individually to all white (N = 638), Negro (N = 381), and Mexican-American (N = 684) elementary school children in one small California school district. [5] The raw scores on both tests, within 6-month age intervals, were transformed to z scores, with mean =0, SD =1. The regression of Raven on PPVT and of PPVT on Raven was then plotted separately for each ethnic group. The regression lines are perfectly linear throughout the entire range of test scores in all three groups, as shown in Figure 17.5. The slopes of these regression lines of the three groups do not differ significantly, but the intercepts differ significanly beyond the 0.001 level (F = 52.38, df = 2/1658). In short, the differences essential to our hypotheses are fully significant. So let us compare these empirical regression lines with the hypothesized ones in Figure 17.3. First, consider the white-Negro comparison (corresponding to hypothetical groups A and B). We see that the top half of Figure 17.5 corresponds to the right-hand graphs in Figure 17.3. Now we see that in both graphs of Figure 17.3 the white regression line is significantly above the Negro regression line. The only hypothesis to which this situation corresponds if Hypothesis 3 in Figure 17.3. Hypotheses 1 and 2 are both contradicted by the data.

Next, consider the white-Mexican comparison. Here we see that the Mexican regression line is above the white regression line for the regression of Raven on PPVT (upper graph in Figure 17.5), and the Mexican regression line is below the white regression line for the regression of PPVT on Raven (lower graph in Figure 17.5). This state of affairs is predicted only by Hypothesis 1. Thus we see that the results for the Negro-white comparison are predicted by one hypothesis (Hypothesis 3), and the results for the Mexican-white comparison are predicted by another, although both the Negro and Mexican groups are regarded as disadvantaged and score lower than whites on IQ and scholastic achievement tests. [...]

Finally, consider the Negro-Mexican comparison. For the regression of Raven on PPVT the Mexican regression line is above the Negro, but just the reverse is true for the regression of PPVT on Raven. This result corresponds to Hypothesis 1 in Figure 17.3, i.e., the hypothesis GA≤GB and EA>EB, where A and B represent the Negro and Mexican groups, respectively. That is, the finding is consistent with the hypothesis that the Mexican group is genetically equal to or higher than the Negro, but environmentally or culturally disadvantaged relative to the Negro group. Since the Mexican group was also found equal to or higher than the white group genetically in this analysis, and the white gorup is genetically higher than the Negro (i.e., Hypothesis 3), it follows that the Mexican group genetically is not equal to but higher than the Negro. (That is, if Mexican ≥ white > Negro, then Mexican > Negro.) The results are well comprehended within the framework of these alternative hypotheses. Those who think in terms that are exclusively environmental, however, are usually deeply puzzled by the results shown in Figure 17.5. If (in the lower graph) for any given score on the less culture-loaded test (Raven) whites get the highest score on the more loaded-test (PPVT) and Mexicans get the lowest, with Negroes intermediate, it seems to make perfectly good sense from the culture-bias or environmentalist hypothesis. But then when we look at the upper graph in Figure 17.5, we see that for any given score on the culture-loaded test the Mexican gets the highest score on the culture-fair test, and this surely seems to make sense from the environmentalist standpoint. But the Negro group’s regression line does not come next – instead it is well below the white group’s regression line. In other words, if you match Negro, Mexican, and white children on the culture-loaded test, their scores on the more culture-fair test come out with Mexicans highest, Negroes lowest, and whites intermediate. This seems paradoxical to the environmentalist. It is predictable from the hypothesis formulated in Figure 17.3, which involves hypothesizing group differences in both genetic and environmental factors for explaining the Negro-white and Negro-Mexican differences. On the other hand, for these data at least, the hypothesis of only an environmental difference is compatible with the Mexican-white comparison.

Chapter 18

Sensori-motor Differences

REACTION TIME

The overall white-Negro difference is significant (p<0.01). Note that response speed increases with practice, but soon levels off in both groups. The first trials show no Negro-white difference, and the mean difference in the first block of 20 trials is small as compared with later blocks. If motivational and attitudinal factors were acting to depress the performance of the Negro children, it is hard to see why they should have differed so little at th beginning of practice. Increased practice tends to increase and stabilize the magnitude of the difference between the groups.

MOTOR SKILLS LEARNING

Before Noble performed his experiment, a number of relevant factors were already known about pursuit rotor learning. For one thing, this form of learning has not been found to be sensitive to examiner effects; that is, the sex, age, race, and attitude of the experimenter do not significantly affect the subject’s performance. Even so, Noble took precautious in his study. He used both male and female Negro and white experimenters, counterbalanced for all groups in the experiment. (He found no statistically significant effects on tracking performance attributable to sex or race of the examiner.) Also, he minimized any possible experimenter influence by leaving the child alone in the testing room after the instructions were given. (Instructions were given largely by means of demonstration by the experimenter.) As a further check, he recorded the subject’s pulse rate just before and after the learning period, on the assumption that if there were any differences between the groups it would show up in the pulse rate, which is a sensitive indicator of anxiety. There was no race difference and no pre-post test difference in pulse rate. The children were not anxious but actually enjoyed the task and the fun of taking turns and getting out of their regular class activities to participate in the experiment. Also, there was no prior evidence that pursuit rotor learning has any appreciable correlation with intelligence. In a group of 186 boys, for example, McNemar (1933) found a correlation of only 0.17 between tracking ability and IQ. Obviously, not all kinds of learning are as highly related to IQ as is scholastic learning. Finally, it was known that pursuit rotor learning has very high hertability, almost as high as the heritability of height. McNemar (1933) obtained correlations of 0.95 and 0.51, respectively, for MZ and DZ twins. Using the simplest formula of estimating heritability (h² =2(rMZ-rDZ), which assumes no assortative mating for pursuit rotor ability, the value of h² obtained from McNemar’s data is 0.88. Furthermore, Vanderberg (1962) reports that heritability is much higher for pursuit rotor learning with the right hand (or preferred hand) than with the left. In other words, the tracking task can serve either as a test having very high heritability or as a test having low heritability, depending on whether the subject is required to use his preferred or his non-preferred hand.

With this background in mind, Noble had half of each racial group (all were right-handed) perform with their right hand and half of them with their left hand. The results are shown in Figure 18.2. The white subject’s average left-hand performance was slightly better than the Negro’s performance wih the right hand. Also, the race difference is much greater for the right-hand performance, with its higher heritability. So striking and interesting were these results that Noble replicated and extended the study on a new group of 268 subjects, and obtained essentially the same results, significant beyond the 0.001 level: ‘Whites not only performed at a generally higher level of proficiency than Negroes but also were gaining at a faster rate. Even after fifty practice trials conducted under rigorous controlled conditions, the average Negro righ-hand ability was still below the average white left-hand ability’ (Noble, 1969, pp. 22-3).

Noble then went a step further. He divided the Negro group into two groups which we call blacks and mulattoes. He used several genetically independent (but phenotypically correlated) objectively measured physical criteria for this classification, and showed that the groups differed significantly on each one: skin pigmentation, nasal width, lip thickness, hair texture, eye color, jaw formation, interpupillary distance, and ability to taste phenylthicarbamide. The subjects thus classified into three groups showed significantly different mean pursuit rotor scores in the order: whites < mulattoes < blacks. The mean percentage of time on target for the three groups were 4.6 percent, 2.6 percent and 2.1 percent, respectively (Noble, 1968, p. 231. It is not clear from Noble’s account whether these percentages are for the first trial block of six trials or for all trials.) Noble believed that strictly environmental interpretations of these results in terms of socioeconomic and cultural differences would find little evidential support.

Chapter 19

Physical Environment and Mental Development

NUTRITION

I have found a total of only thirteen published studies of the effects of nutrition on mental development. … It is significant that all but one of the studies showing any mental effects of nutritional deficiency were conducted outside the United States in those parts of Africa, Asia, and Central and South America which suffer the most extreme poverty and protein-calorie deficiency. [1] It is interesting that even in these localities the degree of malnutrition sufficient to depress mental development is not found generally in any appreciable segment of any population; these malnourished cases must be sought out in specific families, and even then usually not all the children in the same family will show signs of malnutrition. … Children in whom mental effects of poor nutrition can be demonstrated have seemed almost as hard for researchers to find as identical twins reared apart. The total number reported in the literature is fewer than a thousand, and in only a fraction of these have psychological effects been adequately demonstrated. The problem, of course, is that malnutrition is most often found in families in which frequently other factors, genetic and environmental, that cause mental retardation are also operative. [...]

… Early malnutrition hinders general growth and therefore causes an increased correlation between various physical indices and measures of intelligence. [2] Winick (1970) reported that at 2½ to 5 years of age 70 percent of malnourished children had head circumferences below the tenth percentile – a very skewed distribution indeed – as compared with control children, whose head circumferences showed a normal distribution. Among malnourished children there is a significant correlation between head circumference and IQ, but no significant relationship was found in control children whose head size was within normal limits (Stein & Kassab, 1970, p. 101). Similar effects are found for height; malnutrition, particularly protein deficiency, retards the rate of ossification of cartilage in the first months of life (Platt, 1968, p. 243). Malnutrition also retards early motor development. In every study in which infant development tests, such as the Gesell scale, have been used, they show that the malnourished children score below par. Early malnutrition makes for greater inter-sibling differences; siblings within the same family are not equally affected, but in families in which malnutrition is found, there are significantly larger differences between the siblings as compared with adequately nourished families (Cravioto & Delicardie, 1970). [...]

When a high percentage of low IQs are found among groups of children who themselves have shown no evidence of poor nutrition, it is hypothesized by some investigators that the lower IQs are a result, at least in part, of the children’s mother, or even grandmother, having suffered from poor nutrition. … Stein and Kassab (1970, p. 109) summarize the present state of knowledge on this point: ‘There are no studies in human societies which can be held to support a cumulative generational effect of dietary restriction. Certainly any such effect was not sufficiently widespread, after countless generations of rural poverty, to prevent the emergence during the past century of the technological societies of Europe and North America.’

… The first study, by Harrell, Woodyard, and Gates (1955) was carried out in the Cumberland Mountains of Kentucky and in Norfolk, Virginia. The Kentucky subjects were ‘poor whites’ living in what the authors describe as ‘deplorably low’ economic conditions. The Norfolk subjects all were mothers on welfare, chosen for their low income status; 80 percent were Negro. There were 1,200 mothers in each group. These women were … given a variety of dietary supplements (one group got vitamins; another group got ‘polynutrients’, and the control group got a placebo; i.e., a non-nutritive substance). These dietary supplements were taken throughout pregnancy. The children born to these mothers were given two forms of the Stanford-Binet Intelligence Test, at ages 3 and 4. There were 1,414 children tested in all. The Kentucky children showed no significant effects. (For both tests F<1). The Norfolk children did show significant effects, however. At age 3 the vitamin and polynutrient groups averaged 2.5 to 5 IQ points higher than the placebo group. At 4 years of age the average gain over the placebo group was 5.2 IQ points in the vitamin group and 8.1 points in the polynutrient group. However, for both of these groups and the placebo group there was a significant (P<0.001) decline of 3.04 IQ points between ages 3 and 4. Thus, while the dietary supplements did raise IQ several points over the placebo group, they did not prevent the lowering of IQ between ages 3 and 4. This rapid decline within a one-year period, in addition to the fact that IQ at age 4 accounts for something less than 50 percent of the IQ variance in late adolescence, makes this study inconclusive as to whether any lasting effects on IQ were derived from the dietary supplements during pregnancy. The IQs of the children at ages 3 and 4 were within the typical range for this population, and the decline in IQ from 3 to 4 is also typical; studies of similar groups have found average declines of about 10 IQ points between 3 and 6 years of age (Shuey, 1966, pp. 6-31).

The second study takes a still different approach, which consisted not of looking for children showing malnutrition and determining their psychological characteristics, but rather of finding children in the poorest families in the poorest slums of a large Southern city, Nashville, Tennessee (Carter, Gilmer, Vanderzwaag & Massey, 1971). … The authors describe in general terms the typical backgrounds of the white and Negro families from which their samples were drawn:

The typical family of a white child . . . is likely to be one in which the natural father is present in the home at least 50 percent of the time. He is usually an unskilled laborer or perhaps disabled. The average annual income is below the OEO Poverty Guidelines. Half of the mothers were on Welfare or Aid to Dependent Children Programs. . . . [About 40 percent of the white mothers had completed high school.] The typical black family . . . is likely to be one in which the natural father is not at home. … The average annual family income is about the same as that for the urban white families and is well below the OEO Poverty Guidelines. At least 70 percent of the mothers are receiving Welfare, Aid to Dependent Children, or Social Security payments. The average number of children in the family was about the same as in the . . . white families. [20 percent of the Negro mothers had completed high school.]

No appreciable nutritional difference was found between the Negro and white samples, and both groups were well above the standards recommended by the National Nutrition Survey. … in both groups extremely thorough examination revealed none of the physical or emotional symptoms associated with poor nutrition … With the small samples of this study, the correlations between physical indices and IQ would have too little reliability to be interpretable [...]

If signs of malnutrition were not found in these obviously rather extreme socioeconomically disadvantaged groups, the question naturally arises as to what percent of the United States population, and particularly of the Negro population, suffers from malnutrition to a degree that would affect mental development. [5] … I asked Dr Herbert Birch, a leading researcher in this field, for a rough estimate of the percentage of our population that might suffer a degree of malnutrition sufficient to affect IQ. He said he would guess ‘Not more than about 1 percent’ (personal communication, 19 April 1971). … Assume that all of the 1 percent of malnutrition in the U.S. population occurs within the Negro population; this would mean that approximately 9 percent of the Negro population suffers from malnutrition. Assume further that all 9 percent of this group afflicted by malnutrition has thereby had its IQ lowered by 20 points (which is the difference between severely malnourished and adequately nourished groups in South Africa – the most extreme IQ difference reported in the nutrition literature). Assuming the present Negro mean IQ in the U.S. to be 85, what then would be the mean if the 20 points of IQ were restored to the hypothetical 9 percent who had suffered from intellectually stunting malnutrition? It would be 86.70, or a gain of less than 2 IQ points as an outer-bound estimate. [...]

Actually, no one yet knows what the net effect of undernutrition in an entire large population is under natural conditions in which many concomitant factors are free to operate. One might even hypothesize that the net effect of extreme nutritional depression in a population (not for an individual) might actually be to raise the IQ due to increased fetal loss and infant mortality along with natural selection favoring those who are genetically better endowed physically and mentally. [...]

… Malnutrition retards the ossification of cartilage; yet representative samples of Negro infants have been found to be advanced over whites in ossification (Naylor & Myrianthopoulos, 1967). Malnutrition results in below-normal performance on infant tests of sensori-motor development, yet Negro babies generally show advanced performance on these tests as compared with the white norms. Malnutrition impairs memory ability as well as other cognitive functions, yet Negro children show little or no deficit in rote memory. [...]

… The results, shown in Table 19.1, indicate that there is no appreciable or systematic Negro-white disparity in the magnitudes of the sibling differences and sibling correlations. (The overall Negro-white difference in the value of |d| is 0.15 or 0.01 SD.) A nutritional deprivation hypothesis should predict significantly larger sibling differences (and lower correlations) for Negroes than for whites. This prediction clearly is not borne out by the data. Yet these racial groups differ more than 1 SD in both verbal and non-verbal IQ.

REPRODUCTIVE CASUALTY

… Other groups subjected to poverty have not shown high casualty rates on any index. Mechanic (1968) and Graves et al. (1970) note that Jewish immigrants to America, in spite of their poverty, had even lower rates of infant mortality than any other American group, including the average of the native white population; Orientals are similar in this respect. … Amante et al. (1970) used a number of signs of CNS dysfunction derived from performance on the Bender Gestalt Test to compare Negro and white children in the two lowest SES groups (on a five-category scale). The only significant main effect in the analysis of variance was Race (F = 13.85, p<1); Social Class and the interaction of Race x Social Class were both non-significant (F<1). [...]

At present there are two lines of evidence that seem incompatible with the hypothesis of such a high incidence of brain damage as suggested by Amante et al. and by the many writings of Pasamanick on this subject. The first counterfact is that independently assessed complications of pregnancy are known to be reflected in depressed performance on infant tests of psychomotor development in the first year of life (Honzik, Hutchings & Burnip, 1965). Yet on these very same tests, given at six months to one year of age, large representative samples of Negro infants were found to do as well as, or better than, comparable samples of white infants (Bayley, 1965). Such findings could be compatible with a markedly higher incidence of neurological damage in Negro infants only if it is argued that the Negro infants are normally so very advanced over white infants in psychomotor development that even with a high incidence of brain damage the mean Negro performance is still above the white mean. But this possibility should result in a larger variance of Developmental Quotients for Negroes as compared to whites, and Bayley’s data show no significant racial difference in the variance of DQs.

The second item of evidence which is apparently inconsistent with the hypothesis of high rates of brain damage as a principal cause of lower Negro IQ is the heritability of IQ and the intra-family IQ variance (sibling differences) which are about the same for Negro and white populations. If brain damage is an added external source of environmental variance, it should significantly lower the heritability of IQ and increase sibling differences. Negro and white samples which do not differ significantly on these variables still show an IQ difference of 1 SD or more (Scarr-Salapatek, 1971a; and see Table 19.1, p. 339). [8]

These findings seem to accord with the conclusions drawn by McKeown and Record (1971, p. 52) from their recent review of the literature on prenatal environmental influences on mental development:

Prenatal environmental influences appear to contribute little to the variation in intelligence in a general population from which those with recognized defects are excluded. There is little relationship to abnormalities of pregnancy or labour. . . . But the most convincing evidence that prenatal influences have little effect on measured intelligence is the observation that twins separated from their co-twin at or soon after birth have scores which are little lower than those of single births, in spite of their retarded fetal growth, short period of gestation and increased risks during birth. There are very large variations in intelligence in a general population of births in relation to maternal age and birth order (Fig. 1); but these are due to differences between rather than within families [emphasis added], for there is little variation according to birth rank between sibs.

… In 1965, fetal deaths (for gestation periods of twenty weeks or more) nationwide had almost twice as high a rate among Negroes as among whites (25.8 v. 13.3 per 1,000 live births) … Assuming fetal death to be a threshold effect on a normally distributed variable, the Negro and white populations can be said to show a mean difference of 0.46σ on this variable. … But even if this variable (organismic viability, freedom from impairment, or whatever it is) were perfectly correlated with intelligence, it could account for less than half of the Negro-white IQ difference.

But is the rate of fetal loss in a population entirely a function of external environmental conditions? It appears not to be. [...]

Bresler (1970) has found that the probability of fetal loss is directly related to the degree of genetic heterogeneity among the ancestral gene pools of the fetus. … Bresler established highly significant relationships among three factors: fetal loss, the number of countries in the background of parents, and the distances between birthplaces of parents. [...]

Bresler also found that SES had no significant relationship to percentage of fetal loss in these samples.

[...] Briefly, more distantly related gene pools have greater genetic imbalance between gene loci on the chromosomes; the loci for certain genes do not match up properly, so that if the two alleles required for the production of an enzyme have undergone evolutionary translocations on the chromosomes, the enzyme controlled by a particular gene may not be produced and therefore cannot make its necessary contribution to the normal development of the growing embryo or fetus. Different genes become important at various stages of development, and some genetic imbalances will prove lethal while others will be sublethal but can cause developmental anomalies of varying severity. The effects have been demonstrated, for example, with frogs, all of the same species, but distributed over a wide geographical range. Bresler (1970, p. 24) summarizes some of the findings from these experiments, in which genetic crosses are made between frogs of the same species collected from varying geographic distances:

1. The hybrids between members of adjacent geographical territories tended to be normal in development and morphology.
2. The greater the geographical distance beween parental combinations in eastern North America, the more retarded was the rate of development, the greater were the morphological defects in the hybrids, and the fewer were the normal individuals.
3. The greater the geographical distance between parental combinations, the larger was the percentage of eggs which failed to develop properly.
4. The further apart in geographical distance . . . the members were collected from, the earlier in development did reproductive wastage occur.

… Too close inbreeding causes depression of some characteristics because of the increased likelihood of the pairing of undesirable mutant alleles, while too much heterogeneity of ancestral gene pools can have undesirable consequences due to genetic imbalance caused by translocations and inversions of loci.

NOTES

2. In autopsy studies of stillborn and newborn infants of poor, presumably undernourished mothers in New York City, as compared with infants of non-poor mothers, the magnitude of the effects of ‘poorness’ presumably maternal undernutrition) on the growth of various organs and body measurements was determined. Of the eight measurements made on the babies, the brain was least affected, suggesting that it is probably the nutritionally most highly buffered organ in the fetus (Naeye, Diener, Dellinger & Blanc, 1969). The index of relative effect of prenatal undernutrition for the eight infant body measurements and the placenta were: thymus 38, adrenals 25, spleen 23, heart 15, body length 15, liver 12, kidney 10, brain 6, and placenta 4.