Examining the Measurement Quality of Tests Containing Differentially Functioning Items: Do Biased Items Result in Poor Measurement?
Mary Roznowski and Janet Reith (1999)
This study investigated effects of retaining test items manifesting differential item functioning (DIF) on aspects of the measurement quality and validity of that test’s scores. DIF was evaluated using the Mantel-Haenszel procedure, which allows one to detect items that function differently in two groups of examinees at constant levels of the trait. Multiple composites of DIF- and non-DIF-containing items were created to examine the impact of DIF on the measurement, validity, and predictive relations involving those composites. Criteria used were the American College Testing composite, the Scholastic Aptitude Test (SAT) verbal (SATV), quantitative (SATQ), composite (SATC), and grade point average rank percentile. Results indicate measurement quality of tests is not seriously degraded when items manifesting DIF are retained, even when number of items in the compared composites has been controlled. Implications of results are discussed within the framework of multiple determinants of item responses.
When ability testing was first introduced in the early 20th century, its purpose was to evaluate individuals objectively to distribute scarce resources on the basis of merit, rather than social background, socioeconomic status (SES), or other fallible credentials. Tests were used to assess academic and job-related abilities, skills, and proficiencies to place individuals efficiently and objectively into various educational and organizational positions. Although tests were intended to lead to objective decisions about individuals, they have been found to have adverse impacts on different groups (see Hulin, Drasgow, & Parsons, 1983; Linn, 1982). Individuals from various social and demographic groups tend to perform lower on average than others on certain tests, which has led to claims of discrimination and bias. Being aware of the ramifications of generating and using biased tests, test developers have begun to examine differences found at the item level, commonly referred to as differential item functioning (DIF). After further analysis involving item content is carried out and possible explanations for group differences are examined, undesirable items are considered for elimination from the test.
The assumptions underlying these analyses seem quite reasonable. That is, DIF may have a detrimental effect on the meaning of test scores as well as on the measurement of the underlying trait(s) of interest for various subgroups. However, it becomes important to investigate, in addition to item-level analysis and detection of DIF, the impact of retaining such items on test scores and the meaning of those test scores in terms of measurement quality. It is important to examine group noncomparability at the item level and the extent that lack of comparability carries through to the overall scale or test level. These questions are important because decisions regarding individuals are made at the test-score level and not at the item level. In particular, what are the effects of retaining tests or scales items that function differently for different groups on the measurement quality and correlations involving that test or scale? How detrimental is retaining such items to indexes of measurement quality such as reliability and validity?
Test bias and item bias are discussed frequently as separate phenomena, the concepts rarely being mentioned in the same context (see, however, Humphreys, 1986). (It should be noted at this point that bias will be used throughout this article to indicate items manifesting DIF.) The relationship between test and item bias often has been assumed, although there is little direct empirical evidence to support such an assumption. Test constructors often presume that a test with items determined to be biased by one or more of the various methods necessarily results in a poor test. On the surface, this appears to be a legitimate hypothesis. In fact, this assumption has appeared to be so reasonable that it has been used in the American legal system in historic decisions about educational and employment discrimination. Unfortunately, these and related beliefs frequently have been shown to be inaccurate. Therefore, without empirical evidence, the assumption that a composite of biased items necessarily leads to an invalid or inferior test is largely conjecture and requires empirical evaluation.
According to past research, such an assumption is not always substantiated empirically. It is true that items sharing trait variance but differing widely on other nontrait components of variance frequently are identified as biased against different subgroups. Roznowski (1987) has shown that inclusion in test composites of heterogeneous items, all of which contain systematic, nontrait variance that frequently manifests itself as DIF and/or item bias, still can result in excellent measurement of the trait of interest (general intelligence, in this case). Such results are due to the fact that the nontrait variance may overshadow trait variance in an item, but no single source of bias predominates in the total score. Therefore, in total test score variance, contributions from trait variance are maximized and contributions from bias, or nonrandom error variance, are reduced. This suggests that eliminating such items may, in some cases, even be detrimental to overall test score measurement. However, these ideas need to be systematically examined in empirical research.
Additional evidence questioning the elimination of items with a moderate degree of bias is found in Drasgow’s (1987) research. In this study, several items on the American College Testing (ACT) exam were identified as biased in different directions, either against Whites, Hispanics, Blacks, females, or males. Overall, however, the test provided equivalent measurement for each of the subgroups. In addition, Drasgow (1987) found that statistically significant differences in bias indexes do not necessarily translate into practically significant differences in test scores. In a simulation study of extremely biased in-one-direction-only items and entirely unbiased items, the differences in test scores never exceeded .40 of a standard deviation.
Recent theoretical developments also provide considerable justification for exploring bias at the test level. Shealy and Stout (1991, 1993) showed mathematically that what they call “nuisance” determinants can produce item bias cancellation resulting in little or no bias at the test level. In arguing their position, they discuss “target ability” versus “nuisance” determinants of item response variance, the latter of which are the many nontrait correlates and determinants of item responses in any psychological measure. Indeed, essentially all item responses are multiply determined, and an item can never be a pure measure of a trait. Shealy and Stout (1991) also provided a mechanism for explaining how several individually biased items may or may not combine to exhibit a biasing influence at the test-score level. Their theoretical work shows how cancellation of bias can function to produce negligible bias at the test level. A central position in their work is that bias should be conceptualized, studied, and measured at the test level rather than at the item level.
The current study was undertaken to investigate further the relationship between item bias and test quality. Including items defined as biased in a test composite may not necessarily be detrimental to the measurement quality and predictive validities of that test composite. Instead, when combined into test composites, items manifesting some degree of bias actually may provide adequate measurement of the underlying trait and thus may still result in large and meaningful correlations and predictive relations with important criteria. It must be emphasized, however, that to retain any set of such items, two requirements must be met. First, all items must obviously contain valid, trait-relevant variance. Second, the nontrait variance throughout the items in a given measure should be multiply determined. When both conditions hold, items in a composite should contain more trait variance than any single source of bias variance. This is important at the test/composite level because covariances among all items reflecting the underlying trait of interest will dominate in the composite.
The logic behind this rationale is as follows. Questionable sources of variance in item responses can never be eliminated entirely, but they can be dealt with by systematically maximizing the heterogeneous, trait-relevant components in the test. If items are selected to maximize such trait-relevant heterogeneity, the covariance of any one item with the other items will more likely be determined by target attribute or ability components (Humphreys, 1970, 1986; Roznowski, 1987; Shealy & Stout, 1991) than by any specific, nontrait components. When item scores are combined to form a total score, common variance alone increases in total variance. If the only common determinant among the items is the trait or traits of interest, then trait variance alone increases in total score variance. When the other determinants of the item’s variance are not shared across the set of items, the systematic, nontrait variance is spread across the multiple items, minimizing the influence of any single nontrait contribution to test score variance. Accordingly, it is proposed that items with both attribute variance and systematic error variance can be combined into a composite without detrimental effects on measurement quality and predictive validities.
Although counterintuitive, at the extreme, the scores that result from such a composite of items may in fact better reflect the underlying trait of interest. If all items biased in one or more directions are removed from a composite, a set of items actually may become highly homogeneous in terms of nontrait contributions. The nontrait variance is no longer spread across multiple item responses, all with diverse determinants, which results in the individual sources of nontrait bias variance having a greater impact on the overall test-score variance relative to trait variance. The resulting correlation no longer reflects trait variance alone, but instead may reflect the shared nontrait sources of variance between the test and the criterion (see also Lubinski & Dawis, 1992; Rushton, Brainerd, & Pressley, 1983). This is especially true if the criterion is also a measure made up of a set of highly homogeneous, nontrait-dominated components.
In this study, it is suggested that poor measures of a construct do not necessarily result from the use of items containing systematic bias variance. It is proposed that composites of items manifesting bias can indeed lead to valid and meaningful test scores. To investigate this hypothesis, several contrived composites of biased and unbiased items were developed to satisfy the above requirements. Correlation coefficients and rank order correlations among biased and unbiased composites then were computed and examined within relevant subgroups. Sizeable correlations between composites and the criteria for the various subgroups would indicate support for the idea that bias variance does not necessarily degrade the measurement of the underlying construct as long as valid, trait-relevant variance is present in the composite. Coefficient alphas for the composites also will provide information as to the measurement quality and ultimate utility of the various composites. Regression coefficients and intercepts also will be examined to determine effects on predictive relations involving such biased composites compared to comparable unbiased composites.
Method
Samples
Examinee data from the High School and Beyond (HSB) data set produced by the National Educational Longitudinal Studies Program were used in this study. Participants were selected randomly from a sample of 13,749 high school sophomores who participated in the HSB base year study. Sampling was done for reasons of computational ease and economy and the need to select individuals who had taken a college entrance exam. The final sample consisted of 2,145 high school sophomores. These students were followed up during their senior years and after high school graduation to obtain additional data, which were used for the criterion measures.
Examinee Data
The following aptitude tests were available in the HSB data set: vocabulary (21 items), reading (19 items), basic arithmetic (math1, 28 items), geometry and algebra (math2, 10 items), science (20 items), writing (17 items), and civics (10 items), resulting in a total of 125 items. This data set provided a unique opportunity for the study of item and test properties because item data as well as multiple external criteria were available for a large number of students from highly diverse backgrounds and a wide range of talent. Criteria available were high school grade point average (GPA), high school rank percentile (RANK PERC), ACT exam scores (the ACT compositewas used), and Scholastic Aptitude Test (SAT) scores (SAT math [SATM], SATverbal [SATV], and a composite of both math and verbal tests [SATC]).
Techniques
An estimate of the common odds ratio (ά) determined by the Mantel-Haenszel procedure (Holland & Thayer, 1988) was used to detect differentially functioning items. As a chi-square procedure, the Mantel-Haenszel statistic examines the pattern of responses across discrete levels of the trait. For any comparison of item performance between two groups, the level of the trait essentially is held constant. Therefore, any difference in item performance between two groups denotes differential functioning. Many methods of detecting bias have been proposed and studied (see Linn, Levine, Hastings, & Wardrop, 1981; Lord, 1980; Marascuilo & Slaughter, 1981; Scheuneman, 1979). The common odds ratio was chosen because of its ease of use, its empirical overlap with other methods, and its acceptability as a measure of DIF.
The common odds ratio measures the degree of performance differences between two groups of examinees, the focal and the reference groups. An absence of DIF is represented by ά = 1.00. An item with ά < 1.00 indicates bias against the reference group, and an item with ά > 1.00 indicates bias against the focal group. According to this operationalization of bias, the further an index is from 1.00, the greater is the degree of bias present in the item. For this study, DIF was operationalized as those items with ά < .75 or ά > 1.25. These criteria allowed for the identification of items that were biased against the reference and focal groups to a moderate degree or greater. This operationalization may be criticized as being too moderate. However, it was determined that the majority of the items chosen with these criteria would have been chosen with much stricter criteria. Furthermore, we wanted to be able to select a pool of items containing some degree of bias to spread out the bias correlates and determinants in the overall composites (Humphreys, 1986).
It is important to note here that the odds ratio is asymmetric because the score metric ranges from 0 to infinity, with 1.00 indicating an absence of DIF. For this reason, researchers also look at the negative log odds index. Accordingly, both indexes were examined in these data, with the overlap in terms of classification of items as biased or unbiased being nearly 100%.
DIF was determined for both gender and race (Black, White) analyses. Common odds ratios were computed for the gender analysis with males (n = 1,030) as the reference group and females (n = 1,115) as the focal group. The analysis of racial groups identified White students (n = 1,301) as the reference group and Black students (n = 264) identified as the focal group. Items exhibiting DIF were found in all tests except for the civics test in the race analysis.
Biased composites were created to maximize the degree of DIF. Thus, the contrived composites would provide a fairly powerful test of the impact of DIF on measurement quality and predictive relations. If DIF has a highly detrimental effect on test score measurement, then the nonbiased composites should exhibit markedly better measurement quality and validities than the biased composites. However, if measurement quality and prediction is not systematically affected in the compared composites, then the practice of wide-scale deleting of such items and test “purification” comes into question.
Using both biased and nonbiased items but keeping the number of test items constant across composites being compared, two types of composites were developed for both the gender and the race comparisons. The first set of composites will be referred to as the moderately biased composites and were constructed as follows.
1. All nonbiased items (no bias): Items on all tests for which .75 ≤ ά ≤ 1.25.
2. Items biased against the focal group (focal bias): Items for which ά > 1.25 plus randomly selected nonbiased items, so that the total number of items equaled the number of items in the no bias composite.
3. Items biased against the reference group (referent bias): Items on tests for which ά < .75 plus several nonbiased items, so that the total number of items equaled the number of items in the no bias composite.
4. Items biased against both the focal and the reference groups (both bias): Items on tests for which ά > 1.25 or ά < .75 plus randomly selected nonbiased items, so that the total number of items equaled the number of items in the no bias composite.
It is important to note here that the majority of items selected would have been selected had more stringent criteria been used.
To examine the worst possible case of DIF on measurement quality, a set of extremely biased composites containing only biased items also was developed. If item bias greatly affects the measurement quality and predictive ability of the overall test, this set of composites should reflect this phenomenon. These tests will be referred to as the strongly biased composites and were constructed as follows.
1. All items biased against the focal group (focal bias): Items for which ά > 1.25.
2. All items biased against the reference group (referent bias): Items for which ά < .75.
3. All items biased against both the focal and the reference groups (both bias): Items for which ά > 1.25 or ά < .75.
4. All nonbiased items (focal no bias): Items for which .75 ≤ ά ≤ 1.25 for the focal group so that the number of items equaled the number of items in the focal bias composite.
5. All nonbiased items (referent no bias): Items for which .75 ≤ ά ≤ .25 for the referent group so that the number of items equaled the number of items in the referent bias composite.
6. All nonbiased items (both no bias): Items for which .75 ≤ ά ≤ 1.25 so that the number of items equaled the number of items in the both bias composite.
Following the development of the composites, correlation and regression coefficients for each composite with each criterion variable were computed for the reference and focal groups. Validities and regression coefficients were examined to determine the relative degree of impact retaining bias has on correlations and predictive relations with various valid external criteria. Coefficient alphas were examined to investigate the internal measurement quality of the composites. Finally, rank order correlations were computed between scores on biased composites and scores on the unbiased composites to examine whether dramatic changes in rank orders of observed score distributions would occur with the inclusion of biased items.
Preliminary Analyses
Identification of biased items. The number of items identified as functioning differently for groups was slightly greater in the race comparison than in the gender comparison. In both comparisons, the vocabulary and science subtests contained a large proportion of biased items (kvocabulary = 52%; kscience = 45%). In addition, in the race comparison, the writing subtest contained a large proportion of biased items (kwriting = 47%).
Development of composites. After items were identified as unbiased, biased against the focal group, or biased against the reference group, unit-weighted composites of items were created. Due to the relatively small number of items and thus limited degree of bias in the individual subtests (e.g., reading, math, etc.), this study focused on overall test composites that contained items from all subtests. Overall, 85 items were identified as unbiased in the gender analysis (68%), and 78 items were identified as unbiased in the race analysis (out of 125 total; 62%). The numbers of biased and nonbiased items in the moderately and strongly biased sets of composites for the gender and race analyses are shown in Tables 1 and 2, respectively. Direction of bias refers to the composite type created (i.e., “both” refers to the composite containing items biased in both directions — 39 items biased against both sexes and 46 unbiased items). The second column in each “direction of bias” pair in Table 1 indicates the number of nonbiased items found throughout the various tests. These numbers were used in determining the number of nonbiased items to add to each composite (both, focal, referent) because itwas necessary to create composites of the same size for comparison.
In the moderately biased composites for the gender analysis, the overall both bias composite contained 39 items (46%) biased against males or females and 46 nonbiased items. For the race analysis, the overall both bias composite contained 45 items (58%) biased against Whites or Blacks and 33 nonbiased items.
The focal bias composite for the gender analysis consisted of 22 items (26%) biased against females and 63 nonbiased items. For the race comparison, there were 26 items (33%) biased against Blacks and 52 nonbiased items in the focal bias composite. The third bias composite, referent bias, contained 17 items (20%) identified as biased against males and 68 nonbiased items in the sex comparison. In the race comparison, the referent bias composite consisted of 20 items (26%) biased against Whites and 58 nonbiased items.
In the strongly biased composites, the overall both bias composite contained 22 items biased against females and 16 items biased against males for the gender analysis, for a total of 38 biased items (100% bias). The both no bias composite contained 38 items that exhibited no bias against males or females. The both bias composite for the race comparison consisted of 25 items biased against Blacks and 20 items biased against Whites, for a total of 45 biased items (100% bias). The both no bias composite contained 45 nonbiased items. All bias and no bias composites for the strongly biased comparisons were kept at identical lengths.
The next composites contained items biased against only the appropriate focal group. In the gender analysis, the focal bias composite contained 22 items biased against females, and the focal no bias composite contained 22 nonbiased items. In the race analysis, the focal bias composite contained 25 items biased against Blacks (100% bias), and the focal no bias composite consisted of 25 nonbiased items.
For the strongly biased gender analysis, the referent bias composite contained 16 items biased against males, and the referent no bias composite contained 16 nonbiased items for both males and females (100% bias). For the strongly biased race analysis, the referent bias composite contained 20 items biased against Whites, and the referent no bias composite contained 20 nonbiased items. Notice that in the strongly biased composites, the total number of items was considerably less than that for the moderately biased composites. Also, it is important to note that for the moderately biased analysis, four composites were created, whereas for the strongly biased analysis, six composites were created. In the moderately biased analysis, the following types of composites were created: no bias, both bias, focal bias, and reference bias. In the strongly biased analysis, three biased composites (both, focal, reference) and three unbiased composites (both, focal, reference) were created. It was necessary to create three separate unbiased composites instead of just one in this latter analysis because of the desire to use as many biased items as were available and the need to keep the corresponding biased and unbiased composites equal in length. Thus, the number of items in the biased composites varied, which required a different unbiased composite for each comparison.
Coefficient alphas were computed for the moderately biased composites. These values are presented in Table 3. Overall, alphas are extremely high, all being in the .90s (average alpha is .921). These results, in part, attest to the overall high quality of the various composites constructed, both the biased and the unbiased.
Table 3 also contains the coefficient alphas for the strongly biased composites. These alphas are quite a bit lower than those for the moderately biased composites, which reflects in part the reduced test sizes for these composites. However, the majority of the values are also quite high (average alpha is .78). The alphas are uniformly higher for the more balanced, both-bias composites, with the average alpha being .86. There also appears to be some tendency for the biased composites to have slightly larger coefficient alphas.
Next, rank order correlations were computed for the various bias-no bias pairs for both the moderately and strongly biased composites. These correlations represent ordinal relationships between the rankings of scores for the biased and unbiased tests. Table 4 presents the rank order correlations for the moderately biased composites for both sexes and the combined sample. These correlations are consistently very high, with most correlations being in the high .90s (average r = .97). These results indicate a consistently high degree of overlap for the rank orders of the biased and the unbiased observed score distributions. Thus, individuals’ observed test scores would fall in largely the same relative position in the distribution, regardless of which composite was used (biased or unbiased).
Table 4 also contains the rank order correlations for the strongly biased composites, again with the bias-no bias tests forming the correlated pairs. These correlations are high but quite a bit lower than those for the moderately biased composites (average r = .79). The largest rank order correlations occurred for the more balanced both-bias composites, indicating very similar test score distributions for these more balanced, longer composites (average r = .86).
Next, to investigate the general magnitude of covariance across composites and the overlap between the various contrived composites, it is useful to look at the zero-order correlations between the composites and different criteria. Correlation coefficients were computed for each of the contrived composites and the criterion variables. The criterion variables included scores on the SATM, the SATV, the SATC (a composite of both the math and verbal exams), the ACT, RANK PERC (rank divided by class size), and GPA. All correlations involving GPA were nonsignificant. This being a common finding, a decision was made not to investigate the correlations involving raw GPA.
Correlation coefficients for each composite in the moderately biased set were computed for focal and reference groups. These scores were essentially unit-weighted linear composites of the individual tests that would create relatively long tests for analysis (Shealy & Stout, 1991). The overall composite contained many elements typically found in measures of general ability, although complete factorial coverage cannot be assumed here. Correlations for the moderately biased test composites for males and females are shown in Table 5.
The appropriate comparisons here would involve the no bias composite with the remaining biased composites within each group (i.e., within males, etc.). This type of comparison was viewed as appropriate because of the need to keep extraneous or confounding influences on correlations from unduly influencing results. Excellent validities overall were obtained, which attests to the quality of the HSB measures (average rs for SATC = .82; ACT = .82; RANK PERC = .53). Differences between the correlations of the no bias composite and the focal and reference bias composites as well as the balanced both-bias composites were small. These results indicate that highly similar orderings are occurring for the distributions of the various measures (both the contrived and the criterion scores). Furthermore, differences observed were in both directions, indicating no systematic benefit or detriment from the removal of biased items.
Correlations for the race composites contained in the moderately biased set for Blacks and Whites also are presented in Table 5. Again, excellent validities were obtained overall (average rs for SATC = .84; ACT = .82; RANK PERC = .49). The differences between the correlations of the no bias composite and the focal and referent bias composites are mostly trivial. Recall that all compared composites were designed to have equal numbers of items. Results for both the gender and race comparisons indicate highly similar correlations for both the biased and unbiased tests and thus similar meaning for the different composites within a given group.
Correlations for the strongly biased composites for the gender and race comparisons are provided in Table 6. The differences between the correlation coefficients in the strongly biased set were slightly greater than the differences in the moderately biased composites, as might be expected. However, the validities are quite high even here (average rs for SATC = .76,ACT = .76, RANK PERC = .47 for gender analysis; average rs for SATC = .79, ACT = .77, RANK PERC = .43 for race analysis). Again, these tests were composed of fewer but all biased items. However, note that in some cases, the differences were actually in favor of the biased composites, especially in the gender comparison. If a large degree of DIF was impairing the measurement quality of measures, these comparisons should have detected that impairment. Overall, the differences were trivial, and highly similar validities were obtained for the different composites. Finally, the largest correlations were observed for the more balanced “both” tests (average rs for SATC = .80, ACT = .81,RANKPERC = .50 for gender analysis; average rs for SATC = .82, ACT = .81, RANK PERC = .45 for races).
Regression Analyses
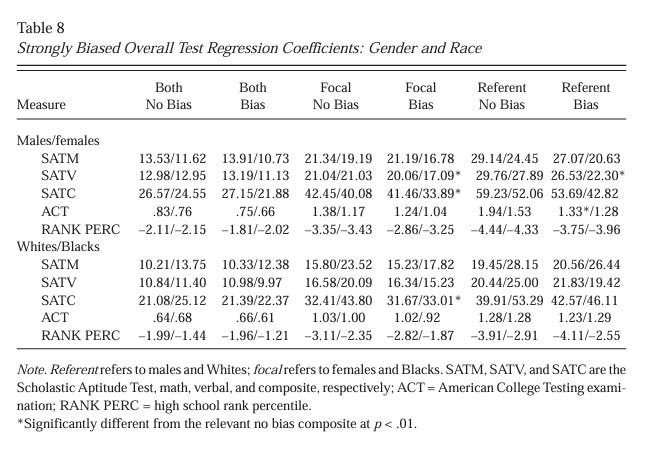
Slopes. Regression equations were computed using each composite to predict each criterion. Regression coefficients were compared across biased and unbiased composites for each examinee group. This comparison was carried out because of the desire to examine differences in decisions that might be made for individuals using the different contrived composites. Regression coefficients (weights) for the moderately biased composites for both the gender and the race analyses are presented in Table 7. Regression weights for the strongly biased composites are presented in Table 8 for the gender analysis and the race analysis. Differences between the slopes of the regression equations across the different composites were evaluated using t tests (Cohen & Cohen, 1983; Pedhazur, 1982). None of the differences for the moderately biased composite regression coefficients was statistically significant for either the gender or the race comparisons (p < .01). Thus, the different composites were yielding highly similar regression weights.
However, in the strongly biased composite, four of the differences in the gender comparison and one of the differences in the race comparison were statistically significant. Again, the relevant comparison here would be the composites for the various bias-no bias pairs. The differences that were found appeared in either the focal or the reference bias composites, but not in the more balanced, both bias composites. It is also important to note that the strongly biased composites were shorter in length than the moderately biased composites. This is relevant because in longer tests, there is likely a greater diversity of nontrait determinants, allowing maximum trait-relevant heterogeneity and common trait variance to increase (Humphreys, 1985).
Intercepts. Last, regression intercepts were explored. Intercepts for the moderately biased composites for both the gender and the race analyses are presented in Table 9. Intercepts for the strongly biased composites are presented in Table 10 for the gender analysis and the race analysis. Some intercept differences were found for the moderately biased tests. However, there are considerably more differences in the gender and race comparisons for the strongly biased test composites. These differences, however, do not appear to be systematic. That is, the differences are not in predictable comparisons or in consistent directions.
Discussion
The impact of differentially functioning items on test scores, test score distributions, and measurement quality often has been assumed to be highly detrimental. Researchers and test developers quite naturally have believed that item-level analyses provide sufficient evidence to make decisions regarding the retention and deletion of items. The results of this study do not support such assumptions. Additional and perhaps simultaneous analyses at the overall test level are necessary for researchers interested in detecting and controlling bias.
The purpose of this study was to evaluate the effects of item bias on two general aspects of the overall test, the measurement quality and predictive validities involving that test. It was proposed that the inclusion of biased items in tests does not greatly weaken or degrade the measurement quality of the test. Does the inclusion of biased items lead to poor measurement? Such questions seem more critical than those at the individual-item level because decisions regarding individuals’ future performance are made at the overall test-score level. The results of this study largely support these premises. The biased test composites produced measurement quality that was, in most cases, equivalent to that of the unbiased test composites. Even with the highly contrived, entirely biased tests, effects on different indexes of measurement quality were not extreme.
Implications
There are several implications, both theoretical and practical, of these results. These findings indicate that the practice of deleting items with some relationship to group membership for the purpose of test purification is not always necessary or beneficial. A test containing items determined to contain some “bias” elements may still provide excellent information about individuals’ future performance. These results can be viewed within the framework of multiple determinants of item responses. Item responses almost always are determined by multiple factors in addition to the underlying trait of interest. Most well-constructed tests contain items whose responses are related to such factors as an examinee’s race, religion, ethnicity, SES, and to a variety of psychological, demographic, or other features of individuals. The presence of such response determinants or correlates does not necessitate removing an item if variance of the item responses is substantially related to the trait being measured. Test developers often delete items identified to be functioning differentially across subgroups so that protected groups are not discriminated against. Frequently, between-group differences on an item or scale indicate little about the relevance of within-group differences on the same items or scales for the measurement of intelligence or other, more specific abilities. Poor measures do not necessarily result from the presence of specific, nontrait components of variance. Problems will likely arise, however, when responses to items in a test are determined in large part by irrelevant and inappropriate factors.
Humphreys (1962, 1970, 1986) has long argued against high homogeneity in psychological tests and in favor of including in tests a heterogeneous set of items, all with trait-relevant variance. He points out that the only reasonable way to keep nontrait determinants from contributing substantially to test scores is to include a diversity of items with heterogeneous determinants. With a constant number of items, the larger the number of different, nontrait determinants, the less any individual determinant will contribute to total test variance. Items sharing determinants will covary with each other and consequently contribute to item-item covariances. The N(N-1) covariance terms will far outweigh the N variance terms that determine total test variance.
Such systematic diversity would serve to increase contributions from attribute or trait sources and to decrease the contribution to total test variance from each systematic, nontrait source and, ultimately, to improve the validity and measurement quality of the test. Eliminating items from a test because their content capitalizes on experiences of or knowledge more likely attained by certain subgroups ultimately may impair a test’s predictive power. In this study, we did not specifically create tests to maximize (or minimize) trait-relevant heterogeneity. However, we think the notion is still relevant here because the contrived composites contained a diversity of content types and required a variety of intellectual and cognitive operations on the part of the examinee.
In addition, it is likely that many items in a given test of ability or aptitude could be identified as biased against some subgroup, either a traditionally protected group or a contrived group. Item analysis can be performed with regard not only to race and gender, but also to socioeconomic group, regional location, type of school attended, number of parents and siblings present in the home, and a potentially endless list of factors. In the current data set, for instance, 91 items out of 125 were determined to be biased against either males, females, minority group members, majority group members, low SES individuals, or high SES individuals. All of these factors, plus myriad others, may indeed be determinants or correlates of item responses in cognitive ability tests. Removing all items that manifest any type of bias can be unnecessarily limiting to test development. The results of this study provide support for the retention of such items, thus allowing test development to be less restrictive. Also, discrimination by omission is less likely.
The current results yielded several “biased” composites that were essentially parallel measures of the compared unbiased composite. The intercept comparisons along with the regression coefficients and correlation comparisons indicate that inclusion of a diverse, heterogeneous pool of items — even biased ones — not only leads to good measurement quality, but also, in many cases, to parallelism. The lack of parallelism found, especially for the extreme composites, could be corrected with adjustments to the intercepts for the problematic test. However, it is true that the slope differences are somewhat more troublesome than intercept differences (Humphreys, 1986). Fortunately, far fewer slope differences were observed.
Also, it is relevant to mention that the differences in measurement quality that were observed appeared in both directions. Thus, when differences do arise, they indicate little consistent or predictable advantage or disadvantage for the biased composites. The question remains as to under what conditions item level bias accumulates to a deleterious level.
Finally, the current findings suggest that test constructors may be able to include in tests more heterogeneous sets of items. As noted in the introduction, a composite of items that share trait-relevant variance but not large amounts of bias variance can serve as an excellent measure of a psychological trait. Because the nontrait or bias variance is not shared among all items, it contributes little to the overall covariance of the items in the test composite, and therefore a better overall measure of the trait is possible. Selecting broadly within the theoretical definitions and limits of the trait domain remains an important and useful strategy for researchers and test constructors working toward the goal of excellent measurement.
Caveats
It is important at this point to discuss some important caveats. We clearly are not recommending that test constructors intentionally create biased items or tests. Nor are we recommending that clearly biased items favoring one group be retained without appropriate off-setting balance in the test. Indeed, the tests created here (especially the strongly biased and biased-in-one-direction tests) were highly contrived and artificial. These are not likely to resemble most tests in current use, and biased items without relatively large trait variance would not be suitable. We simply are stating that measures have the natural and unavoidable tendency of being related to nontrait variables, and this fact does not necessitate the wholesale removal of the offending items. This does not mean that investigations of bias and the characteristics of items that may unfairly penalize members of certain subgroups be discontinued. Such work is obviously important and highly beneficial from a measurement perspective. Researchers need to continue carefully exploring item content for problems leading to problematic differential functioning and work to eliminate these elements as much as possible.
This study, however, should discourage attempts to purge tests of any and all bias, which may indeed be a troublesome and dubious pursuit. It is also important to point out that there is little evidence in these results that indicates that retaining items actually improves measurement quality. Furthermore, the question of whether eliminating bias ultimately degrades measurement has not been addressed.
Also, it bears stating that the current results were based on limited evidence of bias. That is, the Mantel-Haenszel procedure was used alone to detect DIF. The current results would be strengthened through replication using additional operationalizations of DIF.
Conclusions
Several alternative conclusions can be given. It is possible that the indexes of measurement quality used are not sensitive to the effects of bias. Drasgow (1982) has discussed this possibility and has shown the problems that arise when researchers rely on limited evidence for measurement bias. However, an alternative explanation is that our measures are frequently very robust and allow good measurement, even given the unfortunate and inevitable influence of differential functioning at the item level. Also, is it possible that the same biasing factors assumed to exist in the contrived tests are present in the criterion scores? This is obviously a possibility. However, most testing experts agree that scores from the ACT and SAT are among the best measures available, and considerable work has been carried out eliminating the influence of DIF on ACT and SAT scores. Thus, although we cannot rule out this possibility, it seems unlikely given the extremely high quality of the criterion measures used.
Ackerman (1992), Humphreys (1962, 1970, 1986), and Shealy and Stout (1991, 1993) have discussed the related problems of dimensionality and bias of items. These researchers pointed out that the large amount of unique variance in items is not necessarily random error. Shealy and Stout (1991) have conceptualized bias as a sort of multidimensionality involving measurement of a primary dimension and an additional confounding dimension or dimensions. Their work showing how cancellation can function to produce negligible test bias is important and fits well in the framework described in this study.
Further research exploring these and the ideas presented above as well as the issue of simultaneous item and test bias analysis is needed. Future bias research might investigate the question of “How much is too much?” When does item bias accumulate enough to have a clearly detrimental and predictable effect on measurement quality and predictive relations? Furthermore, to build on the work presented here and that of Shealy and Stout (1991), researchers need to address the questions of when bias does not have an offsetting influence and when cancellation does not occur.
Finally, it is important to mention that the current article is focused on one general aspect of testing and decision making: the measurement quality of tests. The article did not address the more problematic and troublesome questions of what is politically fair and appropriate. As discussed by Hulin et al. (1983), it is typically best to separate psychometric from political decisions. Our goal as psychometricians is to create the best possible measures in terms of validity and measurement quality. However, these measures, no matter how meticulously constructed, may result in undesirable differences at the total score level for various groups of interest. The burden then shifts to the test user to make the appropriate decisions, which result in fair compositions of examinee pools.