When observable measures such as socio-economic and health factors are adjusted, the IQ gap is substantially reduced yet a non-trivial difference remains. And while it is known that environmental factors are influenced by genetic factors and therefore should be not treated as pure environmental effects, an outcome that is typically ignored is that the education-matched blacks fall further behind in the IQ scores when education level increases.
Why It Matters
Why this is appalling should be obvious. Environmental and cultural theories typically predict that blacks substantially fall behind whites in cognitive ability due to poor environments preventing lower social class from moving up. There is a cultural disadvantage associated with their neighborhood preventing them from seeking cognitively stimulating environment through books and schooling which according to the social multiplier theory of Dickens & Flynn (2001), would cause their IQ to develop and maintain at high level. The pervasiveness of structural racism across generations, through which blacks are either facing discrimination in health outcomes (Williams & Mohammed, 2013) or public policies such as housing privatization causing a decline in public housing which sometimes leads to school closure (Noguera & Alicea, 2020), has been proposed as one critical factor behind the IQ gap.
All these theories share one common element: they predict that the IQ gap is reducing as one go up in the socioeconomic ladder. Several studies concluded long ago that the increasing gap is therefore challenging for cultural theories (Jensen, 1973, pp. 241-242; 1980, p. 44; Herrnstein & Murray, 1994, p. 288).
To further expand on these old reports, I analyzed 8 data sets: TALENT Project, General Social Survey, Collaborative Perinatal Project, Add Health, High School Longitudinal Study of 2009, Vietnam Experience Study, National Longitudinal Survey of Youth 1979 and 1997 Cohorts.
Explanation of the Analysis
In regression, the common approach is the use of interaction, with eventually squared terms on both the main (i.e., education) and interaction (i.e., group) variables. The problem with this method is that we don't know how reliable (or unreliable) the estimates are at the lowest and highest values of education levels. This is concerning because these categories typically have the lowest sample sizes.
The method I use involve dummy variables instead. Grade or education variables typically range between 10 and 20 categories. If one averages the mother and father's levels, one should consistently approach 20 categories. In each study, I create 10 dummy categories of equal intervals by averaging by two each value of the original education variable. When there are less than 20 units, I average more around the lower and upper ends since they have small sample sizes.
Besides increasing reliability at the lower and upper ends, as well as estimating non-linear relationship, this method allows the confidence intervals and standard errors being estimated for each dummy. The downside though is the requirement of very large sample size if one needs each dummy variable to be reliably estimated.
Certainly, one could easily increase the sample size of each dummy by reducing the number of dummy variables, but then one is facing the risk of imperfect matching. The worst case scenario is blacks being slightly lower than whites in education at the lower end, but much lower than whites at the upper end. This may happen if one splits the original education variable perfectly in half and then goes on to examine the mean IQ score in both categories.
In each study, I select the middle category (usually 5th or 6th) as the reference one, because of its larger sample size. The values of other categories are expressed with respect to this reference category, which must be omitted in the regression to avoid collinearity.
The dependent variable is expressed in z-score, standardized using the white mean and SD. So each dummy will express the z-score gap with respect to the reference category. The “bw” variable expresses the SD gap irrespective of the dummy vars. Positive values of the “bweducd” variables would show evidence of increasing gaps.
One cannot insist more about this. It is extremely important to use sampling weight to recover representativity, and all analyses are weighted using the appropriate weights. Exception being the CPP and VES which don’t have survey weights.
The data and R codes for all of these analyses can be found here. In this file, I also display the results for regressions with interaction and squared terms. They strongly corroborate the pattern we see using the dummy variable approach.
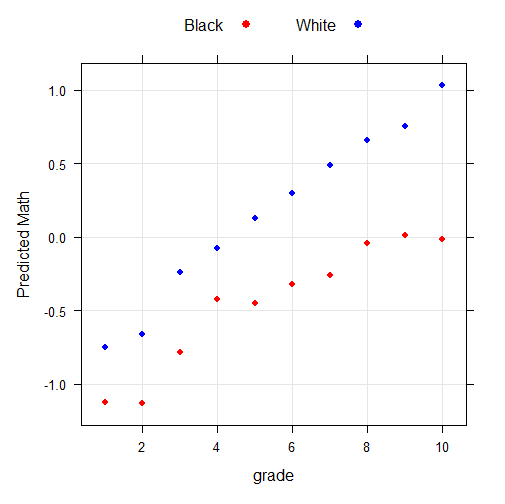
TALENT
N=5,945 blacks and 137,066 whites. The TALENT Project administered various cognitive tests, and their set of tests had been used by Major et al. (2012) in their analysis of the VPR model, but I use here their composite IQ score. Weighted using student weight, BY_WTA.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.07258 0.02661 -40.309 < 2e-16 ***
bw 1.26447 0.02714 46.586 < 2e-16 ***
graded1 -0.41927 0.13184 -3.180 0.00147 **
graded2 -0.31918 0.06508 -4.904 9.38e-07 ***
graded3 -0.07677 0.04859 -1.580 0.11413
graded4 -0.04867 0.03848 -1.265 0.20587
graded6 -0.07605 0.03663 -2.076 0.03788 *
graded7 -0.10761 0.03772 -2.853 0.00433 **
graded8 -0.02518 0.04180 -0.602 0.54688
graded9 0.24391 0.05545 4.399 1.09e-05 ***
graded10 0.51005 0.08207 6.215 5.15e-10 ***
bwgraded1 -0.57409 0.13566 -4.232 2.32e-05 ***
bwgraded2 -0.37639 0.06634 -5.674 1.40e-08 ***
bwgraded3 -0.34733 0.04953 -7.012 2.35e-12 ***
bwgraded4 -0.12770 0.03923 -3.256 0.00113 **
bwgraded6 0.21953 0.03743 5.866 4.48e-09 ***
bwgraded7 0.37164 0.03860 9.627 < 2e-16 ***
bwgraded8 0.37769 0.04283 8.819 < 2e-16 ***
bwgraded9 0.34051 0.05651 6.025 1.69e-09 ***
bwgraded10 0.33796 0.08290 4.077 4.57e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.37 on 142991 degrees of freedom
Multiple R-squared: 0.2078, Adjusted R-squared: 0.2077
F-statistic: 1974 on 19 and 142991 DF, p-value: < 2.2e-16With such a large sample size, it is easy to hit the significance at every levels. But as always, what matters most is the effect size, and it’s huge. Comparing the lowest and upper levels of parents’ education yields a gap increase of 0.9 SD.
GSS
N=2,822 blacks and 15,170 whites. The GSS uses a vocabulary test known as the Wordsum. Because of its low reliability, I used the IRT “g” score from the mirt package, following a 2PL model because a 3PL does not produce reliable parameter estimates in this data. Previously I have shown that the test is minimally biased against blacks. Prior to standardizing, I regressed out the effect of age since age modestly correlates with Wordsum score and blacks in this sample are 1 year-old younger. Weighted using the interaction of wtssall and oversamp.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.00122 0.02871 -34.875 < 2e-16 ***
bw 0.64674 0.03103 20.842 < 2e-16 ***
educd1 0.01188 0.29758 0.040 0.96815
educd2 -1.02515 0.31810 -3.223 0.00127 **
educd3 -0.51250 0.17251 -2.971 0.00297 **
educd4 -0.64497 0.11386 -5.664 1.5e-08 ***
educd5 -0.31032 0.06935 -4.475 7.7e-06 ***
educd7 0.43558 0.04588 9.494 < 2e-16 ***
educd8 0.82748 0.05198 15.919 < 2e-16 ***
educd9 0.76456 0.08718 8.770 < 2e-16 ***
educd10 1.20013 0.12329 9.734 < 2e-16 ***
bweducd1 -0.20515 0.38754 -0.529 0.59656
bweducd2 -0.70224 0.37065 -1.895 0.05816 .
bweducd3 -0.66501 0.20318 -3.273 0.00107 **
bweducd4 -0.03371 0.12291 -0.274 0.78390
bweducd5 -0.08063 0.07721 -1.044 0.29635
bweducd7 -0.08386 0.04970 -1.687 0.09158 .
bweducd8 -0.06409 0.05528 -1.159 0.24638
bweducd9 0.21635 0.09093 2.379 0.01736 *
bweducd10 -0.03896 0.12771 -0.305 0.76032
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8785 on 17972 degrees of freedom
Multiple R-squared: 0.2668, Adjusted R-squared: 0.266
F-statistic: 344.2 on 19 and 17972 DF, p-value: < 2.2e-16There is something odd with the estimate of educd1 as it shows a much higher score than the other lower levels of education, but this may just be a result of chance. The pattern is less clear but if anything is happening, it shows a modest increase in the gap.
CPP
N=19,762 blacks and 18,251 whites. The CPP involves children initially aged 4 with a follow-up study at age 7. They were given the Standford Binet at age 4 and WISC at age 7. I report here the results for age 7 but the results look similar at age 4.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.00746 0.01230 -81.929 < 2e-16 ***
bw 0.69949 0.01871 37.382 < 2e-16 ***
educd1 -0.61430 0.10844 -5.665 1.48e-08 ***
educd2 -0.34598 0.05895 -5.869 4.42e-09 ***
educd3 -0.25292 0.03673 -6.887 5.80e-12 ***
educd4 -0.17779 0.02787 -6.379 1.81e-10 ***
educd5 -0.13320 0.01904 -6.994 2.71e-12 ***
educd7 0.21898 0.01571 13.940 < 2e-16 ***
educd8 0.54766 0.03315 16.519 < 2e-16 ***
educd9 0.82661 0.04896 16.884 < 2e-16 ***
educd10 1.05358 0.12730 8.276 < 2e-16 ***
bweducd1 -0.02379 0.17298 -0.138 0.890599
bweducd2 -0.20843 0.10740 -1.941 0.052291 .
bweducd3 -0.10752 0.06456 -1.665 0.095836 .
bweducd4 -0.21317 0.04898 -4.352 1.35e-05 ***
bweducd5 -0.12157 0.02997 -4.056 5.00e-05 ***
bweducd7 0.07352 0.02377 3.093 0.001984 **
bweducd8 0.14800 0.04193 3.530 0.000417 ***
bweducd9 0.14785 0.05463 2.707 0.006801 **
bweducd10 0.24925 0.13023 1.914 0.055637 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8686 on 37993 degrees of freedom
Multiple R-squared: 0.3165, Adjusted R-squared: 0.3162
F-statistic: 926 on 19 and 37993 DF, p-value: < 2.2e-16As the dummy interaction goes up in values, so does the IQ gap. Ignoring the extremities, the gap at upper levels of parents’ education is about 0.35 SD larger than lower levels.
Add Health
N=853 blacks and 2,526 whites. The Add Health uses a vocabulary test known as the PPVT, administered both in Wave I and III. I report results for Wave III but they look similar in Wave I. Weighted by GSWGT3_2.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.09293 0.11692 -9.347 < 2e-16 ***
bw 1.14224 0.12527 9.118 < 2e-16 ***
educd1 -0.77417 0.20684 -3.743 0.000185 ***
educd2 -0.77727 0.17078 -4.551 5.52e-06 ***
educd3 -0.33023 0.20735 -1.593 0.111335
educd4 -0.21968 0.14248 -1.542 0.123189
educd5 0.15829 0.19600 0.808 0.419390
educd7 0.27970 0.15560 1.797 0.072350 .
educd8 0.36979 0.26192 1.412 0.158094
educd9 0.56971 0.18579 3.066 0.002184 **
educd10 0.63705 0.20577 3.096 0.001978 **
bweducd1 -0.03949 0.25539 -0.155 0.877135
bweducd2 -0.13966 0.19679 -0.710 0.477955
bweducd3 -0.28232 0.22594 -1.250 0.211559
bweducd4 -0.08218 0.15616 -0.526 0.598763
bweducd5 -0.50440 0.20851 -2.419 0.015615 *
bweducd7 -0.24345 0.16840 -1.446 0.148359
bweducd8 -0.12361 0.27494 -0.450 0.653035
bweducd9 -0.16639 0.19683 -0.845 0.397991
bweducd10 -0.08271 0.22290 -0.371 0.710622
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 66.01 on 3359 degrees of freedom
Multiple R-squared: 0.2593, Adjusted R-squared: 0.2551
F-statistic: 61.88 on 19 and 3359 DF, p-value: < 2.2e-16It is probably safe to say here that there is no interaction occurring. Except that the lower and upper ends display a larger verbal IQ gap than middle levels of parents’ education.
HSLS
N=1,507 blacks and 9,341 whites. The HSLS uses mathematics assessments, which provide a measure of achievement in algebraic reasoning. Although it is merely an achievement test, math problem-solving has a good correlation with the Raven’s APM. Weighted by W1PARENT because this one accounts for parent non-response, as I use parent education variable.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.44946 0.05019 -8.955 < 2e-16 ***
bw 0.58001 0.05580 10.395 < 2e-16 ***
educd1 -0.67135 0.08736 -7.685 1.66e-14 ***
educd2 -0.67732 0.11758 -5.760 8.62e-09 ***
educd3 -0.33553 0.05797 -5.788 7.33e-09 ***
educd4 0.02783 0.08955 0.311 0.756002
educd6 0.12653 0.11251 1.125 0.260779
educd7 0.19205 0.08120 2.365 0.018039 *
educd8 0.40702 0.12352 3.295 0.000987 ***
educd9 0.46417 0.12040 3.855 0.000116 ***
educd10 0.43630 0.20896 2.088 0.036829 *
bweducd1 -0.20906 0.11094 -1.884 0.059529 .
bweducd2 -0.11415 0.13042 -0.875 0.381436
bweducd3 -0.03084 0.06517 -0.473 0.636124
bweducd4 -0.23599 0.09776 -2.414 0.015798 *
bweducd6 0.04186 0.12009 0.349 0.727402
bweducd7 0.16835 0.08828 1.907 0.056553 .
bweducd8 0.12291 0.13114 0.937 0.348625
bweducd9 0.16222 0.13033 1.245 0.213280
bweducd10 0.46468 0.22072 2.105 0.035288 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 13.99 on 10614 degrees of freedom
Multiple R-squared: 0.2249, Adjusted R-squared: 0.2235
F-statistic: 162.1 on 19 and 10614 DF, p-value: < 2.2e-16Although most variables lack significance due to sample size issues, the effect size is very large. If we compare the variables bweducd4 and bweducd10, the SD gap increases by 0.7 SD.
VES
N=518 blacks and 3,606 whites. The VES uses Military Technical Test and comprises older people.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.05153 0.10691 -9.835 < 2e-16 ***
bw 1.12765 0.11658 9.673 < 2e-16 ***
educd1 -0.35801 0.57077 -0.627 0.530532
educd2 -0.69187 0.17996 -3.845 0.000123 ***
educd3 -0.60324 0.17298 -3.487 0.000493 ***
educd4 -0.25702 0.12016 -2.139 0.032495 *
educd6 -0.05375 0.13690 -0.393 0.694632
educd7 0.08048 0.18196 0.442 0.658290
educd8 0.70510 0.15262 4.620 3.95e-06 ***
educd9 0.94421 0.28510 3.312 0.000935 ***
educd10 1.11741 0.26189 4.267 2.03e-05 ***
bweducd1 -1.18713 0.57931 -2.049 0.040505 *
bweducd2 -0.52222 0.19347 -2.699 0.006979 **
bweducd3 -0.30436 0.19254 -1.581 0.114013
bweducd4 -0.13421 0.13067 -1.027 0.304438
bweducd6 0.12635 0.14860 0.850 0.395236
bweducd7 0.18112 0.19576 0.925 0.354904
bweducd8 -0.02666 0.16334 -0.163 0.870360
bweducd9 -0.20729 0.30250 -0.685 0.493214
bweducd10 -0.05229 0.27092 -0.193 0.846949
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7929 on 4104 degrees of freedom
Multiple R-squared: 0.4403, Adjusted R-squared: 0.4377
F-statistic: 169.9 on 19 and 4104 DF, p-value: < 2.2e-16One of the smallest sample sizes. Do not expect anything significant, yet the effect sizes show a pattern consistent with other, larger datasets.
NLSY79
N=2,361 blacks and 3,903 whites. The NLSY79 uses the AFQT. I use the NLS custom weights by specifying respondents being in all of the selected years. Since race, AFQT, grade, correspond to different survey years (1979, 1981, 2000), I selected those 3 years in the custom weight.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.27244 0.03472 -36.652 < 2e-16 ***
bw 0.91248 0.03812 23.938 < 2e-16 ***
educd1 -0.34997 0.81315 -0.430 0.666931
educd2 -0.39786 0.33713 -1.180 0.237993
educd3 -0.31866 0.13787 -2.311 0.020845 *
educd4 -0.29734 0.09237 -3.219 0.001293 **
educd6 0.34676 0.08182 4.238 2.29e-05 ***
educd7 0.60889 0.06780 8.980 < 2e-16 ***
educd8 1.05988 0.08575 12.360 < 2e-16 ***
educd9 1.20701 0.13465 8.964 < 2e-16 ***
educd10 1.69136 0.18864 8.966 < 2e-16 ***
bweducd1 -1.18674 0.98444 -1.205 0.228057
bweducd2 -0.79781 0.36037 -2.214 0.026874 *
bweducd3 -0.61398 0.15229 -4.032 5.60e-05 ***
bweducd4 -0.37769 0.10591 -3.566 0.000365 ***
bweducd6 0.10755 0.09040 1.190 0.234231
bweducd7 0.15450 0.07470 2.068 0.038652 *
bweducd8 0.13726 0.09073 1.513 0.130378
bweducd9 0.13610 0.13983 0.973 0.330403
bweducd10 -0.12708 0.19531 -0.651 0.515310
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 513.4 on 6206 degrees of freedom
Multiple R-squared: 0.5093, Adjusted R-squared: 0.5078
F-statistic: 339 on 19 and 6206 DF, p-value: < 2.2e-16The increasing gap at upper levels of grade is obvious but larger sample size is needed to achieve significance for all dummies.
NLSY97
N=1,524 blacks and 2,849 whites. The NLSY97 uses the ASVAB. I use the NLS custom weights by specifying respondents being in all of the selected years. Since race, ASVAB, grade, correspond to different survey years (1997, 1999, 2011), I selected those 3 years in the custom weight.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.25929 0.05768 -21.833 < 2e-16 ***
bw 0.72886 0.06454 11.293 < 2e-16 ***
educd1 -0.63269 0.52724 -1.200 0.23020
educd2 -0.50375 0.15875 -3.173 0.00152 **
educd3 -0.32750 0.09982 -3.281 0.00104 **
educd4 -0.17922 0.12006 -1.493 0.13558
educd6 0.42723 0.10623 4.022 5.87e-05 ***
educd7 0.59306 0.08732 6.792 1.25e-11 ***
educd8 0.80846 0.10759 7.514 6.89e-14 ***
educd9 1.09566 0.11350 9.653 < 2e-16 ***
educd10 1.55318 0.16029 9.690 < 2e-16 ***
bweducd1 -0.58385 0.67277 -0.868 0.38554
bweducd2 -0.18238 0.18109 -1.007 0.31394
bweducd3 -0.01114 0.11742 -0.095 0.92439
bweducd4 -0.02901 0.14004 -0.207 0.83589
bweducd6 -0.07778 0.11979 -0.649 0.51617
bweducd7 0.06220 0.09779 0.636 0.52476
bweducd8 0.26898 0.11556 2.328 0.01997 *
bweducd9 0.05308 0.12169 0.436 0.66273
bweducd10 -0.14189 0.17103 -0.830 0.40678
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 442.9 on 4353 degrees of freedom
Multiple R-squared: 0.4258, Adjusted R-squared: 0.4233
F-statistic: 169.9 on 19 and 4353 DF, p-value: < 2.2e-16The pattern is not obvious here and perhaps there is no group interaction, regardless of significance levels.
Need A Better Explanation
Someone who is arguing that IQ tests are biased must face the hard facts. Cultural theories must explain why the gap increases with education levels. They predicted that the black IQ would have lower heritability because heritability would decrease at lower socioeconomic levels. The reality is that blacks do not have lower heritability than whites (Pesta et al. 2020).
However even among hereditarians, this outcome has not been discussed thoroughly. Jensen (1973, p. 119) once argued this could be best explained in terms of black-white differential regression to the mean. That is, the offspring of black and white parents matched for IQ would differ in IQ.
Surely, one could say that education only captures a portion of the environmental factors which could potentially and differentially affecting blacks and whites. As explained before, adding more variables may instead obscure the genetic and environmental factors as opposed to a simpler model. More importantly, there is a good reason for using education instead of a more broadly defined SES variable which would typically include income.
There are several disadvantages with this variable. Income varies greatly with economic cycles, and any study conducted during the economic bust may have undesirable effects on blacks’ estimates of income because poor households are more negatively affected by economic shocks. Averaging across years to increase reliability is not always possible (e.g., GSS). The predictive power of income depends on the age of the infant at which the adult’s income has been measured (Muller, 2008, 2010). According to some, if not many, blacks are facing discrimination in the job market, leading to even lower income than whites.
Education has always been the main argument that blacks could catch up. The social mobility argument. One would wonder however if education truly increases intelligence.