What is behind the Flynn effect ?

The phenomenon known as secular IQ gains, or Lynn-Flynn Effect, is widely discussed. Extensive research has been done. Many theories have been proposed, such as nutrition, education, societal changes, for the most popular ones. Less commonly invoked are the genotype-environment correlation hypothesis, the heterosis, the life history model, the cultural bias, the rule-dependence model, or the assumption that the IQ test does not measure intelligence. It is even believed that Flynn gain is related to the black-white gap changes. None of the hypotheses advanced so far succeed to approach the “significance” of the Lynn-Flynn effect. There is, however, one conclusion that seems reasonable. The Flynn effect is not a Jensen effect. Intelligence has not increased.

1. The generality of the Flynn Effect.

According to Flynn (1987) review of secular gains in 14 (developed) countries, culture-reduced tests such as the Raven average 0.588 rate of gains and verbal tests average 0.374 rate of gains. In the US, children aged 2-18 gained 12 points between 1932-1972 whereas adults aged 16-75 gained 5.95 points between 1954-1978, the IQ rate gain per year being 0.300 and 0.243, respectively. Lynn (2013) provides only modest evidence of declining IQ gains over age (children to adolescence) in developed countries. Some studies show this pattern, others don’t.

But a quite different pattern may be suspected in developing countries. In Saudi Arabia, between 1977 to 2010, there is a pattern of declining Flynn gains among 8-15 years old children at each subsequent age (Batterjee et al., 2013). The same pattern of declining FE gains with age is seen in Darfur (Sudan) among 1006 children aged 9-18 years-old who were given the SPM (Khaleefa et al., 2010).

There seems to be no moderator regarding the Flynn gains. As Flynn (1987) noted, the FE gains occur among the very bright children, those qualified as gifted. The same pattern was discovered by Wai & Putallaz (2011) for the top 5% in SAT and ACT scores between 1981 and 2010. Flynn (1987, 2009) also noted that the IQ gains occur along the entire IQ distribution, whereas Lynn (2009a) shows several IQ studies evidencing larger gains at lower IQ levels.

The FE gains seem to have stopped (Williams, 2013, pp. 2-3) in developed countries and they even sometimes showed a reversal in some European countries, including Britain, Finland, Norway, Denmark, Sweden, Netherlands (Dutton & Lynn, 2013). It is not yet clear why FE gains have been slowed down or reversed during the 1970s-2000s in these countries.

Now, what about the non-normal populations ? Obviously, fewer samples are available, and thus fewer studies have been conducted. Still, they are some. For example, Lanfranchi & Carretti (2012, Figure 2) summarize studies on FE gains among children with Down Syndrome (DS). There is no obvious IQ gain among those children as pictured when the IQ is plotted against year of birth (ranging from 1955 to 2005) although the correlation was 0.164. On the other hand, the deaf children in Saudi Arabia has experienced a secular gain in the CPM of 0.306 IQ points per year among 10-12 years from 1999 to 2013 (Bakhiet et al., 2014), which is close to the SPM gain of 0.355 IQ points per year in the same country from 1977 to 2010 among 8-15 years old children although the IQ gains decrease substantially at each subsequent age (Batterjee et al., 2013). It is well known that deaf children show a large deficit in scholastic achievement and verbal IQ, as compared with normal-hearing children, whereas they don’t show any deficit in nonverbal IQ at all (Braden, 1994). Thus, their environmental disadvantages did not prevent them to show similar IQ gains in fluid tests with the normal population.

At the same time IQs were rising, achievement test scores, e.g., SAT, do not show any improvement at all, but instead a decline (Jensen, 1998, p. 322; Williams, 2013, p. 4). Flynn (1987) seems not to understand why both went different directions even though they are highly correlated. Rodgers (1999) responded that means and correlations are not necessarily related. This is because correlations deal only with rank-ordering. And if the mean changes impact every individual about equally, then the score rank-ordering among individuals may not change, leaving the correlation unchanged. An illustration is given here.

Other achievement tests, such the NAEP, show a rate of gains (Rindermann & Thompson, 2013) that is much lower, 1 “IQ” point per decade, than IQ tests.

2. The proposed hypotheses.

1 ) Psychometric IQ test does not measure intelligence.

The way we usually hear this argument, generally from the average person completely ignorant (and willing to remain ignorant) about psychometrics, the argument seems to be an ad hoc, for which someone is tempted to rely on when all other explanations fail badly. If it is not supposed to be a scientific argument, but instead a mere handwaving move, it needs not to be considered even further.

But Flynn (1987) is obviously more elaborate than this. He believes impossible such huge gains along the entire IQ distribution, occurring even among the very bright children, in the face of the absence of a cultural renaissance that should have taken place but which in fact did not, he concludes that IQ test measures a correlate of intelligence with no causal link to intelligence.

The current generation in the Netherlands must radically outperform the last or the Ravens test does not measure intelligence. Table 18 shows the effect of a 20-point gain on high IQ levels as measured in terms of 1952 norms. The same effect has probably occurred in France in that French gains, although tentative, are almost certainly as high as 15 or 20 points. These effects should be highly visible: 25% of the children teachers face qualify as gifted; those with IQs of 150 and above have increased by a factor of almost 60, which means that the Netherlands alone has over 300,000 people who qualify as potential geniuses. The result should be a cultural renaissance too great to be overlooked.

... Imagine that we could not directly measure the population of cities but had to take aerial photographs, which gave a pretty good estimate of area. In 1952, ranking the major cities of New Zealand by area correlated almost perfectly with ranking them by population, and in 1982, the same was true. Yet anyone who found that the area of cities had doubled between 1952 and 1982 would go far astray by assuming that the population had doubled. The causal link between population and its correlate is too weak, thanks to other factors that intervene, such as central city decay, affluent creation of suburbs, and more private transport, all of which can expand the city’s area without the help of increased population.

Clearly much the same is true of the Ravens and intelligence. The Ravens test measures a correlate of intelligence that ranks people sensibly for both 1952 and 1982, but whose causal link is too weak to rank generations over time. This poses an important question: If a test cannot rank generations because of the cultural distance they travel over a few years, can it rank races or groups separated by a similar cultural distance? The problem is not that the Ravens measures a correlate rather than intelligence itself, rather it is their weak causal link. When measuring the real-world phenomenon we call a hot day, we use the height of a column of mercury in a thermometer as a correlate, but note that this correlate has a strong causal link that allows it to give sensible readings over time. A thermometer not only tells us the hottest day of 1952 and the hottest day of 1982, it also gives a sensible measure of whether the summer of 1952 was hotter than the summer of 1982.

As to whether other IQ tests measure intelligence, the best path to clarity is to go from an ideal evidential situation to the actual one. Imagine the following situation in at least one nation: For every culturally reduced test in existence, strong data show massive IQ gains, say at least 10 points in a single generation; for every other IQ test in existence, a strong collective pattern of data shows that gains on them were less than massive only because of the inhibiting presence of learned content; that nation enjoyed no cultural renaissance in that generation. Then the conclusion that all IQ tests measure only a correlate of intelligence would be verified.

The theory offers no explanation as to why the scores always trended upward rather than in both directions. If Flynn is right, and that IQ does not measure intelligence, one would wonder why the Flynn effect correlates negatively with heritability and inbreeding depression whereas the g-loadings of the IQ subtests have an appreciable positive correlate with these indices of heritability. At the same time, the Flynn gains correlate positively with the vector of non-shared environments whereas the g-loadings show a large and consistent negative correlation (Hu, 2013). g-loadings, but not Flynn gains, correlate with heritability. It seems indeed that g and Flynn gains have different properties (Rushton, 1999). While this resolves one problem, it poses another. A negative correlation between IQ gains and g-loadings is only indicative that strengthening the g-loadedness of the tests will result in lower secular gains. If IQ tests are already very highly g-loaded, assuming g gains were inexistent, how is it possible to increase the g-loadedness of the tests so much as to make the IQ gains vanish ? One possibility is that test familiarity and other cultural factors cause the g-loadedness of the tests to decline (te Nijenhuis et al., 2007) thus accounting for the Flynn effect. If so, why measurement bias cannot account for either the totality or most of the Flynn gains, unless the current techniques do not allow us to fully detect cultural bias ? And why did the Flynn gains occur among the infants to the same extent as it has occurred among children (and perhaps adults) if the diminishing g-loadedness of cognitive tests was due to socio-cultural factors ? If no artifact is behind the Flynn gains, then the possibility of real IQ gains becomes more likely. As Flynn mentioned however, the impact on the society would have been visible. The absence of predictive validity excludes the possibility of g gain. And if the gains were concentrated only on narrow abilities, even in this case the social consequences must have been visible, since non-g abilities predict narrow domains of knowledge (Reeve, 2004) and narrow abilities (Coyle et al., 2013) and GPA (Coyle & Pillow, 2008) and job performance (Lang et al., 2010). This is especially true if modernization puts more weight on ability specification, in accordance with the declining test g-loadedness, as predicted by the life history model.

It seems impossible to break through this dilemma. There is, however, one way to circumnavigate around this problem. As Jensen (1998, p. 334) made it clear, g gains must translate into far transfer effects. Therefore, the best, and direct test of the hypothesis of no g gains is the examination of transfer effect.

If psychometric tests show the Flynn gain, it may be expected that chronometric tests will not. According to Jensen (1998, 2006) RT/IT measure is supposed to reflect the neurophysiological efficiency of the brain’s capacity to process information accurately. Indeed, it was found that while IQ tests improved with the generations, the reaction time tests show no improvement at all (Nettelbeck & Wilson, 2004; Dodonova & Dodonov, 2013). Now we need to ask the good questions. Both psychometric and chronometric tests are heritable. But is it really the case that a highly heritable trait cannot show large (environmentally-induced) improvement over time ? Lynn (2009a) acknowledged that height has also experienced a large secular gain, and yet there is no debate about the large heritability of height (Yang et al., 2010) at least as high as IQ. Still, no one would suggest that the measures of height are biased or do not measure height. However, with regard to IQ, the mere fact that chronometric tests show no gain may reinforce the hypothesis that psychometric tests do not measure what they were intended to measure.

When commenting on the Flynn effect, Jensen (2011) answered that such a phenomenon was not surprising, as IQ tests lack ratio scales. However, he wrongly attributed the IQ gains to test familiarity. Still, Jensen (1998, p. 206, 2006, p. 57) believed RT has some advantages over psychometric tests, as he writes that time itself is the natural scale of measurement for the study of information processes, to measure individual differences in the speed or efficiency of these information processes. Time is measured on an absolute, or ratio, scale with international standard units. Psychometric tests, however, are based on the number of items answered correctly on a particular test and therefore must be interpreted in relation to the corresponding performance in some defined normative population or reference group.

2 ) Nutrition and other biologically-related environments.

Lynn (2009a, pp. 18-19) shows that, among infants, the IQ (or DQ) gains per decade average about 3 points, or 0.30 per year, that is, more or less comparable to the rate gain of children and adults. In light of this findings, he argues :

The most straightforward explanation for the same rates of gain of the DQs of infants, the IQs of preschool children, and the IQs of older children and adults is that the same factor or factors have been responsible for both.

Consequently, Lynn rejects any significant role for education, or test-taking strategy. The social multipliers theory of Dickens and Flynn is also rejected because it would have predicted small gains among infants and preschool children, with gains progressively going up to adulthood due to cumulative effects, which did not occur. According to Lynn, the most plausible factor originates from a common cause, which could be an improvement in nutrition, among other factors having durable, sustainable impact.

Several researchers believe that the secular trends in height increases (an indicator of good health and nutrition) should have imitated the secular trends in IQ increases. In Norway, the height gains are concentrated toward the upper (height) distribution and FE gains toward the lower (IQ) distribution (Sundet et al., 2004, Figure 4), and the FE gains are not correlated with height gains, in Sweden (Rönnlund et al., 2013, p. 23). Flynn (2009) also believed the same, and used the argument that the timing of height gains don’t systematically coincide with the timing of IQ gains. These hasty conclusions however are unjustified, as Lynn (2009a) pointed out, nutritional effect is more complicated than a mere height gain.

Thus, the nutrition theory does not require perfect correlation between height and IQ changes, as Lynn maintained “the nutrition theory of the secular increase of intelligence does not require perfect synchrony between increases in height and intelligence. There appear to be some micronutrients the lack of which does not adversely affect height but adversely affects the development of the brain and intelligence”. Furthermore, Lynn (2009a) believes that the nutrition theory can easily explain why fluid IQ increased more than crystallized IQ because “Several studies have shown that sub-optimal nutrition impairs fluid intelligence more than crystallized intelligence (e.g. Lundgren et al., 2003), while nutritional supplements given to children raise their fluid IQs more than their crystallized IQs (Benton, 2001; Lynn & Harland, 1998; Schoenthaller, Bier, Young, Nichols, & Jansenns, 2000).” (p. 21).

So, if Lynn believes fluid IQ will improve more among poorer people, we must expect poorer countries showing better fluid IQ gains. Flynn & Rossi-Casé (2012) present the Raven’s gain in Argentina for adults. The gain was greater below the median (Table 4). The IQ gain per year was 0.814, and this is higher than the average gain (0.691) among the adults in other developed countries who took the Raven (Table 5a). In comparison, the average Raven’s gain in developed countries for children is 0.324 per year, and 0.628 for Argentina (Table 5b). At the same time, there were 3 samples in under-developed countries, Kenya, Dominica, Saudi Arabia, for which the Raven’s gains were, respectively, 1.000, 0.514, 0.355. Only Dominica has adult samples. There is yet no proof that the IQ gain is greater among poor countries.

In any case, it is not even certain that fluid IQ is the best approximate of g. Ashton & Lee (2006) demonstrate however that both Gc and Gf are (almost) equally important at indexing g, thus no evidence is provided that Gf is the best measure of g. The very fact that groups of children differing in mother’s education and family income as well as urbanization do not differ in FE gain rates in longitudinal data attenuates somewhat the nutrition theory (Ang et al., 2010). Indeed, if the nutrition hypothesis assumes larger IQ gains at low levels of IQ, then, a trend towards decreasing environmental variance must occur following the expected greater impact of nutritional gains over time among low IQ or low SES levels. Such a phenomenon results in lower variation due to environments. Thus, genetic variation must rise in response. Because no evidence of heritability decrease over time has been observed in the literature (e.g., Jensen, 1998, p. 328), it can be inferred that nutrition is not a plausible explanation. Mingroni (2007) advanced the same argument.

Flynn (2009) affirms that nutritional effects can be attributed to shared environmental factors, and since shared family effects vanish in adulthood, according to studies of IQ heritability, it renders nutritional theories unlikely. Nonetheless, those studies are confined to samples of mostly well nourished children. Thus, the vanishing effect of nutrition is not necessarily expected among the severely under-nourished children, but it still attenuates the hypothesis. Other biologically-related environments that include prenatal effects are likely to go under similar difficulties. As noted by Chuck (2012) and earlier by Herrnstein & Murray (1994) such prenatal effects would affect children in a way that is not reversible after birth. If prenatal effect is mainly a between-family effect and if shared environment indeed decreases with age as usually found in genetic studies conducted in developed countries, the argument is simply not compelling in the face of evidence of Flynn gains among adults.

Additionally, Flynn (2009) noted that, in Britain, Raven’s CPM gains were larger for high-SES children (at all age categories between 5 and 11) in the period of 1938-2008. Nonetheless, Raven’s SPM gains show no clear-cut pattern, because gains were larger among high-SES children of 5-9 years-old but became weaker than low-SES children 9-15 years-old. This does not square well with the nutrition history. Indeed, Flynn (2009) argues that the relatively larger gains induced by nutritional effects would show up in a reduction in IQ variance, as the bottom scores come closer to the top scores. In several countries, e.g., Argentina, Belgium, Canada, Estonia, New Zealand, Sweden, no evidence of SD reduction was found. Lynn (2009b) reported numerous cases where the Flynn gains were stronger among low IQ individuals. Perhaps the absence of variance reduction at the low IQ and SES levels in those countries is explained by additional factors impacting the middle- and high-levels of IQ. It is plausible that higher educated mothers provide an additional mothering effect to their children, that increased scores at low IQ levels have been counter-balanced by some obesity epidemic, either of these phenomena hiding the expected larger effect among low levels of IQ. If so, the meager proof of an absence of variance reduction at the lower IQ end is not a definitive refutation of the nutritional hypothesis. Nonetheless, Flynn’s skepticism about the nutrition hypothesis is justified by the findings that Flynn gains correlate negatively with indices of heritability, but correlates positively with non-shared environment, while showing a null correlation with shared environment (Hu, 2013). But worse comes from Sundet et al. (2010) who found the Flynn gains occurring within-families in Norway between cohorts 1950-1956, 1960-1965 and 1976-1983. Considering that nutrition is essentially a between-family factor, it must be rejected.

Another dramatic finding is that Draw-a-Person and Raven CPM show no gain in Brazil between 1980 and 2000 (Bandeira et al., 2012) among children aged 6-12, despite increases in nutrition and general health indices. Either the nutrition hypothesis is wrong or that other factors have entirely concealed the effect of nutrition on IQ gains. Then, what happened in Brazil ?

If the nutrition hypothesis implicates genuine gains, it encounters a problem. As Flynn (1987) explained, IQ gain has no predictive validity owing to the absence of cultural renaissance. The absence of g-loadedness regarding biologically-relevant environments has been confirmed by MCV meta-analyses (Metzen, 2012) although the method employed is sub-optimal for testing Spearman’s effect. Thus, either the nutritional gain is hollow with respect to g, or the IQ tests do not really measure what they are supposed to measure. The only way the nutrition hypothesis can account for the lack of predictive validity and hollow g in the Flynn gains is to assume that the nutrition gain among low-IQ levels is real (caused by nutrition) but is unreal (caused by test artifacts) among high-IQ levels. How could this be ?

3 ) Genetic factors.

Few genetic hypotheses have been proposed, certainly due to the fact that the gains were going too fast for genetic effects to capture those gains. Nonetheless, some have proposed heterosis as a (major) cause of Flynn gains (Jensen, 1998, p. 327; Mingroni, 2004, 2007). One problem is that Flynn gains don’t correlate either with subtest heritability or inbreeding depression whereas they correlate only with non-shared environment (Rushton, 1999; Hu, 2013). If heterosis implicates between but not within-family Flynn gains, then Sundet et al. (2010) findings of Flynn gain within sibship runs against the theory. As Woodley (2011b) mentioned, Mingroni’s simulation predicts a mere 2-3 points due to heterosis which is far from the 27-point gains in the USA over 80 years or so. Woodley also argues :

Another theoretical objection to the model concerns the idea that heterosis would actually lead to increases in IQ in all instances. Although it is likely that it would in instances where inbreeding is a relatively novel constraint on populations, there is no reason why it should in populations where inbreeding has been practiced constantly for many generations and where there has been an opportunity for purifying selection to purge the worst allele combinations.

4 ) Schooling and other societal changes.

As explained above, unless schooling can have an impact among infants, or that the causes in IQ increases among infants and children as well as adults are different and shift with age, with nutritional effects vanishing, and being replaced by educational gains, there is no hope for the theory.

The IRT test of Pietschnig et al. (2013, Table 3) showed that higher education moderates somewhat the secular gains, with d=0.24 and d=0.11 for latent gains uncorrected and corrected for education, between the 1978-81 and 1990-94 cohorts. The study sample was from Austria and the IQ battery is the Multiple-Choice Vocabulary Test (MWT-B). These gains were due to an improvement in the lower end of the IQ distribution, “Rather, a considerable part appears to be due to changes of the shape of the ability distribution: a decrease of performance variability was clearly observable in our IRT-based analyses, regardless of whether highest educational qualification was controlled for or not”, thus vindicating Rodger’s hypothesis. In any case, the apparent modest role for education needs not be causational, as the possibility of a hidden factor correlated with education and causing secular gains remains open.

If one wants to explain Flynn gains by educational gains, considering the stronger fluid gains, one would have to explain why education had brought about a greater fluid gain than crystallized gain despite the fact that Gc is more culturally loaded (in terms of scholastic component) than Gf. Jensen (1998, p. 325) argues that one by-product of schooling is an increased ability to decontextualize problems. That does not explain why Gf gain is so much greater than Gc. Even if we accept the argument, the investment theory would have predicted that higher Gf would, in turn, cause a greater Gc, because the more intelligent persons acquire knowledge faster (Jensen, 1998, p. 123).

More importantly, we need to distinguish between IQ gains due to real gains in intelligence and IQ gains due to knowledge gains. It is hard (if not impossible) to conceive an educational gain that does not incorporate knowledge gain. The consequence of this is that educational gain causes measurement bias. If school-related knowledge is elicited (at least some portion) by the IQ test, a disadvantaged group of people who do not have the required knowledge to get the items correct will fail these items even if they have equal latent ability with the advantaged group. This inevitably causes the meaning of group differences to be ambiguous (Lubke et al. 2003, pp. 552-553). In situations of unequal exposure, the test may be a measure of learning ability (intelligence) for some and opportunity to learn for others (Shepard, 1987, p. 213).

Considering that educational programs fail to sustain durable IQ gains, that education shows no transfer effect (Ritchie et al., 2013), and that educational deficits seem to be domain-specific among deaf children who lost only verbal IQ points but not nonverbal IQ points (Braden, 1994), there is no possible salvation for the schooling hypothesis. In general, the relevance of the schooling hypothesis depends on the assumption that the Flynn gains are actually intelligence gains.

But this is not the end. For instance, Wicherts (2007) believed that a violation in measurement equivalence with respect to cohorts among developed countries is not necessarily the expected pattern to be found in developed (poor) countries because the mechanisms at work under the Flynn effect are unlikely to be the same as the mechanisms at work in developed countries. For example, improved nutrition and societal changes (including school and urbanization) may be the leading causes behind FE gains in under-developed countries whereas in well-developed countries the leading causes were mass media exposure and other cultural changes, habits, and perhaps increases in environmental complexity bolstering higher cognitive load. But even if measurement bias does not account for Flynn gains in poor countries, this is not in itself proof that g gains had occurred.

Flynn effect has been found, indeed, in poor countries, such as South Africa (te Nijenhuis et al., 2011) although the Flynn gains for Indians (1.57 points per decade) were much lower than those for whites (3.63 or 2.85 points per decade). The white gain in South Africa is more or less similar with what is reported in developed countries. Nonverbal IQs increase more than verbal IQs, consistent with the literature. The authors reported that 22% of whites against 4.6% of non-whites attended school (private or public) in 1921. However, in 2007, the numbers were 76% for non-whites and 73% for whites. There was a tendency for the education gap to be closing between whites and non-whites but this has not prevented whites to have more IQ gains than non-whites. Nonetheless, the authors noted : “A special feature of the present paper is a comparison of test scores of Afrikaans- and English-speakers, starting with people born in 1896 and ending with people born in 1977. Over the course of approximately a century the large difference of about one SD in favor of English speakers diminishes by about three quarters. So, the group as a whole has a clear Flynn effect, but the effect is larger for the Afrikaans-speaking group. One could speculate that the diminishing gap between the Afrikaans- and English-speaking South Africans is driven partly by education and the diminishing gap in GDP between the two groups”.

The fatal blow comes from a study showing that the secular gain occurred between siblings (Sundet et al., 2010). Environmental factors which vary essentially between families, but not within, include home, education, nutrition, etc., do not explain such results.

5 ) Social multipliers and other G-E correlational models.

The model has been proposed by Dickens & Flynn (2001, pp. 347-349), for which the main assumption was that genetically advantaged people in a particular trait will become matched with superior environments for that trait. This is why Dickens (2005, p. 64) argue that “we might expect that persistent environmental differences between blacks and whites, as well as between generations, could cause a positive correlation between test score heritabilities and test differences” because their model implies that the more is the initial (physical) advantage and the more is the environmental influence on that trait. The theory implies that even minor differences in inherited abilities (e.g., talent, intelligence, …) could develop into major differences through social or environmental multipliers. The rationale goes like this : if a person was initially genetically advantaged in athletics, this person will have an inclination for sport practices. He will be motivated by the sort of tasks he performs well, which allows him to maximize his genetic potential, and thus his later performance, and this in turn gives him even more motivation. The better he gets, the more he enjoys the activity. This positive feedback is supposed to be the explanation of the increase in intra- and inter-group differences. Another important detail, as they note, “it is not only people’s phenotypic IQ that influences their environment, but also the IQs of others with whom they come into contact” (p. 347).

There is yet no compelling proof that Flynn gains are general intelligence gains given the absence of predictive validity. If Dickens & Flynn (2001) model of social multipliers implicates genuine gains, then the model is fragile to this violation.

The fact that score differences between cohorts are hollow with respect to g, as implied by reaction times, has some serious consequences for Dickens and Flynn (2001) model which has been extensively discussed (Loehlin, 2002; Rowe & Rodgers, 2002; Mingroni, 2007; Dickens & Flynn, 2002, Dickens, 2009).

Research on GCTA heritability demonstrates that the non-trivial IQ heritability (lower-bound estimates of about 0.40-0.50 for adults and 0.30-0.40 for children) cannot be due to genotype-environment correlation, even of active type, as the Dickens-Flynn model implies. Scarr & McCartney (1983) made it clear that the active rGE effect is the strongest among the more genetically related individuals, such as MZ twins, and the lowest among unrelated individuals, such as adopted siblings. Because GWA studies sample only unrelated individuals, we must understand that any rGE effect whatsoever plays virtually no role. This obviously weakens their model considerably, since it was based on the assumption that most of the genetic effect is driven by environmental effects.

The very fact that MCV analyses show negative correlation between subtest heritability and Flynn gain (Hu, Oct.5.2013) provide a definitive refutation of their model which has explicitly stated that the higher the heritability, the larger the environmental malleability and, thus, secular IQ gains. The Flynn gain was only correlated with non-shared environments. One curiosity was that Rushton (1999) study already offered evidence against their theory even before it came to them. Since inbreeding depression, an heritability index, does not correlate with Flynn gain, there is no credibility for the theory.

The fatal blow was given by Lynn (2009a). The equivalent gains among infants, children, adults, reject all theories based on environmental factors prevailing only after the infant stage, including social multiplier model (Dickens & Flynn, 2001) and mutualism model (van der Maas et al., 2006). Unless, of course, we assume that the nutrition gains among infants disappear, being progressively replaced by social-environment factors so as to result in equivalent gains for infants and children.

6 ) Hollow g and specific (narrow) abilities.

Indirect evidence is provided by Lynn (2009b) who reports that fluid IQ (Gf) increased in Britain between 1979 and 2008 whereas during approximately the same period, several verbal IQ (Gc) tests show no increase at all. If the IQ gain is confined to Gf, it must be domain-specific, and thus devoid of g.

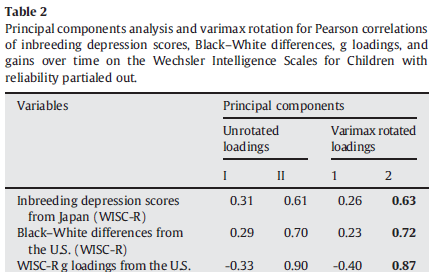
A more direct evidence comes from Rushton (1999, 2010) who conducted a principal component (PCA) and was able to show that IQ gains have their highest loadings on a different component than inbreeding depression, a pure genetic effect, and g-loadings and black-white differences who loaded on the same component (PC2) as shown below. In principle, PCA and factor analysis summarize the pattern of intercorrelation between the variables by assigning them to different clusters (PC or PF) according to how they correlate each other.

Then, Flynn (2000, pp. 202-214) provided a counterweight to Rushton’s analysis. Instead of using a measure of crystallized g (here, the WISC) he has created his measure of fluid-g loadings by correlating Raven’s test with each of the Wechsler subtest, since “Jensen (1998, p 38) asserts that when the g-loadings of tests within a battery are unknown, the correlation of Raven’s with each test is often used; and Raven’s is the universally recognized measure of fluid g.” (p. 207). What he found (Table 3) was a high loading on PC1 for black-white differences and fluid g and IQ gains, while inbreeding depression has its highest loading on a different component, PC2. Unfortunately, Flynn’s result is somewhat questionable. He removed one subtest, Mazes, from the analysis, with apparently no reason given. Because the Wechsler’s test is skewed towards a crystallized g, and that fluid-g loading is just the opposite side of crystallized-g loading in the Wechsler (Hu, Jul.5.2013), it is perhaps not surprising that he arrives at a different conclusion than Rushton’s. If different tests have different properties, a better test of Spearman effect must involve a correlation between g-loadings (complexity) and IQ gains within a given test, in order to control for test properties. In this case, both Rushton and Flynn were wrong. Moreover, Jensen (1998, pp. 90, 120) and Hu (Oct.5.2013) showed that the Raven correlated more with Wechsler’s crystallized tests than fluid tests, meaning that the rank ordering of (subtest) fluid g should mirror (subtest) crystallized g, which is not what we see in Flynn’s figures. The reason is due to the very low reliability of Flynn’s vector of g fluid. When adding more samples, it was found that Raven test tended to correlate more with crystallized subtests within the Wechsler. Also, Must et al. (2003, p. 470) who found no Jensen effect behind the secular gain in Estonia adds further comment on Flynn, saying that Gc and Gf dichotomy is unjustified, especially with regard to the fact that reaction times correlate with subtests g-loadings of the crystallized-biased ASVAB battery.

Actually, the correlations of subtest g-loadings with subtest gains show that the Flynn Effect is hollow with respect to g. Using Jensen’s method of correlated vectors (MCV), several studies have investigated the issue, yielding sometimes positive correlation (r) between g-loadings (g) and secular gains (d) but very often negative (or no) correlation. Dolan (2000; & Hamaker 2001) and others (Ashton & Lee, 2005) have criticized MCV. Jan te Nijenhuis (2007, pp. 287-288) countered by arguing that psychometric meta-analytic (PMA) methods, corrected for artifacts (e.g., sampling error, restriction of range of g loadings, reliability of the vector of score gains and the vector of g loadings, correction for deviation from perfect construct validity), could improve Jensen’s MCV, yielding more accurate results. The uncorrected (r) and corrected (p) correlations found were respectively -0.81 and -0.95, as shown in Table 2. The fact that those artifacts explained 99% of the variance in effect sizes means that other plausible moderators such as sample age, IQ-sample or test-retest interval, test type, play no role.

The large number of data points and the very large sample size indicate that we can have confidence in the outcomes of this meta-analysis. The estimated true correlation has a value of -.95 and 81% of the variance in the observed correlations is explained by artifactual errors. However, Hunter and Schmidt (1990) state that extreme outliers should be left out of the analyses, because they are most likely the result of errors in the data. They also argue that strong outliers artificially inflate the S.D. of effect sizes and thereby reduce the amount of variance that artifacts can explain. We chose to leave out three outliers – more than 4 S.D. below the average r and more than 8 S.D. below ρ – comprising 1% of the research participants.

This resulted in no changes in the value of the true correlation, a large decrease in the S.D. of ρ with 74%, and a large increase in the amount of variance explained in the observed correlations by artifacts by 22%. So, when the three outliers are excluded, artifacts explain virtually all of the variance in the observed correlations. Finally, a correction for deviation from perfect construct validity in g took place, using a conservative value of .90. This resulted in a value of -1.06 for the final estimated true correlation between g loadings and score gains. Applying several corrections in a meta-analysis may lead to correlations that are larger than 1.00 or -1.00, as is the case here. Percentages of variance accounted for by artifacts larger than 100% are also not uncommon in psychometric meta-analysis. They also do occur in other methods of statistical estimation (see Hunter & Schmidt, 1990, pp. 411-414 for a discussion).

Jan te Nijenhuis (2012; & van der Flier, 2013) replicated the study, and found null correlation in Dutch samples and negative correlations using Rushton (1999) & Flynn (2000) data.

In some instances, there had been a reversal of the Flynn effect (Dutton & Lynn, 2013). Interestingly, this anti-Flynn Effect could be correlated with g-loadings (Woodley & Meisenberg, 2013). Woodley and Madison (2013), using Must et al. (2009) estonian data, demonstrated that FE gains and changes in g-loadings (Δg) between measurement occasions displayed a robustly negative correlation. Again, this provides evidence that FE gains and general abilities are not related.

In general, the IQ batteries used are sometimes biased favorably toward crystallization. And it was sometimes argued that g has increased simply because the Raven, one of the most g-loaded tests available, showed the strongest IQ gains. This neglects the fact that different tests are confounded with test properties as well (see section 10).

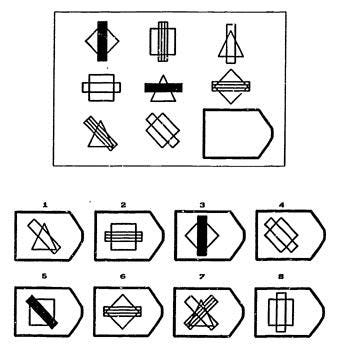
On the other hand, it is believed that Raven increases so much because people today indeed have been much more exposed to visual media and other visual experiences related to modernization of societies (Armstrong & Woodley, 2014). Such a phenomenon improves scores through test-content familiarity. Thus, under the effect of differential exposure to knowledge, it is not surprising that Raven’s gain scores show measurement bias as well, as demonstrated by Fox & Mitchum (2012). In sum, Raven’s gains exhibit DIF in the direction of either under- or over-estimation of scores in more recent cohorts. At equal total raw score, older cohorts would be less apt to map dissimilar objects but more apt to infer a greater number of rules. A description of what is a rule is shown below :

The correct answer is 5. The variations of the entries in the rows and columns of this problem can be explained by 3 rules.

1. Each row contains 3 shapes (triangle, square, diamond). 2. Each row has 3 bars (black, striped, clear). 3. The orientation of each bar is the same within a row, but varies from row to row (vertical, horizontal, diagonal).

From these 3 rules, the answer can be inferred (5).

Because there are 3 rules, the correct response must contain 3 correct objects. The authors classify the response categories as follows : 1 for no correct objects, 2 for one correct object, 3 for two correct objects, 4 for three correct objects. We see from their Figure 10, at any given Raven’s raw score, respondents having higher response categories are more likely to be members of older cohorts. Complexity in the Raven is a function of number and type of rules but also in the ability to map dissimilar rather than similar objects (Carpenter et al., 1990; Primi, 2001). Their analysis shows that Raven gain is confined to only one type of ability (mapping dissimilar objects) among the two major abilities elicited by the Raven. Thus, no evidence of g gain.

The very fact that Piaget tests, another very culture-free tests, display large secular IQ decline (Shayer et al., 2007, 2009) casts doubt on the argument that FE gains on culture-free tests (e.g., Raven) accredit the views that g has increased but also on the likelihood that Flynn gains have any transfer effects. Even Raven’s formidable gain is not observed everywhere. For instance, Raven’s gain was totally absent in Australia, between 1975 and 2003 (Cotton et al., 2005), and in Brazil, between 1980 and 2000 (Bandeira et al., 2012).

Most research on the Spearman-Jensen effect (i.e., g-loading correlates) are deceptive, however. At first glance, MCV and PCA tests reveal that the IQ gain is hollow, not real. Jensen (1998, p. 92) noted long ago that every IQ test measures g, but some tests measure g much better than others. Cognitive tests are all ranked onto a continuum of g-loadings. A negative correlation between g and IQ gain only means that the IQ gains will diminish as the g-loadedness of the tests increases. As Rushton & Jensen (2010) noted, g-loadedness declines with the amount of test familiarity. But as pointed out above, the infant gains exclude such artifacts in accounting for the g-loading declines over time. Furthermore, if FE gains diminish with the amount of test g-loadedness, in no way these analyses prove that FE gains had not occurred. But it suggests at least that the IQ gains may not be transferable to non-trained IQ tests. Thus, the best way to test the said hypothesis is to examine an IQ test that is trainable and another that is not or hardly trainable, such as reaction time tests (Jensen, 2006).

By far the best study showing the absence of intelligence gains would be a study of reaction/inspection times across cohorts. There is one study that has investigated this issue. And this study (Nettelbeck & Wilson, 2004), although with small Ns, demonstrates the absence of FE gains in IT despite improvement in PPVT (a highly culture-loaded test). The author writes “Despite the Flynn effect for vocabulary achievement, Table 1 demonstrates that there was no evidence of improvement in IT from 1981 (overall M= 123±87 ms) to 2001 (M = 116±71 ms)”. The hollow gain underlying the Flynn Effect is further vindicated. Furthermore, Woodley et al. (2013) found evidence of slowering RT in Britain, between 1884 and 2004, corresponding to -1.23 IQ points per decade, or 14 points since Victorian times. The study relies much on Galton’s set of data (1889). But Jensen (1998, p. 23) informed us that Galton’s measure of RT had a reliability of only 0.18. Besides, their study has not been well received (Dodonova & Dodonov, 2013). These authors still report, however, that RT shows no particular trend, which is consistent with Nettelbeck & Wilson (2004) study that people are becoming smarter but not faster.

Now, the whole argumentation about g and Flynn gain has been debated. When Jensen (1973) argument was that given the known IQ heritability and the known black-white IQ difference, the hypothesis of purely environmental factors causing the black-white differences imply an SD difference in environments too large to be plausibly coherent with what is happening in the real world, Flynn (2010a, p. 364) applied this argument to the Flynn effect to counter Jensen :

Originally, Jensen argued: (1) the heritability of IQ within whites and probably within blacks was 0.80 and between-family factors accounted for only 0.12 of IQ variance — with only the latter relevant to group differences; (2) the square root of the percentage of variance explained gives the correlation between between-family environment and IQ, a correlation of about 0.33 (square root of 0.12=0.34); (3) if there is no genetic difference, blacks can be treated as a sample of the white population selected out by environmental inferiority; (4) enter regression to the mean — for blacks to be one SD below whites for IQ, they would have to be 3 SDs (3×.33=1) below the white mean for quality of environment; (5) no sane person can believe that — it means the average black cognitive environment is below the bottom 0.2% of white environments; (6) evading this dilemma entails positing a fantastic “factor X”, something that blights the environment of every black to the same degree (and thus does not reduce within-black heritability estimates), while being totally absent among whites (thus having no effect on within-white heritability estimates).

I used the Flynn Effect to break this steel chain of ideas: (1) the heritability of IQ both within the present and the last generations may well be 0.80 with factors relevant to group differences at 0.12; (2) the correlation between IQ and relevant environment is 0.33; (3) the present generation is analogous to a sample of the last selected out by a more enriched environment (a proposition I defend by denying a significant role to genetic enhancement); (4) enter regression to the mean — since the Dutch of 1982 scored 1.33 SDs higher than the Dutch of 1952 on Raven’s Progressive Matrices, the latter would have had to have a cognitive environment 4 SDs (4×0.33=1.33) below the average environment of the former; (5) either there was a factor X that separated the generations (which I too dismiss as fantastic) or something was wrong with Jensen’s case. When Dickens and Flynn developed their model, I knew what was wrong: it shows how heritability estimates can be as high as you please without robbing environment of its potency to create huge IQ gains over time.

The logic here is not correct because Flynn compares what are probably unreal IQ differences between cohorts while Jensen compares genuine g differences between racial groups. IQ gain has no predictive validity. IQ difference within and between groups at any given time has predictive validity. Flynn continues to deny g as a valid argument against the phenomenon of secular gains :

You cannot dismiss the score gains of one group on another merely because the reduction of the score gap by subtest has a negative correlation with the g loadings of those subtests. In the case of each and every subtest, one group has gained on another on tasks with high cognitive complexity. Imagine we ranked the tasks of basketball from easy to difficult: making lay-ups, foul shots, jump shots from within the circle, jump shots outside the circle, and so on. If a team gains on another in terms of all of these skills, it has closed the shooting gap between them, despite the fact that it may close gaps less the more difficult the skill. Indeed, when a worse performing group begins to gain on a better, their gains on less complex tasks will tend to be greater than their gains on the more complex. That is why black gains on whites have had a (mild) tendency to be greater on subtests with lower g loadings.

Reverting to group differences at a given time, does the fact that the performance gap is larger on more complex then easier tasks tell us anything about genes versus environment? Imagine that one group has better genes for height and reflex arc but suffers from a less rich basketball environment (less incentive, worse coaching, less play). The environmental disadvantage will expand the between-group performance gap as complexity rises, just as much as a genetic deficit would. I have not played basketball since high school. I can still make 9 out of 10 lay-ups but have fallen far behind on the more difficult shots. The skill gap between basketball “unchallenged” players and those still active will be more pronounced the more difficult the task. In sum, someone exposed to an inferior environment hits what I call a “complexity ceiling”. Clearly, the existence of this ceiling does not differentiate whether the phenotypic gap is due to genes or environment.

While Flynn was perfectly right that a low-g person would improve more on less g-loaded items (i.e., less complex) than on the more g-loaded items, his analogy is defectuous. As Chuck (Feb.17.2011) pointed out :

We could use a basketball analogy to capture both positions on this matter. Flynn argues that g is analogous to general basketball ability; it’s important because it correlates with the ability to do complex moves, say like making reverse two-handed dunks. Flynn’s point is that to do a reverse two-handed dunk, one needs to learn all the basic moves. Since environmental disadvantages (poor coaches, limited practicing space, etc.) handicap one when it comes to basic moves, they necessarily handicap one more when it comes to complex basketball moves. Rushton and Jensen argue the g is analogous to a highly heritable athletic quotient; it’s important because it correlates with basic physiology, generalized sports ability, and basic eye-motor coordination. Their point is that it’s implausible that disadvantages in basketball training would lead to across the board disadvantages in all athletic endeavors and, moreover, lead to a larger handicap in general athleticism than to a handicap in basic basketball ability. Rather than disadvantages in basketball training leading to disadvantages in general athletic ability, it’s much more plausible that disadvantages in general athletic ability would lead to a reduced effectiveness of basketball training.

Flynn and other environmentalists can only circumnavigate g by insisting that a web of g affecting environmental circumstances, in effect, constructs g from the outside in. Given that g is psychometrically structurally similar across populations, sexes, ages, and cultures this seems implausible as it would necessitate that either everyone happened to encounter the same pattern of g formative environmental circumstances just at different levels of intensity or that environmental circumstances were themselves intercorrelated.

The lack of practice in one domain will surely affect this single domain more than it affects abilities in all domains of sports. The reverse is true. Practice in one domain will affect this single domain more than all domains in sports. This is how Murray (2005, fn. 71) puts it :

An athletic analogy may be usefully pursued for understanding these results. Suppose you have a friend who is a much better athlete than you, possessing better depth perception, hand-eye coordination, strength, and agility. Both of you try high-jumping for the first time, and your friend beats you. You practice for two weeks; your friend doesn’t. You have another contest and you beat your friend. But if tomorrow you were both to go out together and try tennis for the first time, your friend would beat you, just as your friend would beat you in high-jumping if he practiced as much as you did.

This is best illustrated by Jensen (1998) who explained that a g-loaded effect should be generalizable, irrespective of g-loadings or task difficulty : “Scores based on vehicles that are superficially different though essentially similar to the specific skills trained in the treatment condition may show gains attributable to near transfer but fail to show any gain on vehicles that require far transfer, even though both the near and the far transfer tests are equally g-loaded in the untreated sample. Any true increase in the level of g connotes more than just narrow (or near) transfer of training; it necessarily implies far transfer.” (p. 334). As we have seen, the few studies on RT/IT measures seem to suggest that being smarter is not synonymous with being faster, thus nullifying Flynn argumentation. Nonetheless, Flynn criticism reveals that the studies based on MCV and other methods (PCA, MGCFA) are sub-optimal. What is most needed is a study evaluating directly the transfer effect of the Flynn gains. Most scientists have simply been wrong all along in focusing on psychometric tests rather than on chronometric tests.

7 ) Predictivity issues.

A criticism of the Flynn Effect (FE) that seems to have gone unnoticed by most researchers is from Jensen (1998, pp. 331-332). He argued that if the gains were real, the later time point (younger cohort) would show underprediction of IQ on a wide variety of criterion measures, relative to the earlier time (older cohort). In other words, when IQ is held constant, recent cohorts would outperform old cohorts on, say, achievement tests. This is how Jensen describes the situation :

A definitive test of Flynn’s hypothesis with respect to contemporary race differences in IQ is simply to compare the external validity of IQ in each racial group. The comparison must be based, not on the validity coefficient (i.e., the correlation between IQ scores and the criterion measure), but on the regression of the criterion measure (e.g., actual job performance) on the IQ scores. This method cannot, of course, be used to test the “reality” of the difference between the present and past generations. But if Flynn’s belief that the intergenerational gain in IQ scores is a purely psychometric effect that does not reflect a gain in functional ability, or g, is correct, we would predict that the external validity of the IQ scores, assessed by comparing the intercepts and regression coefficients from subject samples separated by a generation or more (but tested at the same age), would reveal that IQ is biased against subjects from the earlier generation. If the IQs had increased in the later generation without reflecting a corresponding increase in functional ability, the IQ would markedly underpredict the performance of the earlier generation – that is, their actual criterion performance would exceed the level of performance attained by those of the later generation who obtained the same IQ. The IQ scores would clearly be functioning differently in the two groups. This is the clearest indication of a biased test – in fact, the condition described here constitutes the very definition of predictive bias. If the test scores had the same meaning in both generations, then a given score (on average) should predict the same level of performance in both generations. If this is not the case (and it may well not be), the test is biased and does not permit valid comparisons of “real-life” ability levels across generations.

As Williams (2013) noted, “This assumes that the later test has not been renormed. In actual practice tests are periodically renormed so that the mean remains at 100. The result of this recentering is that the tests maintain their predictive validity, indicating that the FE gains are indeed hollow with respect to g”. But also because there is no predictive bias against blacks (i.e., underprediction), before or after correction for unreliability, Jensen concluded that the Flynn Effect (FE) and the B-W IQ gap must have different causes. In fact, a better illustration that the black-white IQ gap is not related with Flynn gains is provided by Ang et al. (2010) in a longitudinal study (CNLSY79) where it has been observed that racial groups did not differ in FE gain rates. A more definitive proof is given by the data showing the absence of B-W gap reduction over nearly 100 years during the 20th century (Fuerst, 2013).

Back to the argumentation of predictive bias with respect to cohort, it was found that MZ twin differences don’t correlate meaningfully with social outcomes (Nedelec et al., 2012). MZ differences correlate modestly with education (Beta= 0.142, 0.120) and negatively with income (Beta= -0.185, -0.207) which is to say, higher IQ predicts higher education but lower income. This is relevant because MZ difference would be purely a non-shared environmental effect. The inconclusive correlations may mean, despite the low sample size, that non-shared environment has no predictive value. If FE gains correlates so strongly with non-shared environment, this suggests (but does not prove) that the IQ gains have no predictive value, consistent with the view of hollow g gains.

As explained in Section 1, Flynn has provided the best evidence that the IQ gain is hollow. The only way this assumption can be violated is to posit that other confounding factors acted to entirely conceal the effect of IQ gains. At first glance, this is not implausible to the extent that the correlation between IQ and diverse social outcomes is far from being 100%. As Flynn made it clear, however, the IQ gain was just too much to be concealed so easily. This is rendered even more difficult if the claims by Herrnstein & Murray (1994) and Gottfredson (1997) about the increasing complexity of modern societies that put much more weight on cognitive abilities today than in the past were true because these external factors will probably increase IQ predictivity, rendering the effect of secular gains even more salient.

8 ) Cultural bias hypothesis.

Psychometric bias has several sources of causes, e.g., guessing, coaching, knowledge, attitude. When a test or a subtest or a test item is free of bias, the only factor that explains the scores must be the individuals’ ability. But if the scores also depend on the group (gender, race, cohort, age) to which the individuals belong, then the test measures a “nuisance” factor that was not intended to be measured by the test. As a result, when groups are equated on total score, they have different probabilities of answering the test item correctly, owing to relative differences with regard to external factors impacting test item scores.

One possible factor accounting for FE gains has been proposed by Brand (1987) who pointed out, “it is perhaps not surprising if they now record gains as education takes a less meticulous form in which speed and intelligent guessing receive encouragement in the classroom”. If the guessing effect is large, it must be detectable through IRT and MGCFA. As we will see, this hypothesis does not hold water. Jensen (1998) tells us that Brand has attempted to explain the higher gains in Raven compared to crystallized tests by the greater tendency among test-takers for guessing : “These tendencies increase the chances that one or two multiple-choice items, on average, could be gotten “right” more or less by sheer luck. Just one additional “right” answer on the Raven adds nearly three IQ points” (p. 323). The Raven seems very sensitive to external factors such as attitude in test-taking. However, Flynn (1987) noted that Raven’s gain accelerated in the Netherlands during the last decades of gains. Surely, guessing strategy would have quickly reached a point of saturation, thus slowing or stopping the IQ gains, not the reverse. Furthermore, in Britain, the Flynn gain on CPM was 0.187 and 0.382 points per year for the periods 1947-1982 and 1982-2007 and the gain on SPM was 0.256 and 0.320 points per year for the periods 1938-1979 and 1979-2008 (Flynn, 2009, Table 3).

Another factor is test sophistication, which may produce differences in test familiarity between members of different groups, e.g., cohorts. But Flynn (1987) seems to agree with Lynn regarding the weak role of test sophistication and education :

There is indirect evidence that test sophistication is not a major factor. It has its greatest impact on naive subjects, that is, repeated testing with parallel forms gives gains that total 5 or 6 points. It seems unlikely that a people exposed to comprehensive military testing from 1925 onward were totally naive in 1952. Moreover, test sophistication pays diminishing returns over time as saturation is approached, and as Table 1 shows, Dutch gains have actually accelerated, with the decade from 1972 to 1982 showing the greatest gains of all. Reviewing the factors discussed, higher levels of education contribute 1 point, SES may contribute 3 points, and what for test sophistication, perhaps 2 points? These estimates cannot simply be summed because the factors are confounded; for example, higher SES encourages staying in school longer, which raises test sophistication. Together they appear to account for about 5 points.

As we will see, the role of test content familiarity is minor, as shown by measurement bias studies, notably MGCFA and IRT. FE gains violate the so-called measurement invariance. This may happen if two groups differ in knowledge (exposure) relevant to the test, or differ in attitude in test taking (anxiety, guessing, etc.). Mingroni (2007, p. 812) illustrates as follows :

For example, Wicherts (personal communication, May 15, 2006) cited the case of a specific vocabulary test item, terminate, which became much easier over time relative to other items, causing measurement invariance to be less tenable between cohorts. The likely reason for this was that a popular movie, The Terminator, came out between the times when the two cohorts took the test. Because exposure to popular movie titles represents an aspect of the environment that should have a large nonshared component, one would expect that gains caused by this type of effect should show up within families. Although it might be difficult to find a data set suitable for the purpose, it would be interesting to try to identify specific test items that display Flynn effects within families. Such changes cannot be due to genetic factors like heterosis, and so a heterosis hypothesis would initially predict that measurement invariance should become more tenable after removal of items that display within-family trends. One could also look for items in which the heritability markedly increases or decreases over time. In the particular case cited above, one would also expect a breakdown in the heritability of the test item, as evidenced, for example, by a change in the probability of an individual answering correctly given his or her parents’ responses.

Because of such (cultural) influences, the older cohorts will be disadvantaged in some items, subtests. Obviously, the (inflated) score of the younger cohort may be partly or totally accounted for by cultural bias. In some instances, factorial invariance could be considered as a test of cultural bias.

To begin, one problem with test bias studies, especially MGCFA, is the claim that a presence of bias implies incomparability of scores (e.g., Wicherts, 2004; Must, 2009). This is just wrong. The scores are comparable. It is just that some subtests or items are (dis)advantaging one group against the other. The unbiased score is simply lower or higher than the uncorrected-for-bias score.

One technique in use is the Multi Group Confirmatory Factor Analysis (MGCFA) which is a sub-class of CFA/SEM analyses. The method compares a series of constrained models to an unconstrained (free) model. In each subsequent model, one constraint is added. The final step, fourth, must have 4 constraints. In the first step, the observed variables (subtests) must have a similar pattern of clustering and a similar number of observed variables per latent factor between the groups studied. This can be also examined by a rotated oblique factor analysis (e.g., promax). Specifically, if arithmetic and vocabulary subtests cluster together whereas coding and block design form another cluster in one group but that these same subtests cluster differently in the other group, then the scores in the subtests are not caused by the same latent ability across groups, and configural invariance is violated. In the second step, the group difference in the correlations (factor loadings) between subtests and first-order latent group factors is evaluated. When the difference is large, it is said that these subtests have different degrees of importance (within the first-order latent group factor they belong to) between the groups. Thus, non-uniform bias is detected and metric invariance is violated. In the third step, the mean score (intercept) of each observed variable (subtest) is held equal across groups, while allowing the latent factors to be freely estimated (i.e., not equated). If the mean scores in observed variables are different, the groups do not differ solely on their level of latent factor means but also on the specific subtest(s). Thus, uniform bias is detected and scalar invariance is rejected. In the fourth step, the residual variances (i.e., uniqueness or measurement error) are set to be equal across groups. If the percentage of uniquess/error differs across groups, then residual invariance is rejected. Each of these steps, or models, must be compared with the null model, which has no constraint, i.e., all parameters are freely estimated and thus not equated across groups. This is estimated by way of model fit, e.g., CFI, RMSEA, (S)RMR, ECVI. For measurement invariance to hold, generally, it is possible to disregard step 4th. In other words, if either the configural, metric or the scalar step shows lack of equivalence between groups, we are in the presence of psychometric bias. The second, third, and fourth step correspond to weak, strong, strict invariance. At least strong invariance must be reached.

It is even possible to test the invariance of the second-order latent g and at the same time the g model. To do this, one needs to hold constant (by fixing parameters to be equal) across groups the mean score of some of the first-order latent factors and g, if the weak version of Spearman’s Hypothesis is the focus of interest, as well as fixing the second-order factor’s correlation with the first-order latent factors and the residual variances of the first-order factors to be equal. In presence of fit decrement, the second-order g would fail to fully explain the difference in subtest score means across groups. The strong (weak) version of Spearman’s Hypothesis predicts that the source of the difference would be uniquely (mainly) due to differences in the second-order latent g. If the first-order latent factors account modestly for the difference, the weak (but not strong) version of SH is supported.

Anyway, in MGCFA framework, an observed score is not measurement invariant when two groups having the same latent ability (i.e., being identical on the construct(s) being measured) have different probabilities of attaining the same score on the subtest. Wicherts & Dolan (2010) explicitly stated that “mean group differences on the subtests should be collinear with the corresponding factor loading”. Wicherts et al. (2004) conducted such a study.

But their study is far from being satisfying. They establish that Flynn gains cannot be accounted for by (first-order) latent common factors on the grounds that the IQ subtests among diverse batteries are not fully equivalent between cohorts. This conclusion however can be justified only if subtest biases account (at least) for the majority of the Flynn gain. Thus, the subtest bias, which is better called Differential Bundle Functioning (DBF), when taken in combination must reveal a phenomenon called cumulative DBF. That is, the biases apparent in each subtest must be one-sided, systematically under-estimating the true ability of one specific group. If the biases run in both directions and nullify each other at the test level, it must be concluded that measurement bias accounts for zero percent of the Flynn gain. As Roznowski & Reith (1999) explained, bias and DIF/DBF are two different concepts and must not be confused. If the many DIF/DBF cancel out at the total test score level, then no test bias can be established. It makes no sense to talk about test bias if there is only subtest bias. Wicherts et al. (2004) did not always make explicit the direction of the bias at the subtest level.

They also claimed that the Flynn gains and the black-white IQ difference have different causes because the B-W difference is invariant (Dolan, 2000; Dolan & Hamaker, 2001; Lubke et al., 2003) whereas Flynn gain is not. Once again, this may be true only if the secular gain is attributed mainly to measurement bias. Unfortunately, they have not attempted to estimate the percentage of score gain that is solely due to measurement bias. Hopefully, a close reading of their 5 studies suggests that the IQ gain is not entirely attributed to psychometric bias. In each study, except the last one, only a few subtests had been the cause of the MGCFA model misfit. Thus, the poor explanatory power of bias to account for the entirety of the cohort difference is in accordance with Flynn (1987) expectation that test sophistication and familiarity do not play a significant role in the phenomenon, even though Flynn himself has shifted his mind later on.

Using MGCFA as well, on two cognitive tests, ACT (1990-2010) and EXPLORE (1995-2010), from the Duke TIP data, Wai & Putallaz (2011) come up with another rejection in measurement invariance for the secular gains on a very large sample size. Again, partial invariance reveals sufficient fit. Thus, cognitive gains were still present.

For example, for tests that are most g loaded such as the SAT, ACT, and EXPLORE composites, the gains should be lower than on individual subtests such as the SAT-M, ACT-M, and EXPLORE-M. This is precisely the pattern we have found within each set of measures and this suggests that the gain is likely not due as much to genuine increases in g, but perhaps is more likely on the specific knowledge content of the measures. Additionally, following Wicherts et al. (2004), we used multigroup confirmatory factor analysis (MGCFA) to further investigate whether the gains on the ACT and EXPLORE (the two measures with enough subtests for this analysis) were due to g or to other factors. 4

4. … Under this model the g gain on the ACT was estimated at 0.078 of the time 1 SD. This result was highly sensitive to model assumptions. Models that allowed g loadings and intercepts for math to change resulted in Flynn effect estimates ranging from zero to 0.30 of the time 1 SD. Models where the math intercept was allowed to change resulted in no gains on g. This indicates that g gain estimates are unreliable and depend heavily on assumptions about measurement invariance. However, all models tested consistently showed an ACT g variance increase of 30 to 40%. Flynn effect gains appeared more robust on the EXPLORE, with all model variations showing a g gain of at least 30% of the time 1 SD. The full scalar invariance model estimated a gain of 30% but showed poor fit. Freeing intercepts on reading and English as well as their residual covariance resulted in a model with very good fit: χ² (7) = 3024, RMSEA = 0.086, CFI = 0.985, BIC = 2,310,919, SRMR = 0.037. Estimates for g gains were quite large under this partial invariance model (50% of the time 1 SD). Contrary to the results from the ACT, all the EXPLORE models found a decrease in g variance of about 30%. This demonstrates that both the ACT and EXPLORE are not factorially invariant with respect to cohort … gains may still be due to g in part but due to the lack of full measurement invariance, exact estimates of changes in the g distribution depend heavily on complex partial measurement invariance assumptions that are difficult to test. Overall the EXPLORE showed stronger evidence of potential g gains than did the ACT.

The importance of knowing the direction of bias is best illustrated by Must et al. (2009). They use MGCFA to compare the structure of means and covariance between three cohorts (1933/36, 1997/98, and 2006) among Estonian schoolchildren who took the NIT test. As was the case with Wicherts, the misfit was detected at the intercept level. Here again, they have not estimated the percentage of gap accounted for by measurement bias, but they made very explicit the direction of the subtest bias :

Six NIT subtests have clearly different meaning in different periods. The fact that the subtest Information (B2) has got more difficult may signal the transition from a rural to an urban society. Agriculture, rural life, historical events and technical problems were common in the 1930s, such as items about the breed of cows or possibilities of using spiral springs, whereas at the beginning of the 21st century students have little systematic knowledge of pre-industrial society. The fact that tasks of finding synonyms–antonyms to words (A4) is easier in 2006 than in the 1930s may result from the fact that the modern mind sees new choices and alternatives in language and verbal expression. More clearly the influence of language changes was revealed in several problems related to fulfilling subtest A4 (Synonyms–Antonyms). In several cases contemporary people see more than one correct answer concerning content and similarities or differences between concepts. It is important that in his monograph Tork (1940) did not mention any problems with understanding the items. It seems that language and word connotations have changed over time.

The sharp improvement in employing symbol–number correspondence (A5) and symbol comparisons (B5) may signal the coming of the computer game era. The worse results in manual calculation (B1) may be the reflection of calculators coming in everyday use.

Besides, their Table 4 is particularly enlightening. The mean intercorrelation of NIT subtests shows a stark decline from the 1933 cohort to the 1997 or 2006 cohort. Furthermore, the difference in the g-factor loadings between the 1933 and 1997 (or 2006) cohort, as assessed using F-statistic, is significant (although significance tests should never be trusted due to their dependence on sample size). Both of these strongly suggest a decline in g, and thus the hollowness of FE gains in Estonia. In general, their account suggests that the subtest bias (DBF) may tend to cancel out at the test level. This has been confirmed by Shiu & Beaujean (2013, Table 3). They demonstrate, using Item Response Theory (IRT) modeling, that the unbiased score gain (IRT) by subtest is more or less comparable to the biased score gain (CTT). Again, bias cannot account for the Flynn gain. The subtests were unidimensional, thus IRT assumption was met. A large portion (1/3 to 1/2) of subtests’ items show DIF.

To introduce IRT, which is a latent variable modeling at the item level, the method tests the group equality of item discrimination (factor loading), item difficulty (intercepts) and item guessing, respectively, parameter a, b, c. Evidence of group difference in either one of these parameters reveals DIF, Differential Item Functioning, that is, the groups have different probabilities of answering the item(s) correctly when equated for test total (latent) score. They are of 3 types, uniform, non-uniform and crossing non-uniform DIF. The IRT estimates first the best fit among models with no parameters (the baseline), one, two, three parameters, precisely, (b) difficulty alone, difficulty with (a) discrimination, or difficulty with discrimination and (c) guessing parameters. Basically, a free model is compared to models with constrained parameters. But it can begin with a-parameter. When the free model is compared to the a-contrained model and that the a-parameter is measurement invariant, it means either there is uniform DIF or no DIF. Another constraint, b, is added and constrained-b model is compared to constrained-a model. The uniform DIF is revealed when b is not invariant, regardless of a. Also, non-uniform DIF can be revealed when a is not invariant, regardless of b. In other words, the model is fitted at each step, with one additional constraint at each step, exactly like MGCFA procedure. Each step corresponds to 1PL (Rasch model), 2PL, 3PL. Because IRT deals with latent variable(s), the impact of measurement error is somewhat attenuated.

A framework of IRT is the comparison with CTT with regard to assumption. Classical Test Theory (CTT) postulates that a test score can be decomposed into two parts, a true score and an error component. It is assumed that the error component is random with a mean of zero and is uncorrelated with true scores, and that the observed scores are linearly related to true scores and error components. But, Item Response Theory (IRT) postulates that the probability of correct responses to a set of questions is a function of true ability and of one or more parameters specific to each test question.

It seems, historically, that IRT was known as latent trait theory or, as Jensen was used to say, Item Characteristic Curve (ICC). Jensen (1980, p. 443 and following) gives the description of such analyses : “If the test scores measure a single ability throughout their full range, and if every item in the test measures this same ability, then we should expect that the probability of passing any single item in the test will be a simple increasing monotonic function of ability, as indicated by the total raw score on the test.” (p. 442). No measurement bias is detected if item equivalence holds, with parameters (a, b, c) of the ICC being invariant across groups. Here is Jensen’s explanation of the concept :

Hence, a reasonable statistical criterion for detecting a biased item is to test the null hypothesis of no difference between the ICCs of the major and minor groups. In test construction, the items that show a significant group difference in ICCs should be eliminated and new ICCs plotted for all the remaining items, based on the total raw scores after the biased items have been eliminated. The procedure can be reiterated until all the biased items have been eliminated. The essential rationale of this ICC criterion of item bias is that any persons showing the same ability as measured by the whole test should have the same probability of passing any given item that measures that ability, regardless of the person’s race, social class, sex, or any other background characteristics. In other words, the same proportions of persons from each group should pass any given item of the test, provided that the persons all earned the same total score on the test. In comparing the ICCs of groups that differ in overall mean score on the test, it is more accurate to plot the proportion of each group passing the item as a function of estimated true scores within each group (rather than raw scores on the test), to minimize group differences in the ICCs due solely to errors of measurement.

Using the IRT technique, Beaujean & Osterlind (2008) analyzed the PPVT-R (1990-2004) and PIAT-math (1996-2004) in the CNLSY79 sample. Since IRT requires the test to be unidimensional (measuring one and only one ability) they have to meet the assumption, which was supported. Then, the constrained models were compared and it was found that 2PL fitted the data best, i.e., the guessing parameter was not an important factor behind the Flynn effect. As a result, c-parameter was constrained to zero whereas a- and b-parameters are freely estimated. Any items not exhibiting DIF were used as equating (anchor) items, and the two forms of the test (using all items) were equated, again. This allows the estimated latent trait (θ) scores to be directly comparable across groups. In PPVT-R, the raw, standard score, percentile, and IRT score gains were 0.17, 0.27, 0.27, 0.13 SD per year. In PIAT-math, the raw, standard score, percentile, and IRT score gains were 0.13, 0.41, 0.48, 0.06 SD per year. Since the score gains have almost vanished only in PIAT-math, they provide meager evidence of the role of test bias in accounting for FE gains.

Later on, Must (2013, pp. 7-9) also found in Estonia that changes in test-taking strategies were involved behind the Flynn Effect. The decline in missing answers was accompanied by a rise in wrong and correct answers. This suggests that the role of guessing in completion of tests has become more important over time.

In the period 1933/36-2006 mean subtest results of comparable age-cohorts have changed (Table 2). There is a general pattern that the frequency of missing answers in NIT subtests is diminished (approximately 1 d), with the exception of the subtest B1 (Computation), where the rise in missing answers was 0.36 d. The rise of right answers is evident in most of the subtests (7 from 9). The mean rise of right answers per subtest is about .86 d. The frequency of wrong answers rose as well. The mean rise effect of wrong answers (.30 d) is smaller than the mean rise in right answers, but it is also evident in 7 of the 9 subtests. In the FE framework it is important to note that the diminishing number of missing answers is offset by, not only right answers, but wrong answers as well.

Over time the general relationship between right, wrong and missing answers has changed.

One of the clearest findings in both cohorts is that instead of right answer there are missing answers. This correlation between the number of correct answers and missing answers was more apparent in 1933/36 (r = -.959, p < .001) than in 2006 (r = -.872, p < .001). In 1933/36 the number of wrong answers did not correlate with the number of right answers (r = -.005), but in 2006 the frequency of wrong answers moderately indicates a low number of right answers (r = -.367, p < .001). In both cohorts the number of missing answers is negatively correlated with wrong answers, but the relationship is stronger in the 2006 cohort (r = -.277, p < .001; in 1933/36 r = -.086, p = .01). The cohort differences between the above presented correlations across cohorts are statistically significant.

Besides, Must (2013, Figure 1) also shows that after adjustment for wrong answers, the effect size is reduced among subtests, although at different degrees. His Table 4 displays the changes of odds to give a right, wrong or missing answer at the item level. The odds of both right and wrong answers were rising. The changes in response structure is further evidenced (Table 5) by the correlation between wrong answers and order of items (i.e., odds of giving a wrong answer at the end of a subtest). This relationship displays no clear pattern for the 1933/36 cohort (mean rho = 0.086) while it was positive for the 2006 cohort (mean rho = 0.426). As Must mentioned, “The 2006 cohort tried to solve more items, but in a more haphazard way than did the cohort of 1933/36. The main difference between cohorts is the test-taking speed. But speed has its price – the more items that students tried to solve, the higher the probability of answering incorrectly as well (Table 5)”. The subtests are organized according to an increasing scale of difficulty, and so, the attempt to answer more items results in more errors “especially so if the items required attention and thought or the test-takers are hurrying towards the end of test”. But because the hardest test items are likely to be the most complex, this suggests a possibility that a substantial portion of the IQ gains due to guessing must be exceedingly g-loaded. Woodley et al. (2014) answered the question. Using Must (2013) Estonian data, they found a correlation between g-loadings and gains of -0.180 and -0.471 for the vector gains uncorrected and corrected for guessing. On the other hand, the vector gain owing to guessing correlates at 0.945 with IQ gains. The correlation between difficulty and complexity, according to one study they cite, was 0.52, but since measurement error (especially at the item level) reduces the correlation, they corrected it for this artifact and estimated a corrected r=0.93.

Neisser (1997) hypothesized that the IQ gain was due to increased exposure to complex visual and technical environments. Those two variables have moved over time in the same direction but this does not imply that individuals most exposed to this environment have higher fluid IQs. Sigal & McKelvie (2012, Tables 3 & 4) attempt to test that hypothesis, by correlating the amount of time spent playing video games (3-D and 2-D) and/or puzzles, watching TV/movies, and test scores in visual skills. In multiple regression, these variables have collectively a good relationship with mental rotation skills (r=0.554 for accuracy and r=0.514 for weighted accuracy). They then correlate these same variables with Cattell Culture Fair Test (CCFT or CFIT) and the Wide Range Vocabulary Test (WRVT). Sample size was 154. The model R² was 0.038 for CCFT, which gives an effect size of SQRT(0.038)=0.195. The R² was 0.139 for WRVT, or r=0.373. Note that the R² does not necessarily produce positive r. The correlations of 2-D and 3-D video games, TV/movie, and puzzle, with CFIT are 0.032, 0.010, -0.114, 0.082. There is no good evidence for the hypothesis.

Flynn (1999, p. 9) is also skeptical about Neisser’s hypothesis. The Similarities subtest from the Wechsler’s scale shows by far the greatest gain. It is a test of fluid g, but it has a purely verbal format. The Raven and the performance subtests of the Wechsler, by contrast, have a visuospatial format. Even though it is true that performance IQ increased more than verbal IQ.

In aging IQ studies, it is important to adjust for cultural change in order to separate artifact gains and real gains. This is what Kaufman (2010a, pp. 390-392, 2010b, p. 498) explained in a discussion with Flynn (2010b) regarding the secular gains on fluid and crystallized abilities.

The item type used in Similarities resembles the age-old questions that teachers have asked children in schools for generations. In contrast, matrices-type items were totally unknown to children or adults of yesteryear and remained pretty atypical for years. Over time, however, this item type has become more familiar to people around the world, especially as tests of this sort have been increasingly used for nonbiased assessment, including for the identification of gifted individuals from ethnic minorities. And, because Raven’s tests can be administered by nonpsychologists, these items tend to be more accessible to the public than are items on Wechsler’s scales, which are closely guarded because of the clinical training that is a requisite for qualified examiners. But go to any major bookstore chain, or visit popular websites, and you can easily find entire puzzle books or pages of abstract matrix analogies.

It is, therefore, difficult to evaluate gains on matrices tasks without correcting these gains for time-of-measurement effects. The power of this “time lag” variable was demonstrated by Owens in his groundbreaking longitudinal study of aging and intelligence. Owens (1953) administered the Army Alpha test in 1950 to 127 men, age 50, who had been administered the same test in 1919 at age 19, when they were freshmen at Iowa State University (initial N = 363). The study continued in 1961 when 96 of these men were tested again, at age 61 (Owens, 1966).

The 96 men tested three times improved in verbal ability between ages 19 and 50 followed by a slight decline from age 50 to 61. On nonverbal reasoning ability, they displayed small increments from one test to the next. However, Owens had the insight to also test a random sample of 19-year-old Iowa State freshmen on the Army Alpha in 1961 to 1962 to permit a time-lag comparison. He was able to use the data from the 19-year-olds to estimate the impact of cultural change on the obtained test scores. When Owens corrected the data for cultural change, the Verbal scores continued to show gains between ages 19 and 61; but what had appeared to be small increments in Reasoning were actually steady decreases in performance.

The time-lag correction may reflect real differences in mental ability (i.e., FE) as well as changes in test-taking ability and familiarity with a particular kind of task. The mere fact of large gains on a test such as Raven’s matrices over several generations, in and of itself, cannot be interpreted unequivocally as an increase in abstract reasoning ability without proper experimental controls. When Flynn has interpreted gain scores for groups of individuals tested generations apart on the identical Raven’s matrices items (e.g., Flynn, 1999, 2009a), he has not controlled for time-of-measurement effects.

So, after controlling for cultural change (scores of 19-years-olds in 1961 minus scores of 19-years-olds in 1919), the small fluid IQ gain with age becomes negative while verbal IQ gain with age is robust to cultural change. There were only two tests of fluid IQ, however.

Another account of lack of measurement equivalence is from Kanaya & Ceci (2011). When children were tested on an old version (norm) of the Wechsler (WISC-R) and retested on a newer version (WISC-III) supposed to be more difficult, significant IQ decline had been observed as compared to the group being tested and retested on WISC-R. The group tested and retested on the new norm WISC-III was not so different from the group tested and retested on the old norm WISC-R (Table 3) after controlling for age, initial IQ and practice effect (i.e., with time between tests).

On the condition we can disregard Flynn gains among infants, measurement bias (through test familiarity) effectively decreases test g-loadedness, and there is convincing proof that test g-loadedness has declined, thus accounting for the hollow IQ gains. But if cultural bias cannot account for the Flynn effect, then cultural bias is not the leading cause behind the decline in the strength of g. As we will see, the life history model proposes a better alternative.

9 ) Life history model.

Woodley (2011a, 2012) is a proponent of the idea. The model is based on the fact that, over time, people tend to opt for a K-oriented strategy, i.e., less offspring, more investment, slow life history, as opposed to r-oriented strategy, i.e., more offspring, less investment, rapid life history. One consequence of the theory is that the strength of the g factor diminishes over time, as people rely less on g, but more on specialized abilities.

To illustrate, the model can predict why education is not g-loaded, since education is a source of slowing life history. More educated people can invest more in specialized abilities. This would be predicted as a result of the division of labour, a feature of economies associated with complexity. In light of this, we must understand that the role of g has declined because g becomes less beneficial whereas specialization is more needed than before.

Some researchers investigated the issue of Spearman’s law of diminishing returns. It has been reported that the Flynn Effect originated from an increase in specific, not general abilities. For instance, using the WAIS, WAIS-R, WAIS-III, Kane (2000, p. 565; & Oakland, 2000, p. 343) found that the subtest intercorrelations (or positive manifold) had decreased over time, which induces him to conclude that “lower test intercorrelations may not reflect a diminishment in the importance of g per se, but rather the improvement of specific primary cognitive abilities”, as one plausible explanation. Juan-Espinosa (2006), on its part, says the following :

The indifferentiation hypothesis has relevant practical implications. First of all, it can be assumed that Wechsler batteries are measuring the same g factor across all age groups. This being true, social correlates of the Wechsler’s scales as the prediction of the educational achievement or the likelihood of being out from the school (e.g., Neisser, Boodoo, Bouchard, Boykin, Brody, Ceci, Halpern, Loehlin, Perloff, Sternberg and Urbina, 1996) would be mostly due to the g factor (Jensen, 1998). However, the same cannot be said of the comparison across cohorts. The youngest cohorts depend more on non-g factors to achieve a higher performance level.

Similar findings were previously reported by Lynn & Cooper (1993, 1994). This outcome of course was inescapable insofar as Flynn Effect results in increases in specific abilities rather than general abilities. By the same token, the specialization and differentiation of abilities appear wholly consistent with Woodley’s cognitive differentiation-integration effort (CD-IE) hypothesis (2012, 2011a). Low-IQ people are more dependent on g than those with higher IQ, who can rely on a wider array of abilities. Here is, in short, how Woodley describes his model :

The tradeoff concerns two hypothetical types of effort – cognitive integration effort (CIE), associated with a strengthening of the manifold via the equal investment of bioenergetic resources (such as time, calories and cognitive real estate) into diverse abilities, and cognitive differentiation effort (CDE), associated with a weakening of the manifold via the unequal investment of resources into individual abilities.

For instance, while many researchers believe that nutrition and/or education, among other things, are behind the Flynn Effect, Woodley (2012) tells us that any factor reducing diseases, mortality, or improving health, adequate nourishment, education, environment as a whole, would permit the development of differentiated abilities and consequently the hollow gains in the Flynn Effect. Four successful tests of the CD-IE effect (Woodley et al., 2013) show that it shares with the Flynn Effect the same psychometric properties, namely the absence of Jensen Effect, making it once again a candidate for the explanation of the secular gains.

Apparently, the theory does not predict that IQ gains are the mere product of artifacts, but only reflect a diminishing return of g, which may imply that IQ gains must have some real-world consequences, as Woodley even recognizes that non-g abilities have predictive validity. The absence of real-world effects is not reconcilable with the model.

Although there seems to be ample evidence in support of the theory, there is still another problem. How can the model explain the declining g-loadedness in the test scores given to infants, assuming it has even occurred ? The inability to answer this question must lead to a rejection of the model.

10 ) Rule-dependence model.

Armstrong & Woodley (2014) argue that the huge gains in fluid IQ, especially seen in the Raven, is the result of the so-called rule-dependence on what the Raven relies on. It was stated that earlier cohorts are more sensitive to tests that rely on “rule” inferences such as the kind elicited by Raven-like tests. It is predicted that IQ tests that don’t rely on rule inferences and/or tests that elicit more complex and less predictable rule-sets (e.g., Cattell Culture Fair tests) will show smaller IQ gains.

In essence, the more reliant a particular test is on the identification and repeated use of specific rule-sets, the bigger the Flynn and retesting effects. ... Our theory thus provides a potential solution to the “Raven’s paradox”, as it is proposed that tests like the RPM are only highly g loaded when encountered initially.

The simple fact that FE gains occur among infants is sufficient to reject their model, which is based on knowledge exposure and test familiarity. Flynn (1987) in his review had already expected that knowledge was not a meaningful factor even though he has changed his views.

If we remember that Fox & Mitchum (2012) found that the newer cohorts exhibit less capability to infer the so-called rules in the Raven, when total raw score is equated, we must understand that such result shows the opposite pattern of what the rule-dependence model predicts. The members of earlier (newer) cohorts are simply more able to map dissimilar objects.

Besides, Armstrong & Woodley (2014) have committed a mistake when they relate the common claim that because the Raven, one of the most highly g-loaded test, and a highly culture-reduced test above all, shows larger gains than culture-loaded tests, then this simple fact sheds some doubt that Flynn gains would be uncorrelated with g. That argument was not valid to begin with. The between-test comparison is not always appropriate as it can be confounded by test properties. Jensen (1998, p. 369) made it clear that a test of Spearman hypothesis should not only be studied across subtests having each different properties but also within (sub)tests. With respect to race differences, Jensen argues :

IQ tests are seldom composed of homogeneous items. (The Raven matrices is the best-known example of one that is.) For most IQ tests the total score is typically based on an amalgam of heterogeneous item types or of subtests that differ in the particular types of knowledge or skill they demand and in their factor composition. Unfortunately, the almost exclusive emphasis on the black-white IQ difference in discussions of population differences has eclipsed the telling fact that the size of the group difference varies greatly across different (homogeneous) cognitive tests. This is especially regrettable from a research standpoint, because the great variability of the W-B difference across various tests can help us discover the psychometric basis of that difference.

Another problem with the rule-dependence theory is the absence of evidence that measurement bias accounts for the majority or totality of the Flynn gains, thus nullifying their model.

3. What to conclude.

None of the proposed hypotheses, either taken individually or combined, is satisfying. But if we were to weigh the hypotheses against each other, hypothesis n°1 has some relevance. If true, the modest evidence of an absence of any trend in RT and IT scores would prove once again that psychologists for more than 100 years by now went all the wrong way.

The reason why the “g” argument is actually irrelevant is not due to the fact that the g model is irrelevant but because the current tests of Spearman’s effect are sub-optimal. Jensen (1998, pp. 332-333) probably understood this problem, as he has suggested this line of research :

Therefore, if the subject is to be researched in the future, it will call for an innovative methodology and an additional kind of data. As I have suggested elsewhere, [42] conventional psychometric raw scores will need to be anchored to measures that presumably are not influenced by the environmental variables that raise test scores without increasing g. The anchor variables would consist of measures of reaction time to various elementary cognitive tasks, evoked brain potentials, nerve conduction velocity, and the like, that are demonstrably g-loaded. (A composite measure based on the anchor variables should have a reasonably high correlation [say, r > .50] with the psychometric test scores.) Mental test raw scores would be regressed on these anchor variables in a representative sample of some population. A later comparable sample would be matched to the earlier sample on the anchor variables. This later sample’s raw scores (on the very same psychometric test) then would be regressed on the anchor variables. [43] A significant difference between the regression lines of the earlier and the later tested groups would indicate that the psychometric scores were not measuring the same thing in each group. Thus the secular increment in mean score wouldn’t mean simply “more of the same.” If the regression lines remained the same, however, it would indicate that any significant observed mean raw-score difference between the groups was a real difference in whatever the test measured at both points in time. That is, the mean gain would be reflected in the anchor variables as well as in the test scores.

It seems Jensen did not understand that means (intercepts) and correlations (slopes) are not necessarily related. The analysis needs only to examine if the gain in IQ scores has been accompanied by an improvement in the anchor variables. This is how the Spearman hypothesis should be really tested. MCV, PCA or MGCFA, none of these techniques is relevant.

References :

1. Ang SiewChing, Rodgers Joseph Lee, & Wänström Linda (2010). The Flynn Effect within subgroups in the U.S.: Gender, race, income, education, and urbanization differences in the NLSY-Children data.

2. Armstrong Elijah L., & Woodley Michael A. (2014). The rule-dependence model explains the commonalities between the Flynn effect and IQ gains via retesting.

3. Ashton Michael C., & Lee Kibeom (2005). Problems with the method of correlated vectors.

4. Bakhiet Salah eldin Farah Attallah, Barakat Serry Mohammed Roshdy, Lynn Richard (2014). A Flynn effect among deaf boys in Saudi Arabia.

5. Bandeira Denise R., Costa Angelo, & Arteche Adriane (2012). The Flynn effect in Brazil: Examining generational changes in the Draw-a-Person and in the Raven’s Coloured Progressive Matrices.

6. Batterjee Adel A., Khaleefa Omar, Ali Khalil, Lynn Richard (2013). An increase of intelligence in Saudi Arabia, 1977-2010.

7. Beaujean A. Alexander, & Osterlind Steven J. (2008). Using Item Response Theory to assess the Flynn Effect in the National Longitudinal Study of Youth 79 Children and Young Adults data.

8. Beaujean A. Alexander, & Sheng Yanyan (2010). Examining the Flynn Effect in the General Social Survey Vocabulary test using item response theory.

9. Carpenter Patricia A., Just Marcel Adam, and Shell Peter (1990). What One Intelligence Test Measures: A Theoretical Account of the Processing in the Raven Progressive Matrices Test.

10. Chuck, Race, genes, and disparity (February 17, 2011). Spearman’s hypothesis and the Jensen Effect.

11. Cotton, S. M., Kiely, P. M., Crewther, D. P., Thomson, B., Laycock, R., & Crewther, S. G. (2005). A normative and reliability study for the Raven’s Colored Progressive Matrices for primary school aged children in Australia.

12. Dickens William T. (2005). Genetic Differences and School Readiness.

13. Dickens William T. (2009). A Response to Recent Critics of Dickens and Flynn (2001).

14. Dickens William T., and Flynn James R. (2001). Heritability estimates versus large environmental effects: The IQ paradox resolved.

15. Dickens William T., and Flynn James R. (2002). The IQ Paradox: Still Resolved.

16. Dodonova Yulia A., & Dodonov Yury S. (2013). Is there any evidence of historical slowing of reaction time? No, unless we compare apples and oranges.

17. Dolan Conor. V. (2000). Investigating Spearman’s hypothesis by means of multi-group confirmatory factor analysis.

18. Dolan Conor V., and Hamaker Ellen L. (2001). Investigating black–white differences in psychometric IQ: Multi-group confirmatory factor analysis of the WISC-R and K-ABC and a critique of the method of correlated vectors.

19. Flynn James R. (1987). Massive IQ Gains in 14 Nations: What IQ Tests Really Measure.

20. Flynn, J. R. (1999). Searching for justice: the discovery of IQ gains over time. American Psychologist, 54(1), 5.

21. Flynn, James R. (2000). IQ gains, WISC subtests, and fluid g: g-theory and the relevance of Spearman’s hypothesis to race. In G. R. Bock, J. A. Goode, and K. Webb (Eds.), The Nature of Intelligence (pp. 202-227). New York: Wiley.

22. Flynn James R. (2009). Requiem for nutrition as the cause of IQ gains: Raven’s gains in Britain 1938–2008.

23. Flynn James R. (2010a). The spectacles through which I see the race and IQ debate.

24. Flynn James R. (2010b). Problems With IQ Gains: The Huge Vocabulary Gap.

25. Flynn, J. R., & Rossi-Casé, L. (2012). IQ gains in Argentina between 1964 and 1998. Intelligence, 40, 145–150.

26. Fox, M. C., & Mitchum, A. L. (2013). A Knowledge-Based Theory of Rising Scores on “Culture-Free” Tests. Journal of Experimental Psychology: General, 142(3), 979.

27. Jensen Arthur R. (1973). Educability and Group Differences. London: Methuen.

28. Jensen Arthur R. (1980). Bias in Mental Testing. New York: Free Press.

29. Jensen Arthur R. (1998). The g Factor: The Science of Mental Ability. Westport CT: Praeger.

30. Jensen, A. R. (2006). Clocking The Mind: Mental Chronometry and Individual Differences. Elsevier.

31. Juan-Espinosa Manuel, Cuevas Lara, Escorial Sergio, & García Luis F. (2006). The differentiation hypothesis and the Flynn effect.

32. Kanaya Tomoe, & Ceci Stephen J. (2011). The Flynn Effect in the WISC Subtests Among School Children Tested for Special Education Services.

33. Kane Harrison D. (2000). A secular decline in Spearman’s g: evidence from the WAIS, WAIS-R and WAIS-III.

34. Kane Harrison D., & Oakland Thomas D. (2000). Secular Declines in Spearman’s g: Some Evidence From the United States.

35. Kaufman Alan S. (2010a). “In What Way Are Apples and Oranges Alike?” A Critique of Flynn’s Interpretation of the Flynn Effect.

36. Kaufman Alan S. (2010b). Looking Through Flynn’s Rose-Colored Scientific Spectacles.

37. Khaleefa Omar, Lynn Richard, Abulgasim Awadala, Dosa Madina, Abdulradi Fadlmula (2010). Norms for the Standard Progressive Matrices for 9-18 year olds for Darfur.

38. Lanfranchi Silvia, & Carretti Barbara (2012). The Increase in Colored Progressive Matrices Test Performance in Individuals With Down Syndrome: A Qualitative and Quantitative Review.

39. Loehlin John C. (2002). The IQ Paradox: Resolved? Still an Open Question.

40. Lubke Gitta H., Dolan Conor V., Kelderman Henk, and Mellenbergh Gideon J. (2003). On the relationship between sources of within- and between-group differences and measurement invariance in the common factor model.

41. Lynn Richard (2009a). What has caused the Flynn effect? Secular increases in the Development Quotients of infants.

42. Lynn Richard (2009b). Fluid intelligence but not vocabulary has increased in Britain, 1979-2008.

43. Lynn Richard (2013). Who discovered the Flynn effect? A review of early studies of the secular increase of intelligence.

44. Lynn Richard, & Cooper Colin (1993). A secular decline in Spearman’s g in France.

45. Lynn Richard, & Cooper Colin (1994). A Secular Decline in the Strength of Spearman’s g in Japan.

46. Metzen Daniel (2012). The Causes of Group Differences in Intelligence Studied Using the Method of Correlated Vectors and Psychometric Meta-Analysis.

47. Mingroni Michael A. (2004). The secular rise in IQ: Giving heterosis a closer look.

48. Mingroni Michael A. (2007). Resolving the IQ Paradox: Heterosis as a Cause of the Flynn Effect and Other Trends.

49. Murray Charles (2005). The Inequality Taboo.

50. Must Olev, Must Aasa, & Raudik Vilve (2003). The secular rise in IQs: In Estonia, the Flynn effect is not a Jensen effect.

51. Must Olev, & Must Aasa (2013). Changes in test-taking patterns over time.

52. Must Olev, te Nijenhuis Jan, Must Aasa, and van Vianen Annelies E.M., 2009, Comparability of IQ scores over time.

53. Nedelec Joseph L., Schwartz Joseph A., Connolly Eric J., Beaver Kevin M. (2012). Exploring the association between IQ and differential life outcomes: results from a longitudinal sample of monozygotic twins.

54. Nettelbeck Ted, & Wilson Carlene (2004). The Flynn effect: Smarter not faster.

55. Pietschnig Jakob, Tran Ulrich S., Voracek Martin (2013). Item-response theory modeling of IQ gains (the Flynn effect) on crystallized intelligence: Rodgers’ hypothesis yes, Brand’s hypothesis perhaps.

56. Rodgers Joseph L. (1999). A Critique of the Flynn Effect: Massive IQ Gains, Methodological Artifacts, or Both?.

57. Rönnlund Michael, Carlstedt Berit, Blomstedt Yulia, Nilsson Lars-Göran, and Weinehall Lars (2013). Secular trends in cognitive test performance: Swedish conscript data 1970–1993.

58. Rowe David C., & Rodgers Joseph L. (2002). Expanding Variance and the Case of Historical Changes in IQ Means: A Critique of Dickens and Flynn (2001).

59. Rushton J. Philippe (1999). Secular gains in IQ not related to the g factor and inbreeding depression – unlike Black-White differences: A reply to Flynn.

60. Rushton J. Philippe, and Jensen Arthur R. (2010). The rise and fall of the Flynn Effect as a reason to expect a narrowing of the Black–White IQ gap.

61. Shayer Michael, Ginsburg Denise, & Coe Robert (2007). Thirty years on – a large anti-Flynn effect? The Piagetian test Volume & Heaviness norms 1975-2003.

62. Shayer Michael, Ginsburg Denise (2009). Thirty years on - a large anti-Flynn effect (II): 13- and 14-year-olds. Piagetian tests of formal operations norms 1976-2006/7.

63. Shiu William, Beaujean A. Alexander, Must Olev, te Nijenhuis Jan, Must Aasa, 2013, An item-level examination of the Flynn effect on the National Intelligence Test in Estonia.

64. Sigal, M. J., & McKelvie, S. J. (2012). Is Exposure to Visual Media Related to Cognitive Ability? Testing Neisser’s Hypothesis for the Flynn Effect. Journal of Articles in Support of the Null Hypothesis, 9(1), 24.

65. Sundet Jon Martin, Barlaug Dag G., Torjussen Tore M. (2004). The end of the Flynn effect? A study of secular trends in mean intelligence test scores of Norwegian conscripts during half a century.

66. Sundet Jon Martin, Eriksen Willy, Borren Ingrid, Tambs Kristian (2010). The Flynn effect in sibships: Investigating the role of age differences between siblings.

67. te Nijenhuis Jan (2012). The Flynn effect, group differences, and g loadings.

68. te Nijenhuis Jan, van Vianen Annelies E.M., van der Flier Henk (2007). Score gains on g-loaded tests : No g.

69. te Nijenhuis Jan, & van der Flier Henk (2013). Is the Flynn effect on g?: A meta-analysis.

70. te Nijenhuis Jan, Murphy Reagan, van Eeden Rene (2011). The Flynn effect in South Africa.

71. Wai Jonathan, & Putallaz Martha (2011). The Flynn effect puzzle: A 30-year examination from the right tail of the ability distribution provides some missing pieces.

72. Wicherts Jelte M., & Dolan Conor V. (2010). Measurement Invariance in Confirmatory Factor Analysis: An Illustration Using IQ Test Performance of Minorities.

73. Wicherts Jelte M., Dolan Conor V., Hessen David J., Oosterveld Paul, van Baal G. Caroline M., Boomsma Dorret I., Span Mark M. (2004). Are intelligence tests measurement invariant over time? Investigating the nature of the Flynn effect.

74. Williams L. Robert (2013). Overview of the Flynn effect.

75. Woodley Michael A. (2012). A life history model of the Lynn–Flynn effect.

76. Woodley Michael A. (2011a). The Cognitive Differentiation-Integration Effort Hypothesis: A Synthesis Between the Fitness Indicator and Life History Models of Human Intelligence.

77. Woodley Michael A. (2011b). Heterosis Doesn’t Cause the Flynn Effect: A Critical Examination of Mingroni (2007).

78. Woodley Michael A., & Figueredo Aurelio José, Brown Sacha D., Ross Kari C. (2013). Four successful tests of the Cognitive Differentiation-Integration Effort hypothesis.

79. Woodley Michael A., & Madison Guy (2013). Establishing an association between the Flynn effect and ability differentiation.

80. Woodley Michael A., & Meisenberg Gerhard (2013). In the Netherlands the anti-Flynn effect is a Jensen effect.

81. Woodley Michael A., te Nijenhuis Jan, Must Olev, Must Aasa (2014). Controlling for increased guessing enhances the independence of the Flynn effect from g: The return of the Brand effect.