Hollow Flynn Effect in Two Developing Countries and A Further Test of the Debatable Black-White Genetic Differences
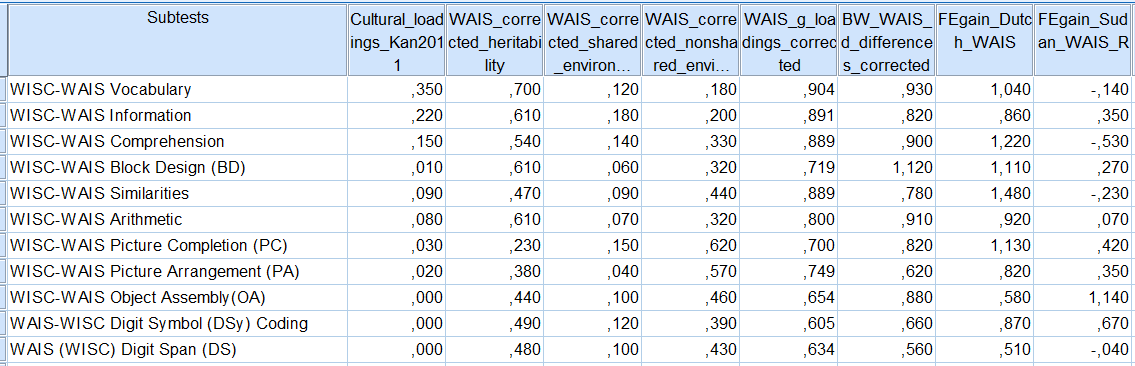
Studies of the nature of the Flynn Effect are usually done in developed countries (e.g., Rushton, 1999; Wicherts, 2004; Nijenhuis, 2007; for an ‘Overview of the Flynn Effect’, see Williams, 2013). There are two recent data on two developing countries (Khaleefa, 2009; Liu, 2012). The reported numbers on subtests gains can be studied using either MCV or PC analysis. Next, we will see that shared (c²) and non-shared (e²) environments, as measured by Falconer’s formula, are unrelated to heritability (h²) of the WAIS and WISC subtests. Culture load, heritability, g-loadings, and black-white differences tend to form a common cluster (on PC1) that is different from the pattern of loadings shown by shared and non-shared environment. The data I am using here is summarized in this XLS. It contains the references of the relevant data and calculations. Below is the SPSS table showing the column vectors of the variables.
Using these numbers, a correlation matrix and a component matrix are produced. For the latter, I use the correlation matrix from Spearman correlation because it is known to be more robust to outliers than Pearson. But, in fact, PC analysis produce more or less the same pattern of loadings if I use Pearson.
While the vector of shared environment is correlated with the vector of culture load and somewhat with g-loadings, it has its highest loadings on a different component, meaning that they behave in different ways. As can be seen, culture load, heritability, g-loadings and BW differences tend to form a cluster on PC1 with significant loadings. Shared, non-shared environment and Sudan gain (from Khaleefa 2009) are loaded positively on a different component. Dutch gain (from Wicherts 2004) is loaded almost equally on PC1 and PC2. With regard to the measurement bias question, Wicherts (2004) said about the WAIS Dutch gains :
The model with identical configuration of factor loadings in both cohorts (Model 1: configural invariance) fits poorly in terms of χ². However, the large χ² is due to the large standardization sample (χ² is highly sensitive to sample size; Bollen & Long, 1993), and the RSMEA and CFI indicate that this baseline model fits sufficiently. In the second model (Model 2: metric invariance), we restrict factor loadings to be equal across both cohorts (i.e., Λ1=Λ2). All fit indices indicate that this does not result in an appreciable deterioration in model fit, and therefore, this constraint seems tenable. However, the restriction imposed on the residual variances (Model 3: Θ1=Θ2) is not completely tenable because AIC and Δχ² indicate a clear deterioration in fit as compared with the metric invariance model. However, RMSEA, CFI, and CAIC indicate that this restriction is tenable. In a formal sense, residual variances are unequal across groups, although the misfit due to this restriction is not large. More importantly, both models (4a and 4b) with equality constraints on the measurement intercepts (ν1=ν2) show insufficient fit. The RMSEA values are larger than the rule-of-thumb value of 0.05, and (C)AICs show larger values in comparison with the values of the third model. Although the CAIC values of Models 4a and 4b are somewhat lower than the CAIC of the unrestricted model (reflecting CAIC’s strong preference for parsimonious models), the difference in χ² comparing Models 4a and 4b to less restricted models is very large. [3] Both strong and strict factorial invariances therefore appear to be untenable.
Next is the data from Liu (2012) for WPPSI subtest gains. I used the g-loadings reported by Roid & Gyurke (1991) and Liu (2011). The latter reports the rotated factor loadings, not the unrotated loadings. As Jensen (1980, p. 209) noted, a first factor after rotation is no longer a general factor. The numbers are shown below :
Once again, from the above correlation matrix, the negative correlation between g-loadings and secular gains appears to be crystal clear, in line with the other studies.
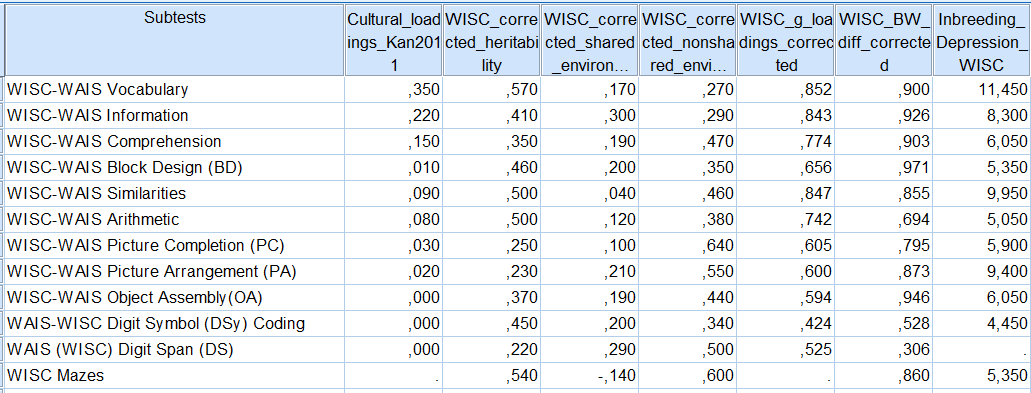
For the last analysis, now, I will replicate the previous PC analysis using this time the data from WISC subtests. Below is the SPSS table showing the column vectors of the variables.
With these numbers, I produced the following correlation matrix and component matrix again using Spearman rho.
The pattern of correlations and components appear similar to what is shown using WAIS data (with the exception of BW differences, loaded equally well on PC1 and PC2), namely, the total absence of relationship between c² and e² with h² and g. At the same time, the cuture-loadedness of the tests is related to their heritabilities and g-loadedness. This however looks surprising.
Now, given all these numbers, what need to be said ? At first glance, the positive correlation between culture load and g and heritability is difficult to explain from the hereditarian viewpoint, if Kees-Jan Kan words were to be believed. This result, among other things, lead him to conclude in his PhD thesis (2011, ch. 3 & 4) that the genetic origin of the black-white differences, as posited (e.g.) by Rushton and Jensen, could be nothing more than “Weak inferences based on ambiguous results”. But at the same time, the above PC analyses showed that c² and e² are loaded significantly on a different component than PC1, which comprises the highest loadings for h² and cultural load. This pattern, of course, cannot be explained by the cultural hypothesis.
And because we haven’t discussed it yet. What are the characteristics of a culture-loaded test ? Kan (2011, Table 3.1, Figure 3.3) considers the culture-loaded tests as the crystallized ones, and the culture-reduced tests as the fluid ones. The reason is that, as Kan said, “Fluid tests minimize the role of individual differences in prior knowledge, whereas crystallized tests maximize it”, thus meaning that fluid tests are more reflective of cognitive processes while crystallized tests are more reflective of acquired skills and knowledge. Kan cites Jensen’s own definition of a culture-biased test :
“Tests and test items can be ordered along a continuum of culture loading, which is the specificity or generality of the informational content of the test items. The narrower or less general the culture in which the test’s information could be acquired, the more cultural loaded it is. A test may contain information that could only be acquired within a particular culture. This can actually be determined simply by examination of the test items. The specificity or generality of the content corresponds to its cultural loading.” (Jensen, 1976, p.340)
More on this can be read in Jensen (1980, pp. 133, 234-235, 374, 538-539, 635-637; 1998, pp. 123-126). Also important to keep in mind is that a culture-reduced test should maintain the same psychometric properties, or parameters, meaning that the tests behave the same way across groups (e.g., race, gender, cohort). As Jensen says, in Bias in Mental Testing :
Culture-reduced items are nonverbal and performance items that do not involve content that is peculiar to a particular period, locality, or culture, or skills that are specifically taught in school. Items involving pictures of cultural artifacts such as vehicles, furniture, musical instruments, or household appliances, for example, are culture loaded as compared with culture-reduced items involving lines, circles, triangles, and rectangles.
Operationally, we can think of the degree of “culture reducedness” of a test in terms of the “cultural distance” over which a test maintains substantially the same psychometric properties of reliability, validity, item-total score correlation, and rank order of item difficulties. Some tests maintain their essential psychometric properties over a much wider cultural distance than others, and to the extent that they do so they are referred to as “culture reduced.” Certain culture-reduced tests, such as Raven’s Progressive Matrices and Cattell’s Culture Fair Test of g, have at least shown equal average scores for groups of people of remotely different cultures and unequal scores of people of the same culture and high loadings on a “fluid” g factor within two or more different cultures. Such tests apparently span greater cultural distances than do tests that involve language and specific informational content and scholastic skills.
If we accept this premise, then I would not reach the same conclusion as Kan (2011, p. 56) did, when he affirms that the black-white differences are larger on the more cultural-influenced tests. It remains to be seen that crystallized tests, as compared with fluid tests, really behave differently across groups. While Jensen argued (1980, p. 133) that culture-loaded tests are not necessarily culture-biased, he has made it clear that a culture-influenced test should be manifested through between-group differences in the meanings of the tests/items. Given some tests of measurement equivalence done using the WISC tests (Dolan, 2000; Lubke, 2003), there is no clear evidence of psychometric bias across racial groups. Furthermore, a positive BW difference correlation with culture load is not always found, far from it. Using a different procedure for classifying culture loaded tests, Jensen and McGurk (1987, p. 298) showed that the BW difference is larger on culture-reduced tests while holding constant item difficulty (see also, Jensen, 1977, pp. 56-62; Reynolds & Gutkin, 1981, pp. 178-179; Jensen & Reynolds, 1982, pp. 426-427; Reynolds & Jensen, 1983, pp. 210-213). Given the extensive literature on this subject reviewed by Jensen (1973, ch. 4, 12, & 17; 1980, ch. 10, 11 & 12; 1998, ch. 11), I must maintain that the BW differences are larger on culture-reduced tests.
References :
Dolan (2000). Investigating Spearman’s hypothesis by means of multi-group confirmatory factor analysis.
Lubke (2003). On the relationship between sources of within- and between-group differences and measurement invariance in the common factor model.
Jensen (1973). Educability and Group Differences.
Jensen (1977). An Examination of Culture Bias in the Wonderlic Personnel Test.
Jensen (1980). Bias in Mental Testing.
Jensen (1998). The g Factor.
Jensen & McGurk (1987). Black-white bias in ‘cultural’ and ‘noncultural’ test items.
Jensen & Reynolds (1982). Race, social class and ability patterns on the WISC-R.
Kan (2011). The nature of nurture: the role of gene-environment interplay in the development of intelligence.
Kaufman (1988). Sex, race, residence, region, and education differences on the 11 WAIS-R subtests.
Khaleefa (2009). An increase of intelligence in Sudan, 1987–2007.
Liu (2011). Factor structure and sex differences on the Wechsler Preschool and Primary Scale of Intelligence in China, Japan and United States.
Liu (2012). An increase of intelligence measured by the WPPSI in China, 1984–2006.
Reynolds & Gutkin (1981). A multivariate comparison of the intellectual performance of Black and White children matched on four demographic variables.
Reynolds & Jensen (1983). WISC-R Subscale Patterns of Abilities of Blacks and Whites Matched on Full Scale IQ.
Roid & Gyurke (1991). General-Factor and Specific Variance in the WPPSI-R.
Rushton (1989). Japanese Inbreeding Depression Scores: Predictors of Cognitive Differences Between Blacks and Whites.
Rushton (1999). Secular gains in IQ not related to the g factor and inbreeding depression – unlike Black-White differences: A reply to Flynn.
te Nijenhuis (2007). Score gains on g-loaded tests : No g.
Wicherts (2004). Are intelligence tests measurement invariant over time? Investigating the nature of the Flynn effect.
Williams (2013). Overview of the Flynn effect.
SPSS syntax :
MATRIX DATA VARIABLES=Culture_Load Heritability shared_E nonshared_E g_WAIS BW_diff_WAIS Dutch_gain_WAIS Sudan_gain_WAIS
/contents=corr
/N=5000.
BEGIN DATA.
1
.491 1
.373 .097 1
-.529 -.993 -.174 1
.954 .514 .151 -.547 1
.414 .634 .000 -.589 .428 1
.532 .119 .142 -.091 .445 .433 1
-.575 -.409 .073 .388 -.592 -.203 -.506 1
END DATA.
EXECUTE.FACTOR MATRIX=IN(COR=*)
/MISSING LISTWISE
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO EXTRACTION
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/ROTATION NOROTATE
/METHOD=CORRELATION.MATRIX DATA VARIABLES=Culture_Load Heritability shared_E nonshared_E g_WISC BW_diff_WISC Inbreeding_Depression
/contents=corr
/N=5000.
BEGIN DATA.
1
.455 1
-.281 -.569 1
-.312 -.476 -.333 1
.936 .615 -.393 -.364 1
.257 .133 .161 -.308 .373 1
.613 -.027 .057 -.091 .632 .365 1
END DATA.
EXECUTE.FACTOR MATRIX=IN(COR=*)
/MISSING LISTWISE
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO EXTRACTION
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/ROTATION NOROTATE
/METHOD=CORRELATION.