More children for more happiness ? What is happiness ?

Kanazawa (2004) earlier demonstrated that children would not make the parents happier. Parenthood decreases happiness. Using the GSS data (available here) he was trying to see whether or not an interaction effect (parenthood*married) is substantial with which sign it has but also the impact of parenthood net of the effect of being married. Being married and the interaction term had a positive sign on happiness (dependent variable) while parenthood had a strong negative sign. Here, I will try to replicate that analysis with GSS data using logistic regression. After this, I will comment on Myrskylä and Margolis (2012) study for which my conclusion differs from theirs. Before going any further, one must read my article on multiple regression, and avoid mis-interpreting what a multiple regression really does.

Here are the variables used in the GSS :

Happy_Dichotomy.  0 = Not too happy, 1 = Happy. (Note : Originally, the variable has 1 = Very happy and 2 = pretty happy and 3 = Not too happy. I have just collapsed the first two values into 1. I’m not sure if that was the good way of doing things. On the other hands, I’m not certain about the difference between ‘very happy’ and ‘pretty happy’. Given how the question has been apparently phrased, I found these rather confusing. Whatever the case, I don’t think that question is well-constructed.)

SEX. 1 = MALE, 2 = FEMALE.

WORDSUM. Vocabulary test (a proxy for IQ, correlation = 0.71; 0.83 for g). Should not be taken as a measure of general intelligence however. It is a ten item/question variable, having a rather low reliability, of about 0.73. See “Reliability and Stability Estimates for the GSS Core Items from the Three-wave Panels, 2006–2010” (Michael Hout & Orestes P. Hastings, 2012).

SEI. Respondent socioeconomic index. (range : from ~17 to ~97. It is worth noting that using this variable instead of “realinc” considerably decreases the sample size because there are much less valid cases for this one.)

good_health. 1 = Poor, 2 = Fair, 3 = Good, 4 = Excellent. (Note : Initially, this variable was rather confusing because higher values, that is, response values, were actually indicators of poor health rather than good health. I therefore recoded the variable by inverting all these values.)

MARITAL_STATUS. 1 = Never married, 2 = Married.

POLVIEWS. 1 = Extremely liberal, 4 = Moderate, 7 = Extremely conservative. We hear a lot of talk these days about liberals and conservatives. I’m going to show you a seven-point scale on which the political views that people might hold are arranged from extremely liberal – point 1 – to extremely conservative – point 7. Where would you place yourself on this scale?

ATTEND. 0 = Never, 2 = Once a year, 4 = Once a month, 7 = Every week, 8 = More than once a week. How often do you attend religious services? (Note : Concerning this variable as a proxy for religiousness, I know there are two other variables, GOD and BIBLE, asking some questions about whether we believe in God or whether the Bible is the word of God. But this is misleading. I can easily imagine people saying “I believe in God but I never went to church or even pray”. I don’t think we should call these people religious. Hence, ATTEND must be much more accurate.)

AGE. Respondent’s age.

COHORT. Birth cohort of respondent. (Note : Higher values denoting younger cohorts.)

BW. 1 = White, 2 = Black.

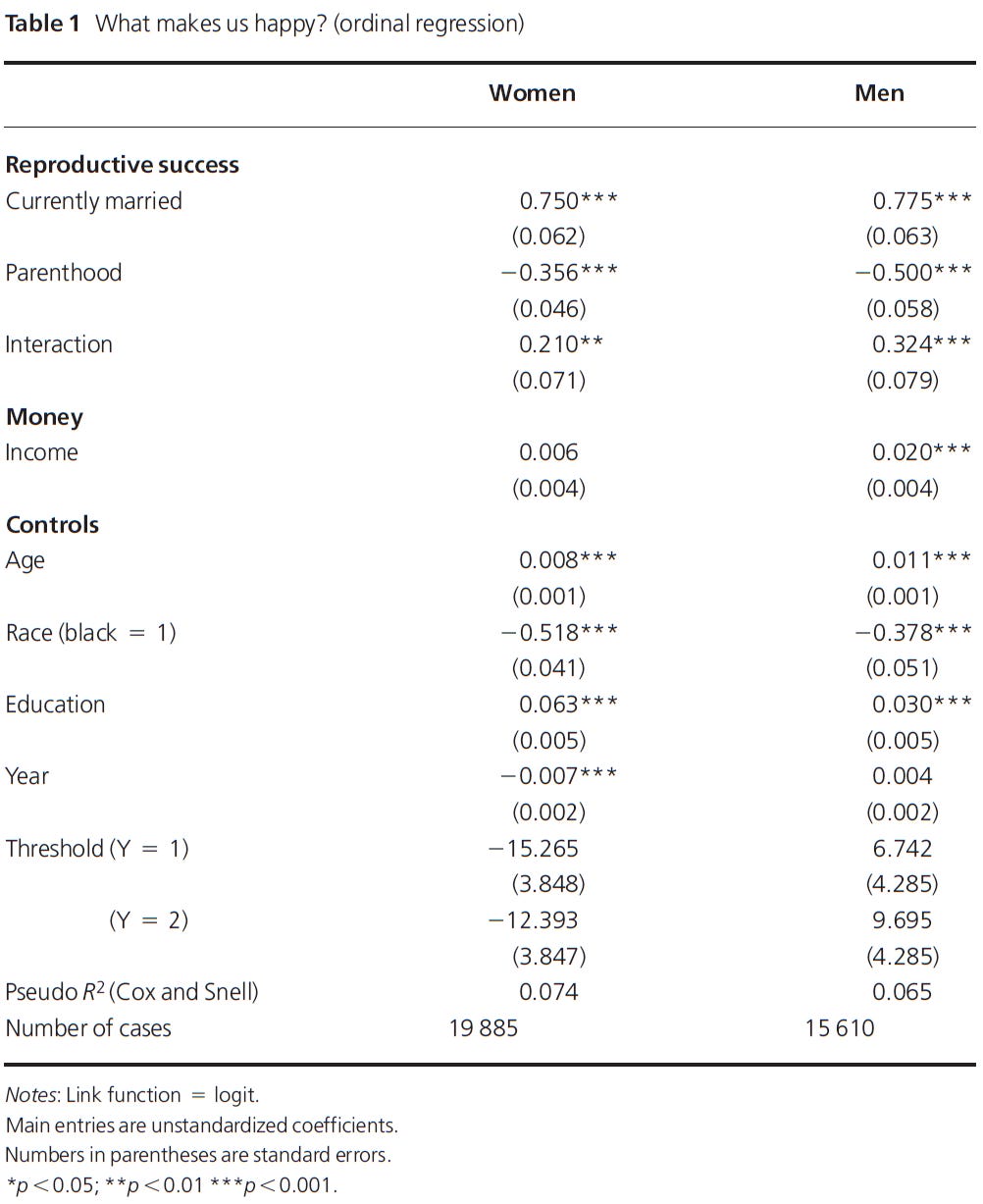
Remember that Kanazawa's table was :

My replication of Kanazawa can be compared :

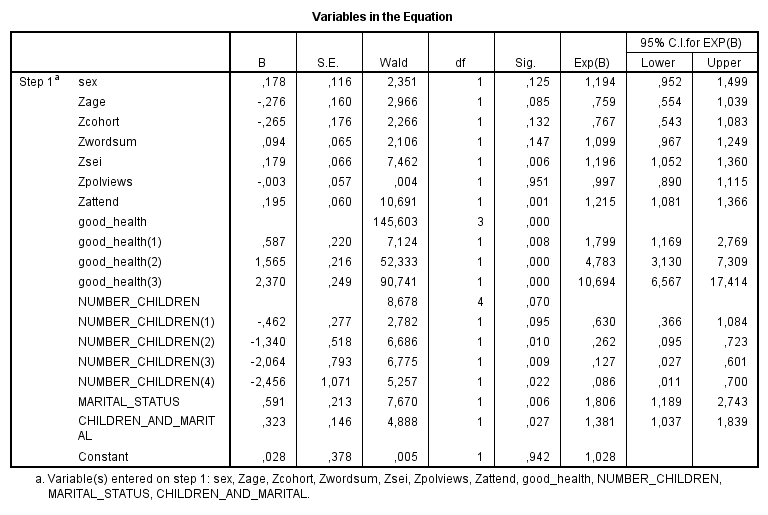
With no doubt I succeeded in replicating Kanazawa (although he uses ordinal regression, and I use logistic regression). I only display the results for the white sample (N=5050). It looks more or less the same when analyzing the black sample (N=719), except that Wordsum had no direct impact whatsoever. The Exp(B) refers to the change in odds ratio attributed to the independent variable. Odds ratio of zero denotes no impact, a value higher than 1 means that the predictor is actually increasing the logit, and a value less than 1 means that it decreases the logit. And Wald is a kind of Chi-square statistics. For a full description of output produced in logistic regression, one might read Field (2009).

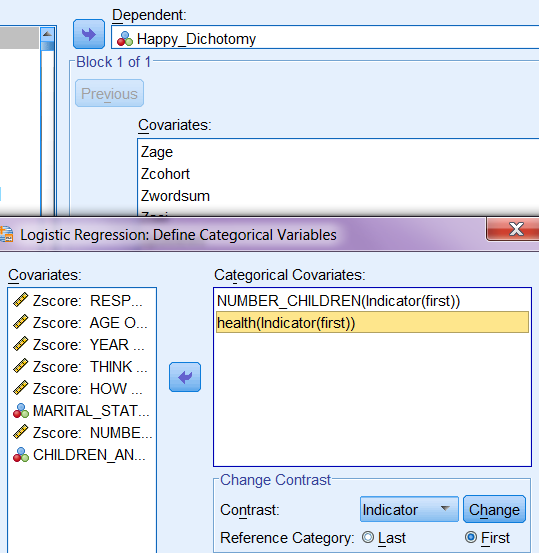
On the question why we see multiple variables for health and children is because I ordered SPSS to define them as categorical variables, as follows :

Because I configured them as “first” indicator, it means that the coefficient for health and children are actually expressed as what happens when health=1 becomes health =2, when health=1 becomes health=3, when health=1 becomes health =4. In other words, the lowest value in health and children variables is defined as the reference category, serving as the point of comparison for the other, higher values. (There is another way to perform this kind of analysis, e.g., by creating dummy variables where the last dummy entered into the regression equation is the variable of reference, as shown below in the syntax.) Good_health (3) has an Exp(B) of 10.694, which is the effect of being classified as being in excellent health (health=4) versus poor health (health=1) on happiness. Good_health (2) has an Exp(B) of 4.783, which is the effect of being classified as being in good health (health=3) versus poor health (health=1) on happiness. And so on.

Now, all of the independent variables, except sex and marital status, have been standardized (z-scores) in order to make comparison easier (see Osborne, 2012). One difference with Kanazawa is that his coefficient for income is near-zero. The likely reason is that he hasn’t standardized his variable, which instead had 12 ordinal categories. In logistic-like regression, the more categories we have, the less is the B coefficient because it expresses the impact of an increase in one value of that variable on the dependent variable. This is why the original income variable should always be zero (if not standardized or categorized) because an increase in one dollar can’t have an impact on whatever dependent variable we may use. Anyway, the positive coefficient for socio-economic status (Zsei) is not surprising, and this was also what I found previously in the NLSY97. Like before, I see that the coefficient for direct effect of health is rather large. In the NLSY97, the best predictor (in terms of direct effect, not total effect) of happiness appeared to be health, not income. And here again, good health appears to be important. No more comments are needed, as we know why. The negative B coefficient for age and cohort suggests that old people and younger cohorts are less happy.

The negative coefficient for cohort is somewhat curious. When I constrain the sample to high- and medium-SES people (N=1978), the coefficient of cohort is positive, that is, younger cohorts seem more happy. On the other hand, constraining the sample to low- and medium-SES people (N=3072) yields a strong negative coefficient for cohort, that is, younger cohorts seem less happy. The first idea that comes to mind is the rise of inequality. I won’t discuss the result for the black sample because it looks too anomalous.

Concerning the impact of SES or income, Kanazawa’s hypothesis was that women should have a less positive coefficient than men, because income is expected to have less positive impact on females’ happiness given this theory. Consistent with that hypothesis, socio-economic status has a more positive effect on white males than on white females. The black sample displays a somewhat different picture, as the effect of SES is large for black males (N=281) but close to zero for black females (N=438).

Now, we see that the more children we have, the less happy we are (when compared to the situation of no children). For Marital Status, because its highest value comprises married people, a positive coefficient indicates more happiness for married people. Now, I also included an interaction term variable, created by just multiplying children*marital. We must be careful about how to interpret such interaction (remembering the last post). It expresses what happens when :

children=0 marital=0

becomes :

children=1 marital=1

In other words, when the values of both children and marital variables increase at the same time. Because the interaction term is positive, that means when the values in children and marital variables both increase, married people with children are more happy than unmarried people with no children. It does not mean that having children per se increases happiness, since children variables have negative signs. It simply means that “married people with children” are more happy than “unmarried people with no children”. For interpreting interaction terms, we must always think that both the variables must move together. One cannot move and the other remains constant. On the other hand, if both of the main effects (children and marital) had positive coefficients, a positive interaction term means that there is some increasing returns. If children and marital add +3 and +6 points of happiness, having both children and being married will not yield +9 points of happiness, but more than this. That is what increasing returns is all about. That’s the interaction effect.

I could have displayed some other statistics as well, such as the Hosmer and Lemeshow goodness of fit. It was 0.907. Because the value is higher than the general cut-off 0.05 (which is purely arbitrary I must add) we may conclude that the model fit is good. However, H&L test is highly sensitive to sample size. The more subjects we have, the more likely we get low H&L value. I do not think we should rely on this. Besides, there is also the Cox & Snell R Square as well as Nagelkerke R Square. The latter is a corrected version of C&S R² because it never attains 1.0, and this is why Nagelkerke is higher than C&S. Anyway, C&S was 0.048 and Nagelkerke was 0.124. What those values denote is not the proportion of variance explained by the set of variables in the actual model, as is the case in multiple regression R². This “pseudo” R-square shows simply the proportion of unexplained variance that is reduced by adding variables in the model. Hence, the larger, the better. Another piece of information about the soundness of the model is the (overall) percentage correct in the classification table. My number was 93.4% meaning that the model actually classifies all the cases with 93.4% of accuracy, which is pretty high. It shows how well the model predicts the data, by comparing observed values against predicted values. The higher the percentage, the better. This classification table translates into this plot :

The 0 and 1 values on the x (i.e. left/horizontal) axis represent the value of the dependent (dichotomized) variable. The cases/subjects who were given a value of 0 should appear on the left hand and those having a value of 1 should appear on the right hand. But when the points are clustered at the center of the graph, this indicates that those cases have about a 50/50 chance that the data are correctly predicted by the model. The more accurate the model is in predicting the actual data, and the further apart the values move away from each other, and the clearer the middle of the (above) graph. When the model is accurate, there will be less misclassification as well. Normally, the 1 values should appear at the right hand or the side having the 1 values, the 0 values at the left hand or the side having the 0 values.

How to interpret this result, now ? Kanazawa speculates the following :

Parents today must raise their children in a radically different environment from the EEA [Environment of Evolutionary Adaptadness]. They must drive them to and from daycare centres and soccer practices, they must put them through compulsory school and pay for their higher education, they must feed, clothe and shelter them in their adolescence and early adulthood (when they would have been economically independent in the EEA soon after puberty), they must purchase computers, cars and other expensive gadgets for them, etc. The list is endless. I suspect that having to raise children in an evolutionarily novel environment might suspend the operation of evolved psychological mechanisms (and the preferences, desires and emotions they engender) and allow other mechanisms to kick in and influence their happiness. Economic and sociological theories are indispensable in explaining these other mechanisms that might overtake and supersede evolved psychological mechanisms in the current environment.

Somehow I agree with the general idea that it must be more difficult to raise children today, thus rendering children less attractive than before (as for myself I can’t speak, I am surely too young for having children right now). One obvious reason is the increasing time allocated for jobs and decreasing time allocated for leisure. But it does not necessarily explain in itself why we become less happy when having children versus none.

When I limit the sample to unmarried people only, I see that having children versus no children decreases happiness and this effect was far much stronger than when I limit the analysis to married people only. Perhaps counter-intuitively, when I constrain the sample to medium and high-SES subjects, the strength of the negative correlation for the children variable seems stronger than the magnitude of this negative correlation when I constrain the sample to medium and low-SES subjects.

This is all I have for within-country analysis. Jayman, in Fertility and Happiness: A Global Perspective, performed some analyses at the between-country level. The best fitted lines shed no doubt on the relationship : countries with higher fertility rates are more happy. Nonetheless, we should be careful about something. To not generalize within-group (or country) to between-group (or country) analyses. Cultural (and even political) differences operating at the between-country level may not operate at the within-country level. The difference in modernization and advancement is probably much wider between countries than within a given country (let alone the fact that any factor which increases one group’s happiness does not necessarily increase the happiness of another group of persons to the same extent, if it does). And these differences can substantially bias the results, rendering generalization a little bit risky, if biases are not statistically (and appropriately) controlled. Hopefully, Jayman constrained the samples (i.e., countries) to high-IQ countries only, which attenuates (but not eliminates) the impact of possible biases.

Cross-sectional analysis is generally not a good tool for analysing causal pathways. And yet the conclusion remains that US people with no children are more happy than US people with children. If we want to know if children are directly related to the lower happiness score of the parents later in life, a longitudinal analysis is the ideal. The only study of this kind I know of is from Myrskylä and Margolis (2012). Apparently, married, older and more educated parents have more positive and lasting happiness. The relevant information has been provided. They separate women and men, high- and low-education people, married and unmarried people. This is a classic but good way for searching influential moderators. An intriguing feature is that self-reported happiness increases before the year of birth for both married and unmarried people. I fully agree with the speculation of the authors; this is most likely due to the expectation of birth and/or new partnership. Also, a finding of interest is that having a second child does not really add to happiness level. Having a third child drastically reduces happiness.

As a robustness check of the analysis, the authors addressed the crucial question of possible reversed causation :

Second, we considered dynamic panel data models which take into account the possibility of reverse causation. The positive association between childbearing and happiness could be driven by the fact that happiness increases the probability of having a child, rather than the process of having a child increasing happiness. We first used a simple and intuitive check to test whether past happiness confounds the association between childbearing and current happiness by including lagged happiness (up to 3 years) as controls in the models. The results changed only marginally. Third, we used the standard Arellano-Bond dynamic panel models that add both lagged dependent variables to the model and instruments the key regression variables with their own lags to account for reverse causality (Arellano and Bond 1991). We considered various specifications of lag structures and results were nearly identical to those obtained without the dynamic structure.

In commenting on their figures, I note that Figure 1 gives the happiness trajectory for the German and British samples. They show a substantial decline of happiness after the first-child birth, except when using fixed-effects models, which control for fixed characteristics (i.e., confounding factors such as personality) of the subjects :

The longitudinal fixed-effects approach has several important advantages over cross-sectional research. First, the approach is based on observing individual happiness trajectories over time, allowing us to analyze anticipation, short-term, and long-term changes in happiness with respect to a birth. Second, the approach allows controlling for individual-specific, time-invariant unobserved characteristics, such as personality or genetic endowments, and eliminates the problem of selection into parenthood on happiness. Third, it allows observing the pattern of changes in life satisfaction while controlling for other changing factors, such as age, time, employment or marital status.

All the following graphs use fixed-effects. Nonetheless, there is a bad apple. In figure 3B, for the old parents (35+) there is no increment in happiness for women in the German sample for the years after the first-child birth. It dropped to the initial levels (3-5 years before the birth). For old German men, happiness remains high. In Figure 5, German women with high education show no gains in happiness in the long run. There is no graph for the British sample, but the authors explained it’s because the graphs looked very similar. Given this, women in both the British and German samples don’t feel more happy with children, irrespective of education and age. In this case, an explanation is needed. I believe that having a child would force the women to take care of the children by sacrificing some of her time, notably, their career. They feel less free, so to speak. The men feel more happy than women because they were not sacrificing themselves as caregivers.

All this considered, what kind of variable did they use ? This is the crucial question. And here, we read :

Our key outcome is the subjective well-being of parents. In the German sample, respondents were asked annually, “How satisfied are you with your life, all things considered?” Responses range from zero (completely dissatisfied) to ten (completely satisfied). In the British sample, parental well-being is measured with two questions. The first measures general happiness and is based on the question "Have you recently been feeling reasonably happy, all things considered?" with responses ranging from one (much less happy than usual) to four (more happy than usual). The other question is "How dissatisfied or satisfied are you with your life overall," with answers ranging from one (not satisfied at all) to seven (completely satisfied).

This is the same kind of question formulated in the GSS. And perhaps that’s exactly where the problem is. The way we phrase the question is extremely important and could have a great impact on how people interpret, think about the question. Daniel Kahneman (2006) explains what he calls the focusing illusion :

When people consider the impact of any single factor on their well-being -- not only income -- they are prone to exaggerate its importance; we refer to this tendency as the focusing illusion. Income has even less effect on people’s moment-to-moment hedonic experiences than on the judgment they make when asked to report their satisfaction with their life or overall happiness. These findings suggest that the standard survey questions by which subjective wellbeing is measured (mainly by asking respondents for a global judgment about their satisfaction or happiness with their life as a whole) may induce a form of focusing illusion, by drawing people’s attention to their relative standing in the distribution of material well-being. More importantly, the focusing illusion may be a source of error in significant decisions that people make. (4) ...

Evidence for the focusing illusion comes from diverse lines of research. For example, Strack and colleagues (5) reported an experiment in which students were asked: (i) “How happy are you with your life in general?” and (ii) “How many dates did you have last month?” The correlation between the answers to these questions was -.012 (not statistically different from 0) when they were asked in the specified order, but the correlation rose to 0.66 when the order was reversed with another sample of students. The dating question evidently caused that aspect of life to become salient and its importance to be exaggerated when the respondents encountered the more general question about their happiness. Similar focusing effects were observed when attention was first called to respondents’ marriage (6) or health (7). One conclusion from this research is that people do not know how happy or satisfied they are with their life in the way they know their height or telephone number. The answers to global life satisfaction questions are constructed only when asked (8), and are therefore more susceptible to the focusing of attention on different aspects of life. ...

Individuals who have recently experienced a significant life change -- e.g., becoming disabled, winning a lottery, or getting married -- surely think of their new circumstances many times each day, but the allocation of attention eventually changes, so that they spend most of their time attending to and drawing pleasure or displeasure from experiences such as having breakfast or watching television. (10) However, they are likely to be reminded of their status when prompted to answer a global judgment question such as, “How satisfied are you with your life these days?” ...

With regard to income-happiness relationship, day-to-day happiness is not associated with income but ratings of anger/hostility and anxious/tense are correlated positively with income. Kahneman’s explanation for this intriguing finding was :

Finally, we would propose another explanation: as income rises, people’s time use does not appear to shift toward activities that are associated with improved affect. Subjective well-being is connected to how people spend their time. ... People with greater income tend to devote relatively more of their time to work, compulsory non-work activities (such as shopping and childcare) and active leisure (such as exercise), and less of their time to passive leisure activities (such as watching TV). On balance, the activities that high-income individuals spend relatively more of their time engaged in are associated with no greater happiness, on average, but with slightly higher tension and stress.

In other words, my findings, such as many others, that income is associated with happiness is illusory. And this explains why the “general happiness” question is not accurate in measuring one’s happiness. When they are asked, the respondents probably think about the rare, salient and most important events in their life, what they believe to be the most essential things to achieve in life : marriage, children, job promotion, school graduation. As they realize they achieved them, they would magnify them. But if each of them is associated with daily stress and less attractive activities, the most likely explanation is that success, marriage and children decrease happiness. They overlook the stress they experience every day when they are reminded about their status, which is actually the case when answering the question of general happiness.

The focusing illusion hypothesis can explain why we see a large increase in happiness some few years before the 1rst child is born, which is the expectation of childbirth. Can it account for the increments in happiness in the years following the birth as compared with the years before the birth ? Obviously. The relevant question now is how people allocate their free time. I believe people with no children are more “free” so to speak. There are certainly some reasons why high-SES people have less children than low-SES people, besides the explanation that contraception is more of use among high-SES people. Probably the same reasons why high income tends to decrease happiness overall. All this considered, the main weakness of this longitudinal study is that they have used a poor measure of happiness.

When analyses using day-to-day happiness measures are done, as Powdthavee (2009) summarizes, we see that parenthood is associated with less happiness. Cross-sectional analyses are not the best tools, but whatever the case, it illustrates well why parents focus so much on rare good events by unconsciously thinking that it does much more to compensate for the stress experienced every day :

Why do we have such a rosy view about parenthood? One possible explanation for this, according to Daniel Gilbert (2006), is that the belief that ‘children bring happiness’ transmits itself much more successfully from generation to generation than the belief that ‘children bring misery’. The phenomenon, which Gilbert says is a ‘super-replicator’, can be explained further by the fact that people who believe that there is no joy in parenthood – and who thus stop having them – are unlikely to be able to pass on their belief much further beyond their own generation. It is a little bit like Darwin’s theory of the survival of the fittest. Only the belief that has the best chance of transmission – even if it is a faulty one – will be passed on.

This makes perfect sense. Maybe this phenomenon can also explain why high income is associated with general (illusory) happiness. Because income is associated with higher reproductive success, we might be evolutionarily “conditioned” to believe that income is always a positive outcome while in fact it’s just the opposite.

(Note : When the effect of a predictor, such as Wordsum and Polviews here, is extremely small, we may want to remove that independent variable, so that the sample size will be larger.)

SPSS syntax for GSS analysis :

RECODE happy (1 thru 2=1) (3=0) INTO Happy_Dichotomy.
RECODE race (1=2) (2=1) (ELSE=SYSMIS) INTO BW.
RECODE health (1=4) (2=3) (3=2) (4=1) INTO good_health.
RECODE childs (0=0) (1=1) (2=2) (3=3) (4 thru highest=4) INTO NUMBER_CHILDREN.
RECODE MARITAL (1=2) (5=1) (ELSE=SYSMIS) INTO MARITAL_STATUS.
COMPUTE CHILDREN_AND_MARITAL=NUMBER_CHILDREN*MARITAL_STATUS.
COMPUTE wtssall_oversamp=wtssall*oversamp.
COMPUTE SQRTrealinc=SQRT(realinc).
VARIABLE LABELS SQRTrealinc ‘square root of R income in constant dollars’.

IF good_health=1 ghealth1=1.
IF good_health=2 or good_health=3 or good_health=4 ghealth1=0.
IF good_health=2 ghealth2=1.
IF good_health=1 or good_health=3 or good_health=4 ghealth2=0.
IF good_health=3 ghealth3=1.
IF good_health=1 or good_health=2 or good_health=4 ghealth3=0.
IF good_health=4 ghealth4=1.
IF good_health=1 or good_health=2 or good_health=3 ghealth4=0.

DESCRIPTIVES VARIABLES=age year good_health COHORT WORDSUM SEI realinc SQRTrealinc POLVIEWS health ATTEND
/SAVE
/STATISTICS=MEAN STDDEV MIN MAX.

FREQUENCIES VARIABLES=Zsei Zrealinc SQRTrealinc ZSQRTrealinc Zgood_health Zcohort Zage Zyear Zwordsum Zpolviews Zattend
/FORMAT=NOTABLE
/HISTOGRAM NORMAL
/ORDER=ANALYSIS.

WEIGHT BY wtssall_oversamp.

USE ALL.
COMPUTE filter_$=(BW=1).
VARIABLE LABELS filter_$ ‘BW=1 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN MARITAL_STATUS
CHILDREN_AND_MARITAL
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

WEIGHT BY wtssall.

USE ALL.
COMPUTE filter_$=(BW=2).
VARIABLE LABELS filter_$ ‘BW=2 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN MARITAL_STATUS
CHILDREN_AND_MARITAL
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend ghealth2 ghealth3 ghealth4 ghealth1 NUMBER_CHILDREN MARITAL_STATUS
CHILDREN_AND_MARITAL
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

USE ALL.
COMPUTE filter_$=(BW=2 and Zsei<=0.5).
VARIABLE LABELS filter_$ ‘BW=2 and Zsei<=0.5 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN MARITAL_STATUS
CHILDREN_AND_MARITAL
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

USE ALL.
COMPUTE filter_$=(BW=2 and Zsei>=0.5).
VARIABLE LABELS filter_$ ‘BW=2 and Zsei>=0.5 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN MARITAL_STATUS
CHILDREN_AND_MARITAL
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

USE ALL.
COMPUTE filter_$=(BW=2 and MARITAL_STATUS=1).
VARIABLE LABELS filter_$ ‘BW=2 and MARITAL_STATUS=1 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

USE ALL.
COMPUTE filter_$=(BW=2 and MARITAL_STATUS=2).
VARIABLE LABELS filter_$ ‘BW=2 and MARITAL_STATUS=2 (FILTER)’.
VALUE LABELS filter_$ 0 ‘Not Selected’ 1 ‘Selected’.
FORMATS filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE.

LOGISTIC REGRESSION VARIABLES Happy_Dichotomy
/METHOD=ENTER sex Zage Zcohort Zwordsum Zsei Zpolviews Zattend good_health NUMBER_CHILDREN
/CONTRAST (NUMBER_CHILDREN)=Indicator(1)
/CONTRAST (good_health)=Indicator(1)
/CLASSPLOT
/PRINT=GOODFIT CORR ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).

WEIGHT OFF.

FILTER OFF.
USE ALL.
EXECUTE.

References.

1. Kahneman (2006). Would You Be Happier if You Were Richer: A Focusing Illusion.

2. Kanazawa (2004). Social sciences are branches of biology.

3. Myrskylä & Margolis (2012). Happiness: Before and After the Kids.

4. Powdthavee (2009). Think having children will make you happy?.