Other empirical studies on the ABCT

My earlier post on the empirical evidence of the ABCT was already too long. In this article, I will only add the discussion on the studies not covered earlier. I do not want to post another article each time a new study is released. I will update this article little by little. The evidence is still in favor of the ABCT.

(Last update: February 2015)

1. A short note on the variables used to test the ABCT.

Econometric studies usually understand that the key point of the ABCT is the deviation of the natural interest rate(s) from the market rate(s). Whether there is only one or many natural interest rates is a rather irrelevant debate. Two measures are commonly used. One is the term spread, expressed as the difference between short and long-term rates (see Keeler, 2001; Mulligan 2006; Anker, 2011; Bismans & Mougeot, 2009). The other is the savings-consumption ratio (Carilli & Dempster, 2008; Selleby & Helmersson, 2009).

Most likely, many economists have heard about Hayek’s Prices and Production (1931), and the book is usually cited. But rarely do I see Hayek’s Profits, Interest and Investment (1939) being cited. Hayek’s later works seem under-appreciated. This is regrettable because they were the most relevant. For example, Hayek (1939, pp. 15-16, 27-29, 32-33, 64) explained that what affects the tendency to produce with less or more capital is the shift in the position of the profit schedule but not in the interest rates. More significantly, even when the interest rate fails to rise at the late stage of the boom the employment in capital-intensive industries experiencing a fall in the demand for their products must decline due the rise of the rate of profit on short as compared with that on long investments which induces entrepreneurs to divert whatever funds they have to invest towards less capitalistic machinery. Here are the relevant passages :

If, by keeping the rate of interest at the initial low figure, marginal profits are also kept low, this will only have the effect of a reduction in cost, that is, it will raise the figure at which the supply of and the demand for final output will be equal; but it will not affect the tendency to produce that output with comparatively less capital, a tendency which is caused, not by any change in the rate of interest, but by the shift in the position of the profit schedule.

...

If the rate of interest had been allowed to rise with the rate of profit in the prosperous industries, the other industries would have been forced to curtail the scale of production to a level at which their profits correspond to the higher rate of interest. This would have brought the process of expansion to an end before the rate of profit in the prosperous industries would have risen too far, and the necessity of a later violent curtailment of production in the early stages would have been avoided. But if, as we assume here, the rate of interest is kept at its initial level and incomes and the demand for consumers’ goods continue therefore to grow for some time after profits have begun to rise, the forces making for a rise of profits in one group of industries and for a fall in the demand for the products of another group of industries will become stronger and stronger. The only thing which can bring this process to an end will be a fall in employment in the second group of industries, preventing a further rise or causing an actual decline of incomes.

...

So far our main conclusion with respect to the rate of interest, rather borne out by recent experience, is that we might get the trade cycle even without changes in the rate of interest. We have seen that if the rate of interest fails to keep investment within the bounds determined by people’s willingness to save, a rise in the rate of profit in the industries near consumption will in the end act in a way very similar to that in which the rate of interest is supposed to act, because a rise in the rate of profit beyond a certain point will bring about a decrease in investment just as an increase in the rate of interest might do.

When talking about the possibility of capital reswitching, in The Pure Theory of Capital (1941, pp. 388-389), Hayek stated once again that it is not the interest rate that governs the profitability of the various methods of production and the proportional amount of capital, but the relations between different prices and the shape of the profit schedule (or investment demand schedule) as determined by these price differences. Despite this emphasis on the rate of profit, Hayek (1939, pp. 65-66; 1941, pp. 355-356) seems to admit that the separation between interest rate and profit rate may not be so dramatic in the real world because both variables are likely to be highly correlated. Still, Hayek would have opted for the rate of profit.

Several researchers (Mulligan, 2005; Selleby & Helmersson, 2009; Bjerkenes et al., 2010; Lester & Wolff, 2013; Luther & Cohen, 2014) rely on Garrison’s (2001, 2004) representation of the hayekian triangle. Garrison affirms that the middle stage must suffer some sort of bottleneck. During the expansion, the resources are drawn away from the middle stages, and they will be oriented toward late and early stages, but more toward early stages.

But it is not even true that Garrison’s presentation sounds correct. Huerta de Soto (2009, pp. 379, 502) cited Skousen on the fact that in recession the industrial stages furthest from consumption experience the largest price decline, following by the intermediate stages, and then by wholesale prices, and finally it’s the price of consumer goods that shows the less decline. Skousen discovered during the period 1976-1992 the prices of products from the stages furthest from consumption varied from +30% to -10%, the prices of intermediate goods only oscillated between +14% and -1%, and the prices of final consumer goods varied from +10 to -2%. If the intermediate stages of production were expected to be less affected by monetary policy shocks, one would wonder why the prices of final consumer goods, but not intermediate goods, are the ones that oscillate less, and why the industries of intermediate stages do not have the least price declines. Ramey (1989, Tables 7 & 8) examined the seasonally adjusted quarterly data from 1960 to 1984 regarding several durable-goods manufacturing. A close look at the own-price elasticities for materials “m”, goods-in-process “g”, and finished goods “f” as well as labor “w” in four industries, i.e., primary metals, fabricated metals, nonelectrical machinery, electrical machinery, estimated for 1984, reveals that in each industries, materials have less elasticities, goods-in-process have more elasticities, and finished goods the most. In the estimation of output elasticities for 1984, materials constantly have the smallest elasticities in all four industries, although goods-in-process have (modestly) more elasticity than finished goods. So, the inventories further from the final consumption stage have more instability.

The choice of money supply is also important. According to austrians, a wise definition of money is the so-called True/Austrian Money Supply (TMS/AMS), formulated as TMS = standard money held by the public (notes and coins) + money substitutes. M1, M2, M3, and MZM include different substitutes (for a summary, see this table from Wikipedia). Salerno (1987) and Shostak (2000) explain that each of these measures have their own flaws. For example, M2 and M3 include Money-Market Deposit Accounts (MMDA), which is an investment in various money market instruments. In other words, only the ownership of money has changed. But not the total amount of money. Including it into the definition of money is doing a double counting. Shostak (2000) also says that MZM does not take account MMDA but instead it includes assets that can be converted into money, i.e., all money market (mutual) funds (MMF or MMMF). These various forms of investments are in fact credit transactions. MZM tells nothing about where money is located or what it is, and thus does not distinguish between a claim and credit transaction. Unlike the common measures of money supply, TMS does not include MMDA, MMF, or travelers’ checks but considers the government demand deposits and note balances, as well as demand deposits of foreign banks and institutions.

To illustrate, Selleby & Helmersson (2009) shows that M0 (more liquid) and M4 (less liquid) measures of money supply positively and negatively affect consumption/investment ratio, respectively. Sechrest (2004) compares the correlation of M1, M2, and the austrian measure of money supply with, successively, industrial production, business equipment production, commercial and industrial loans, price levels. There is a modest difference in r² but since it is not an effect size, the r should be used. In this case, there is no difference at all. One must be careful with such interpretation however. Sechrest’s analysis, as he admitted, was purely correlational, whereas most (if not all) econometric studies on the ABCT are causational. For example, Sechrest has not attempted to detect non-stationarity (e.g., through unit root tests) and this is a sine qua non condition for correct causal inferences in time series regression. Also, Shostak (2000) shows that the difference in trends (growths) between M2, M3, MZM and AMS, is serious enough. He finally argues that the soundness of a definition of money supply cannot be established by means of a statistical analysis but only by means of its theoretical soundness.

One very serious problem is related to the classification of industries into late, middle and early stages. Murphy et al. (2010) focused on this issue. Mulligan (2002) has provided perhaps one of the most illustrative examples of this problem. He uses VECM (Table 3) to show how the employment rate reacts to the interest rate. It was found that manufacturing (Mfg.), construction (Con.), finance, insurance, and real estate (Fin.), government (Gov.), and services (Svs.), belong to the early stages of production, and that mining (Min.), transportation and utilities (Trns.), retail trade industry (Ret.), and wholesale trade industry (Whl.) belong to the late stages of production. Mulligan explains this result as follows :

If any sector could be identified a priori as early stage of production, it would be mining. However, many high-value mining activities like petroleum production and field services are clearly late stages, temporally if not conceptually. If less aggregated employment data were readily available for mining, it would be possible to test whether this accounts for the late-stage finding and whether the data confirm that refining is later-stage than mining strictly defined. Mining consists of slow and fast activities, just as slow-growing trees represent higher-order, earlier-stage production, and fast-growing trees are lower-order and late-stage. For example, coal may be delivered and burned to heat homes relatively quickly after being mined, with a minimum of intermediate processing, which would constitute late-stage production. The same mine could also produce coal for steel mills and other sophisticated concerns that use the coal in complex and time-consuming industrial processes, a form of early-stage production. Thus the same production can be either early or late stage depending on whether the output is sold to a final consumer or another firm. It may simply be that fast, late-stage mining activities predominate, or, because labor data is examined here, that fast mining activities are merely more labor intensive.

A further possibility may be that when interest rates fall due to credit expansion, mining concerns find it easier to work existing infrastructure to capacity and possibly beyond, increasing both output and labor employment, than to expand the infrastructure. If this were the case, mining firms would act more like late-stage producers, even while producing primarily in early stages. Their behavior would be atypical and largely attributable to the circumstance that the primary way to expand early-stage mining operations would be to construct new mines, not expand existing ones.

We agree that classification can be rendered difficult due to the final use of these goods. Young (2012) proposes to classify the industries by their degree of roundaboutness, a measure he calls TIOR, calculated by the ratio of total gross output to gross output at a given stage, while total gross output is given by the ratio of gross output at a given stage to the sum of gross output up to that stage.

Another point that needs to be discussed is relative prices. Several economists believe it is not the central point of the theory, either explicitly (Keeler, 2001; Bismans & Mougeot, 2009; Bjerkenes et al., 2010) or implicitly (Anker, 2011). When the assumption about relative prices has been studied, it turned out to be true in some instances (Wainhouse, 1984; Bocutoğlu & Ekinci, 2010; Young, 2012) but wrong in most cases (Bismans & Mougeot, 2009; Bjerkenes et al., 2010; Anker, 2011; Lester & Wolff, 2013; Luther & Cohen, 2014). Garrison (1991, pp. 92, 96-97), Keeler (2001, p. 334) but also Bismans & Mougeot (2009, pp. 247, 254) express their doubt about any theories for which the fundamentals are based on relative prices. It may not be a variable worth studying.

2. Empirical studies.

1. Austrian persistence? Capital-based business cycle theory and the dynamics of investment spending (Michael R. Montgomery, 2006)

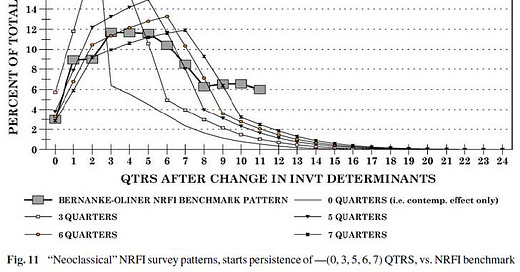
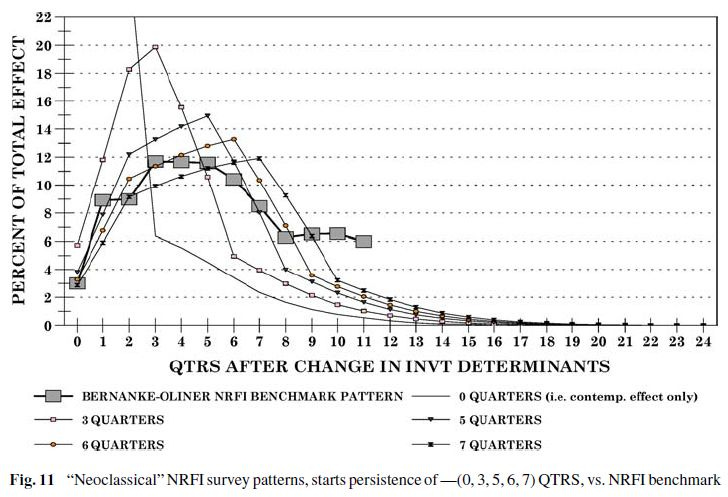
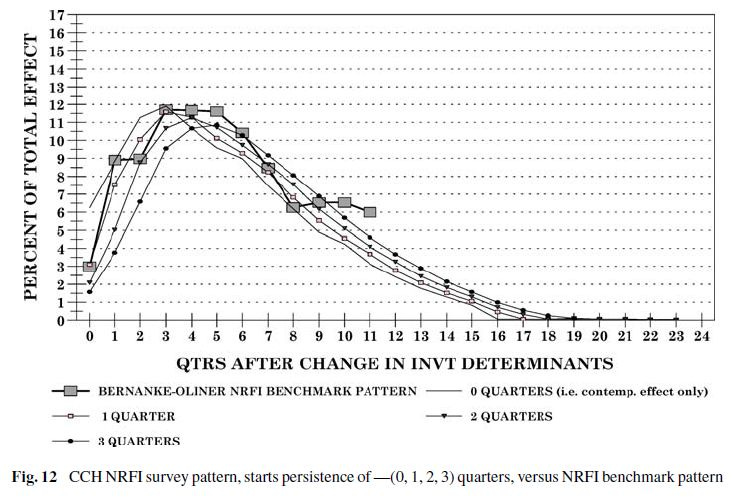
Montgomery (2006) attempts to fit the neoclassical model and austrian model to the data on investment-spending lags. Montgomery (1995) explained in these terms : “Construction cycles of large capital projects trigger later construction cycles of smaller complementary projects. A factory started today requires the production of new equipment months from today. A distribution center started today implies a future need for several new retail outlets. In general, capital produced at one point in time frequently requires additional capital later, and it may be convenient to postpone construction of the additional capital (if its construction period is shorter) so that it is available only when needed.” (p. 188). The author considers the pattern is more complex than the time-to-build mechanism assumed by the neoclassicals. Unlike neoclassical, the austrian model predicts an interaction between structures and equipment spendings, because of their complementarity. He coined the term CCH, capital complementarity hypothesis. He explains (pp. 24, 31) why the neoclassical model is unlikely to show adequate fit to what he calls the (“starts”) persistence of investment expenditures, and which is the long drawn-out response over time by investment spending to changes in its determinants (e.g. interest rates).

The data come from the U.S. Department of Commerce, Construction Statistics Division (CSD) which has conducted occasional surveys of the pace at which nonresidential construction projects progress toward completion following the start of their construction. The CSD defines “start” to mean the physical start of construction, i.e., “groundbreaking”. The first survey was over the 1961-65 period, while the most recent covered 1990-91. With planning lags added, “start” means the date when active, non-contingency project planning begins. And this is the definition chosen by Montgomery.

Given Figures 11 & 12, it seems clear that the econometric benchmark, which serves as point of reference, is closely matched by the austrian (but not neoclassical) model.

Table 3 tells the same story. Montgomery computes goodness of fit measures, which serve to evaluate model’s approximation to the data, such as, the sums of absolute values of deviations (SAVD) and sums of squared deviations (SSD) for each model comparison. The lower the value, the better. Part 1 in Table 3 compares the econometric benchmark pattern with the structures-survey patterns. From Parts 2 & 3, it can be seen that the neoclassical model has lower fit values at quarter 6th, meaning that it suggests 6 quarters of starts persistence, while the austrian model has lower fit at quarter 1st and has also the lowest fit values at quarters 0, 1, and 2 than either of other model comparison regardless of how much starts persistence is assumed. Certainly, the study does not provide any proof that the ABCT fits the data on business cycles. But, at the very least, it shows that the concept of capital heterogeneity must be taken seriously. This is the cornerstone of the austrian theory of capital. It is useful for what follows.

2. Reallocating labor to initiate changes in capital structures: Hayek revisited (Andrew T. Young, 2005)

Young (2005) studies job reallocation (percent of total jobs) on quarterly data, 1972:2 to 1993:4. The panel includes 20 two-digit SIC for the US manufacturing industries. Job creation plus job destruction equals total reallocation (R). The federal funds rate (FFR) is obtained from the FRED database. The variable of interest (desired reallocation) is the FFR observed at an earlier date. Specifically, it is FFR (also denoted r) at t-1 because any given firm can only observe FFR at t-1.

The |r_t-1-r_t-2|=|Δr_t-1| captures an asymmetric effect of policy on reallocation. While any specific capital structure is only realized with a lag, the desired reallocation to initiate and carry out the structure will be reckoned immediately. |Δr_t-1| is the latest signal available to firms of policy stance changes.

The other variables are denoted R, for total reallocation, NEG for job destruction, and POS for job creation. The subscript t-1 denotes the lagged values of a given variable. The regression models include the lagged values of the dependent variable (e.g., R_t-1, NEG_t-1, POS_t-1), as well as |Δr_t-1|, and a dummy variable, W, which is a set of unobservables relevant to the firm’s decisions. The dependent variables are, successively, R, NEG, and POS. The parameter λ is the lagged values of the dependent variable, which is considered by Young as the speed of adjustment. The parameter α is the effect of one unit increase in desired reallocation on the dependent variable.

Quantitatively, the effects on reallocation are not economically large. The standard deviation of reallocation is 3.556%. The estimate of α is 0.391. So a standard deviation change in the federal funds (negative or positive) is associated with a change in desired reallocation of about 11% of its standard deviation.

To arrive at this value of 0.11, Young divided the raw estimate of the (IV) independent variable (0.391) by the standard deviation of the (DV) dependent variable (3.556). This is the Y-standardized coefficient. But to convert the unstandardized (raw) regression coefficient to a fully standardized coefficient, one must proceed as follows : coefficient(IV)/(SD)DV*(SD)IV. The correct operation is 0.391/3.556*1.330=0.146. This correlation is modest, but not small. The real effect size is 14%, not 11%. The parameter estimates for |Δr_t-1| when the DV is NEG and POS are, respectively, 0.436 and -0.042, which give standardized coefficients of 0.436/3.556*2.736=0.335 and -0.042/3.556*2.331=-0.027. Young finally performs VAR models and found that the contribution of monetary policy on the variance decomposition in manufacturing reallocation is just below 10%. In conclusion, the response of desired reallocation (to ΔFFR) is about 10-14% of a standard deviation of the reallocation rate. Young concludes this is a positive, but modest support for the ABCT.

Murphy et al. (2010) criticized Young (2005) on several grounds. Using the same data and method, they report different estimates. Young’s were 0.819 and 0.391 but Murphy’s (2010) were 0.156 and 0.544. This means the effect size of |Δr_t-1| is not 14% anymore, but 20%, using the above computation, and that the effect of this variable of desired reallocation is stronger than the lagged values of changes in FFR. Unfortunately, neither Murphy et al. (2010) nor Young (2011) explain the reason for this divergence. In any case, another criticism concerns aggregation problems. The dummy variable W is assumed to be the same in all firms in a given industry. This means that these firms’ decisions rely on the same set of unobservables. They write : “It is true that he allows the magnitude of W to differ among firms in the same industry by an error term - ε_it, but his assumption is that every firm; i.e., each decision maker, bases his decision on the same set of (unobservable) variables”. They argue this is not an assumption made in the ABCT. But Young probably did almost all that is possible given the nature of the data. The condition considered by Murphy et al. (2010) seems extremely difficult to fulfill. A further problem is that all the industries in the sample come from the manufacturing sector. According to them, this was the worst sector to pick because credit expansion has the smallest effect on the middle stages. But contra Murphy, it is not true that intermediate stages are the least affected by monetary shocks (see de Soto, 1998 [2009], p. 502). This aside, Young (2011) replies “In the real world manufacturing occurs at various stages of production, e.g., drills are manufactured to extract iron that is manufactured into assembly lines that are then used to manufacture cars.” (p. 23). Murphy et al. (2012) respond that in this case, Young should have abandoned his earlier classification. Murphy is probably right about classification, as Mulligan (2002) shows that manufacturing is probably an intermediate stage. Given the ABCT’s prediction, a negative (positive) correlation between employment rate and interest rate was interpreted as indication of early (late) stage, and manufacturing indeed had a negative sign for all maturities (3-months to 5-years) but none of the coefficients were significant, which can be meant that manufacturing is not better characterized as early stage either. Perhaps intermediate stage, indeed.

3. The Time Structure of Production in the US, 2002–2009 (Andrew T. Young, 2012)

Young (2012) decided to circumvent the usual criticism made by austrian economists, e.g., that the empirical classification of early, middle and late stages of production suffers from subjectivity. He takes the examples of seashells. If sold by the seashore, they can be considered as primary goods but these seashells are also very close to their consumption good form. This makes classification relatively ambiguous. He then develops a new measure of roundaboutness :

The proposed metric is an industry’s total industry output requirement (TIOR). The TIOR is, for a given industry, “the output required, both directly and indirectly, by each [other] industry to deliver a dollar of final demand of industry output to final users.” In other words, it is the amount of gross output from other industries that must be produced per dollar of a given industry’s output: the ratio of total gross output to final output for an industry. This ratio will be greater than unity by definition. The critical assumption of this study is that an industry’s roundaboutness is proportional to its TIOR.

Young collects TIORs for 65 industries for the years 1998 through 2009 from the BEA data, although the final analysis involves 85 time series observations for 20 industries. The ten most and ten least roundabout industries are defined given base year 2002. The average annual value-added growth rate for each sample is then calculated for each year, 1999 to 2009. The patterns of value-added growth for more and less roundabout industries are compared to one another with the predictions of ABCT.

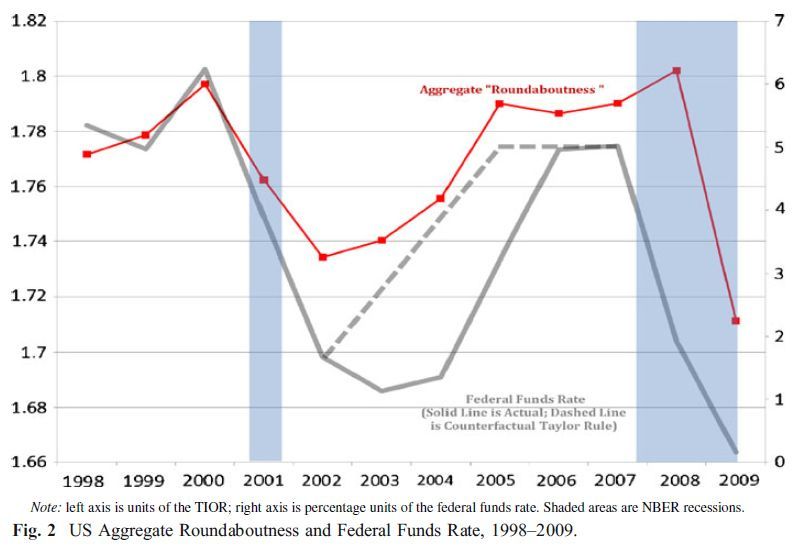
He also constructs an aggregate roundaboutness measure for the US economy for each year, 1998 to 2009, by taking a weighted sum of industry TIORS where the weights are industry shares of total value-added. This allows him to see if the aggregate structure of production has changed over time (2002-2009).

Table 2 shows that the TIOR increases with the number of stages, gross output, and total gross output (the sum of gross output of each stage). The TIOR is calculated as the ratio of total gross output to gross output. The longer the process, and the more it is roundabout. Table 3 shows that 7 industries are present in both the 1998 and 2009 most roundabout groups, and 6 industries are present in both least roundabout groups. The correlation of 1998 and 2009 rankings is 0.847.

Figure 2 shows that the aggregate roundaboutness moves in a manner consistent with the ABCT. Figure 3 shows that the average (nominal) annual value-added growth for the more roundabout (MR) increases and declines more than for the less roundabout (LR) industries. Figure 4 shows that the PPIs for the MR industries rise (drop) during the boom (bust) while the PPIs for the LR industries are stagnant. The MRs started to become more roundabout when in 2002 the Fed began its expansionary policy (given Taylor rule). By 2004, among MR industries, PPI increases more than the value-added growth (15.6% vs 11.7%). The huge pike in PPI for MRs was unexpected. Young suspects that “One possible explanation for the 2008 MR inflation is the spike in imported oil prices in 2008. The real price per barrel of imported crude oil was $71.70 in 2007; it rose by 32 percent to $95.17 in 2008 then fell 36 percent to $60.89 in 2009.” (p. 90). This seems plausible because Petroleum & Coal Products was among the MR industries (where PPI inflation jumped from 24.8 percent in 2007 to 68.9 percent in 2008). In addition, oil is an important input to other MRs, e.g., Primary Metals, Water Transportation, Plastics & Rubber Products, that have seen an inflation spike in 2008.

Despite its originality, the study needs to be replicated. Some industries (notably, LR) did not have data for all years.

4. The Empirical Relevance of the Mises-Hayek Theory of the Trade Cycle (Lester & Wolff, 2013)

Lester & Wolff (2013) examine the data Federal Reserve Board (FRB). The variables in question were the monthly observed federal funds rate (FFR) data from the FRB H.15, and industrial production from FRB G.17. The time span is from 1972 to 2011 (all data available at a monthly frequency). The groups for industrial production are : crude, primary, semi-finished, and finished. As the semi-finished and primary are almost perfectly correlated, they use primary as the measure of intermediate goods production. They analyze the behavior of PPI on finished goods, intermediate goods, and crude goods. The PPI ratios (for commodity prices) used are Crude/Intermediate PPI and Finished/Intermediate PPI. The IP ratios (for industrial prices) used are Crude/Primary IP and Finished/Primary IP. They cite Garrison (2004) for saying “The Hayekian triangle is being pulled at both ends against the middle” and for that reason they expect early and late stages to expand, to the detriment of the middle stage, in response to monetary policy shocks.

Their analytic method involves Structural VARs-derived Impulse Response Functions (IRF). When they test for unit root(s), using Dickey-Fuller, it appears that the variables are integrated of order 1, I(1). Thus, all variables are differenced (to get stationarity) and ready to be used, with any relevant information carried out by levels in variables being lost in this process. But otherwise, spurious regression problems wouldn’t be avoided. In such a case, we could generally apply ECM, after testing for stationarity in cointegration, but the authors were only interested in the changes.

Figure 3 shows the impulse responses for IP and PPI ratios. The crude/primary IP shows a quick drop of 1%. The finished/primary IP shows a drop of 1% during the period of 20-60 months. The crude/intermediate PPI shows an initial drop (period of 0-10 months) of 1% followed by an increase of 2% (period of 10-20 months) and a further gain of 1% more in later periods (20-60 months). The finished/intermediate PPI shows a slight increase (perhaps half a percentage) which is immediately followed by a decline of (probably) 1% during the period 14-60 months. It seems that it is only the crude/primary IP ratio that is incoherent with ABCT, but in general the effects are very small. The large confidence intervals for some estimations suggest that a larger sample size will greatly help to have a clearer picture.

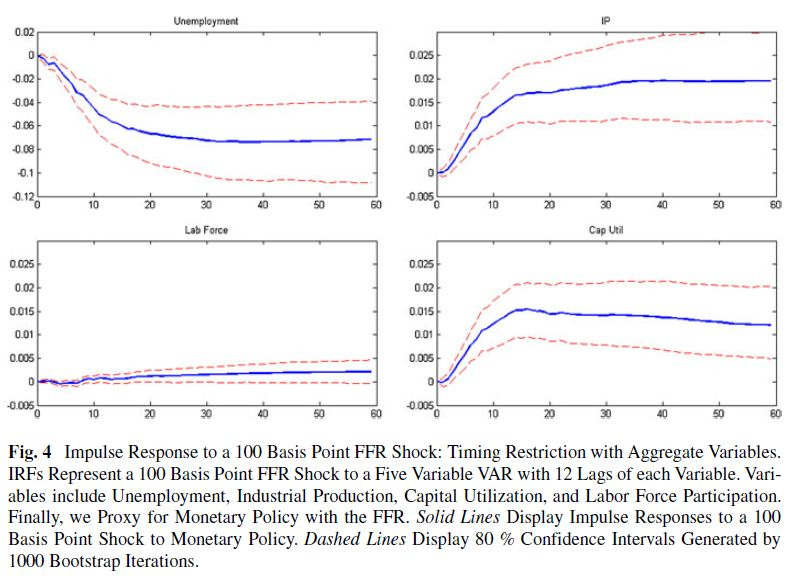
Figure 4 shows other impulse responses to a shock in FFR. For unemployment, there is a large drop (7% or -0.070), a large increase in industrial production (2% or 0.020) and capacity utilization (1.5% or 0.015), but labor force participation barely increases (0.2% or 0.002). This supports the ABCT assumption that more (previously) unused resources are being used in the expansion phase, and that the existing factors (resources) are used more intensively.

They also attempt to replicate their analysis on Figure 3 by using monetary base, M1, M2, and Romer & Romer (2004) date series (instead of FFR) and reach similar conclusions. Figure 5 (monetary base shock) is similar to Figure 3 except that crude/primary IP shows an increase and that crude/intermediate PPI ratio shows an initial decline followed by an almost equal increase in the periods 0-10 and 10-20 months, respectively, while after this period (20 months) there is no detectable trend at all. Figures 6 & 7 are similar to the previous IRFs, except that in Figure 7 (M2 shock) the finished/primary IP and finished/intermediate PPI ratios do not move at all.

Figure 8 shows the industrial production (IP) response to Romer monetary shock. The primary goods production shows the largest gain, followed by finished, and followed by crude. This is totally incoherent with the ABCT. Figure 9 is more coherent with the ABCT. The prices of crude and intermediate goods show a large increase following Romer monetary shock, and finished goods prices increase but are lagging behind. The percent change in prices for crude goods surpasses intermediate goods after 25 months and is 1% larger at 50-60 months.

Finally, they apply Blanchard-Quah decomposition and attempt, again, to replicate their analysis on relative prices. Figures 10-13 show the IRFs for the various monetary measures. Except with FFR, crude/primary IP always shows a quick rise followed by a stability. Finished/primary IP declines when monetary base and M1 are used. Crude/intermediate PPI ratios show the same pattern as displayed in Figures 5-7, except FFR for which there is a steady increase but slight with too large confidence intervals (CIs). Finished/intermediate PPI ratios show a very similar trend as displayed in previous IRFs. Once again, the effect sizes are too small.

The authors conclude that one of the propositions (i.e., resource utilization) of the ABCT is confirmed, but not the other (i.e., relative prices). On the first proposition, one should not conclude that this is a key point of the ABCT. The main reason why more resources are used is related with the decline in “idle” resources, notably unemployment, following (upward) monetary shock. But even when the amount of resources used on aggregate does not change at all, the ABCT effect may occur, because the key point is the relative distortion in the structure of production. ABCT predicts that monetary over-expansion causes the wrong type of investment and goods to be made, not necessarily more inputs and outputs than before. In the real world however, this is very likely to be irrelevant because an expansionary phase is generally accompanied by a lowering of unemployment, which is a sign that more resources are being used. On the second proposition, they believe the ABCT predicts changes in relative prices in favor (disfavor) of early stage (late stage) industries during the boom. In fact, their (negative) result is not surprising given that Bismans & Mougeot (2009) and Anker (2011) failed to confirm the ratio producer/consumer price index to be a relevant factor behind the business cycle but still conclude the data confirms ABCT main predictions because interest rate gaps produce changes in consumption/investment expenditure ratio in favor of the latter. It is thus surprising that Wainhouse (1984) and Young (2012) find a behavior in relative prices consistent with the ABCT.

One potential problem with the study is related to the classification of industries into early, middle, late stage, as noted by Murphy et al. (2010). Young’s (2012) study may help to better understand this problem. But these authors are well aware of this problem as they wrote :

There are, however, several subtle differences. First, the BLS distinguishes between commodities, not the industries that produce the commodities. Second, commodities can appear in more than one category so that each category is a weighted sum of commodities. For instance, gasoline is both a final consumption good and an input for commodity production in some manufacturing industries. Finally, the PPIs reflect the output prices of producers, not their input prices, whereas the Federal Reserve Board’s index for industrial production reflects the production of the inputs for each stage-of-process.

Another problem with the study is the neglect of the interest rate gaps. Other studies (e.g., Carilli & Dempster, 2008) have made explicit that the ABCT relies on the assumption that monetary shocks cause interest rate gaps, which in turn cause resource reallocation and output.

5. An Empirical Analysis of the Austrian Business Cycle Theory (Luther & Cohen, 2014)

Luther & Cohen (2014) faulted Lester & Wolff (2013) for not having tested the ABCT properly. L&W (2013) used the FFR as a measure of monetary policy while L&C (2014) opted for the deviation in the FFR from (an estimation of) the natural rate. The latter is a more relevant variable given that ABCT does not predict lower interest rates to cause the business cycle but that a sustained interest rate level below the natural rate would cause the business cycle. Thus, L&C (2014) replicate L&W (2013) using the same data and statistical methods. They conclude in disfavor of the ABCT.

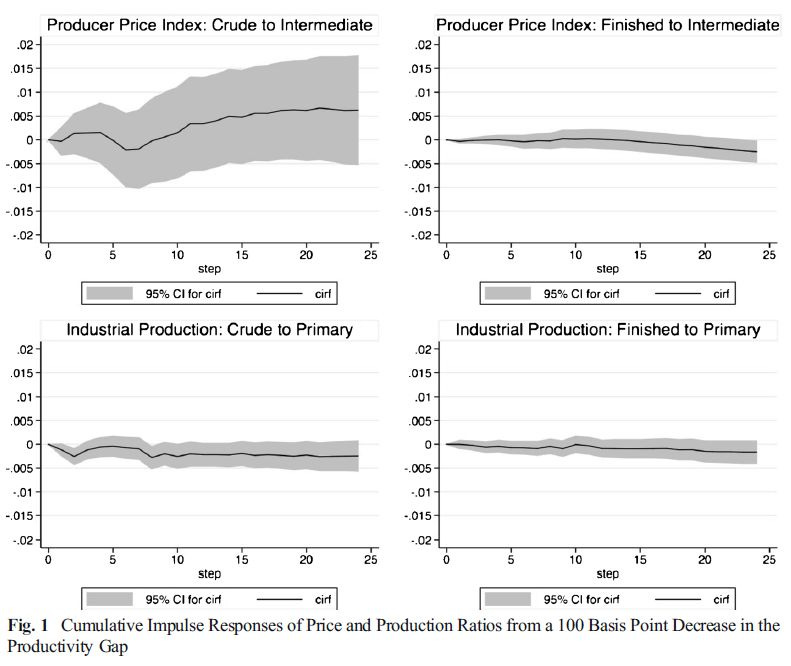
They use 2 measures of interest rate gap. The first measure uses Selgin et al. (2011) measure of natural rate. Selgin et al. (2011), assuming time preference and labor input growth rates are constant, estimate the real natural rate of interest at time t, r_tⁿ as the sum of the long-run real natural rate rⁿ, and the difference between the expected year-on-year total factor productivity (TFP) growth rate at time t, E(g_t), and the mean year-on-year TFP growth rate g. To get the nominal natural rate i_tⁿ they add the year-on-year inflation rate (π_t) calculated from the BEA Personal Consumption Expenditure price index, thus i_tⁿ=r_tⁿ+π_t. Their market rate comes from the monthly effective FFR. The obtained measure of interest rate gap is called productivity gap, hence PG_t=FFR_t-i_tⁿ. The second measure uses Taylor (1993) neutral policy rate. The (nominal) neutral rate can be written as i_t^TR=π_t-1+r*+0.5(π_t-1-π*)+0.5(y_t-1-y*_t-1), where π_t-1 is the year-over-year inflation rate at time t-1, r* is the long run interest rate, π* is the inflation target, y_t-1 is the year-over-year output growth at time t-1, and y*_t-1 is potential output growth at time t-1. Both r* and π* are assumed to be 2%. This neutral rate measure maintains that rates should increase when inflation is above target and/or output growth is above potential. The Taylor gap is computed as follows TG_t=FFR_t-i_t^TR.

They compute the IRFs for crude/intermediate PPI, finished/intermediate PPI, crude/primary IP, finished/primary IP, over 24 months. Figure 1 shows stability for all ratios, except crude/intermediate PPI which increases by about 0.5% in response to a shock in productivity gap. The confidence intervals (CIs) are too large. In Figure 2, the same ratio shows a decline in 0.5% after a shock in Taylor gap with too large CIs. All other ratios again do not show any response at all.

6. On the Empirical Relevance of the Mises-Hayek Theory of the Trade Cycle (Luther & Cohen, 2014)

Luther & Cohen (2014) attempt to replicate their previous study (see above). The authors affirm that their previous findings, as well as Lester & Wolff (2013), do not have the appropriate measures of production and prices. Nor is their present study here. The conclusion from the present study is mixed.

Unlike their previous study, they have data covering 60 months. Figure 4 depicts the IRFs for productivity gap, and it shows that the crude PPI increases by 2% and reacts faster than intermediate and finished PPI which grows by only 1%. The fact that finished PPI grows after crude PPI would also be coherent with the story underlined in the ABCT, where the rising wages in more roundabout industries will sooner or later give rise to an additional spending in consumer goods. With regard to industrial production, the primary and semifinished IP grow by 1% whereas crude and finished IP grow by a mere 0.05%. This is incoherent with the ABCT. Figure 3, depicting IRFs after FFR shocks, shows that crude IP increases by less than other IPs, and that intermediate and finished PPI are more or less constant over time while crude PPI increases by 2%.

7. Austrian Economics: Application on Norwegian Business Cycles (Bjerkenes, H., Kiil, H., & Anker-Nilssen, P., 2010)

Bjerkenes et al. (2010) examine the data from Statistics Norway, quarterly 1978-2010 (with 121 observations). They use time series regressions with the following variables GDP (dependent variable) and M0, INV/CON, E/L Labour, PPI/CPI, YIELD.

E/L Labour is computed as LABOUR_t=L_t^Early/L_t^Late and is measuring the ratio of early stage production relative to late stage production. Early stage is represented by construction, mining, quarrying, while the late stage is represented by business service, post and tele communication, financial intermediation, hotels, and restaurants. YIELD is the yield curve as used by Keeler (2001). A steeper (i.e., positive) curve indicates a greater yield (interest rate) for longer maturity bonds. For short-term interest rate, they choose to look at the three month interbank interest rate (NIBOR3M) and 10 year government bond as the natural rate of interest. INV/CON is given by I/C_t=ln(investment_t/privateConsumption_t). Finally, the variable PRICE defined as ln(PPI/CPI) was used to determine relative prices.

All variables were tested for stationarity. GDP and PPI/CPI have unit root(s). The non-stationary variables are made stationary with the Hodrick-Prescott filter, except for YIELD since it is stationary at level form. The choice of appropriate number of lags is based on model fit indices, such as AIC and SIC.

They perform Granger causality tests for the pairs of variables assumed to be causally related by the ABCT. The number of observations ranges between 111 and 119 (decreasing when lags increase). The causality of MONEY on ΔYIELD, presented in Table 7-4, shows no consistent causal relationship as hypothesized, as indicated by the F-statistics which oscillate between 0.7 and 1.7, most of them between 1.05 and 1.30. There is no reverse causality either, as ΔYIELD does not cause MONEY except at lag=1 for MONEY. The causal relationship of ΔYIELD on LABOUR is established, in Table 7-5, at 1% and 5% level except at lag=2 for LABOUR where it is significant at 10%. There is no reverse causality, as virtually all specifications are non-significant for LABOUR causing ΔYIELD, and only 3 lags reach significance at the 10% level. Table 7-6 shows that ΔYIELD Granger-cause I/C ratio, as most lags reach significance at 5% and 1% level. The absence of reverse causality is suggested by the F-stats showing significance only for the four last lags (i.e., seven to ten lags). According to the authors, “This might be explained as a logical feedback loop where an “artificial” set interest rate affects agents to change their behaviour which in turn affect the same market interest rates” (p. 73). As seen in Table 7-7, ΔYIELD does not cause PRICES, the F-stats range between 0.5 and 1.07. However, PRICES may cause YIELD, 5 specifications show significance, 3 others are significant at 10% level, the remaining 2 specifications are not significant at all. According to the authors, “The causal relationship from PRICES to ΔYIELD could indicate a feedback loop from the price information in the market back to demand-led changes in interest rates. Such feedback loops are not uncommon considering events as overreactions or changing perceptions and expectations due to changes in price levels.” (p. 74).

A correlation matrix of the variables, at different (quarterly) lags, is presented in Table 7-2. The correlation between MONEY and ΔYIELD is positive in early periods, and then becomes negative between quarters 7 and 20, and turns positive again at quarters 22-24. The correlations are meaningful only at quarters 0-2, 12-18, 22-24. The ABCT predicts this behavior, that is, monetary shocks initially cause a steeper yield curve, before a reversal occurs at the end of the expansionary phase. ΔYIELD and LABOUR show initially a null correlation, but increases steadily, peaks at 0.37 at quarter 8, and then diminishes steadily, becoming negative at quarter 18. Only quarters 2-15 show meaningful correlations. This is coherent with the ABCT’s story that a steeper yield curve causes resources to be reallocated toward early stages, but then reverse at the onset of the recession. ΔYIELD and I/C have initially a negative (weak) correlation but increases steadily, reaching 0.57 at quarter 12 and then declines steadily, becoming negative at quarter 21. The correlations are meaningful at quarters 3-18 and 22-24. This pattern is also predicted by the ABCT, since steeper yield curve is supposed to cause higher degree of investment relative to consumption and this trend reverses at the end of the expansionary phase. ΔYIELD and PRICES have an initially low correlation but there is a steady increase in correlation, becomes positive at quarter 3, meaningful at quarter 7, peaks at quarter 11 with r=0.21 and then declines steadily, becomes negative starting at quarter 19. Only quarters 7-15 and 21-24 have meaningful correlations. The pattern confirms ABCT in the sense that it predicts an increasing trend in PPI/CPI ratio at the beginning but a decreasing trend in PPI/CPI ratio at the end.

Table 7-8 shows the intercorrelation between the independent variables. PRICES correlate at 0.3232 and -0.1400 with I/C and LABOUR, respectively, and LABOUR and I/C are correlated at 0.4804.

Their table 7-9 shows that the correlation between PPI/CPI ratio and GDP is positive and increases with lags, until quarters 8-9 where the size of correlation declines, turns negative at quarters 15-16, and stagnates after. The story highlighted in the ABCT was that capital goods production increases relatively more at the beginning of the cycle before a reversal occurs due to a later rise in consumer products when the production of new consumer goods will arrive at a slower pace due to the productive resources in late stages that are being withdrawn and used in early stages (Huerta de Soto, 2009). This is what we see in the data. The correlation between I/C and GDP is positive and strong but declines linearly with lags, becomes zero at quarters 12-13, and becomes increasingly negative after. This is consistent with the idea that I/C positively affects GDP at the beginning of the cycle and negative effect at the end of the cycle. Similar pattern is seen for the correlation between LABOUR and GDP except that it turns negative at quarters 10-11. This, again, fits the story that a higher early/late labour ratio manifests itself at the beginning of the cycle but falls gradually during the cycle.

Table 7-10 shows multiple regression where causal relationships are assumed to be instant (no time lags). The number of observations is 121. There is a significant F-test=20.0610 for the model with Pearson R=0.5828 and R²=0.3227. The PRICES variable has a too large p-value (0.2110). I/C and LABOUR show a positive coefficient. Thus, an increase in GDP can be explained by increased levels of investment/consumption ratio as well as increased ratio of early/late stage labour, and increased ratio PPI/CPI (although the effect size is likely to be weak). With regard to PPI/CPI ratio, the authors noted : “This contributes to justify Mises’ abandonment from the focus where pro-cyclical price movements account for the cycle. Keeler also considers that “there may be no general hypothesis that can be stated about these relative prices during the phases of the cycle”. However, current prices and expectations about future prices act as important market information which affects behaviour during the cycle.” (pp. 81-82).

Due to the difference between sub-periods, a new regression is run for the last two sub-periods (1989-2009, with 81 observations). Table 7-11 shows that the F-value, the Pearson R and R² increase dramatically. I/C ratio has a greater effect than before, but LABOUR has a weaker effect. PRICES variable has probably a weak effect on GDP, once again. To explain the weaker effect of LABOUR, the authors suppose that I/C just accounts solely for most of the variations of GDP in this model.

Why relative prices do not affect GDP meaningfully is a question worth investigating. The authors stated (p. 78) that Norway is an open raw material economy, which makes it sensitive to international disturbances. As a result, Figure 7-5 shows no relationship over time between relative prices and GDP. One would wonder if the reason why relative prices have been found to be weakly related to GDP in previous studies is due to similar reasons.

The conclusion of the authors is surprising. They conclude in favor of the ABCT while in fact their own result suggests a rejection of the theory (although the correlational analyses strongly support the ABCT). As explained by Carilli & Dempster (2008), if the ABCT would be confirmed, each part of the mechanisms must be true. As seen above, M0 does not Granger cause yield. Hasty conclusion is not justified, however. As Selleby & Helmersson (2009) showed, the use of different money aggregates (e.g., M0 versus M4) can produce different results. M0 (a more liquid measure of money) tends to increase consumption/investment ratio while M4 (a less liquid measure of money) tends to decrease the ratio. It would have been more informative to compare the results by using different measures of money supply (see, e.g., Sechrest, 2004). Another possibility is method. As we will see, Russell & Langemeier (2014) report results that depend on the choice of statistical methods.

8. Austrian Business Cycles: From Theory to Empirics (Richard Whittle, unpublished version, 2012)

Whittle (2012) uses the same variables as in Bjerkenes et al. (2010). YIELD_t = ln(1+3monthIBR_t/1+10yearsGovernment_t). INVCON_t = ln(investment_t/consumption_t). RESOURCES_t = output_t^Initial/output_t^end. The data were from the Bank of England statistical services. Stationarity is of crucial importance in time series analyses. The augmented DF and modified DF reveal the variables were all non-stationary (having unit roots). Thus, Whittle uses the Hodrick-Prescott (HP) Filter for detrending the variables.

M0 correlates negatively with YIELD (pearson correlation of -0.272 for 1990-2006 and -0.703 for 1990-1995). A greater M0 is thus associated with a lower ratio short/long term interest rate.

The author then performs a multiple regression, with GDP in dependent variable, and INVCON, M0, YIELD, and RESOURCES in the set of independent variables. Their regression coefficients, respectively, are, 0.0017, 0.3498, -0.1727, 0.4212 with adjusted R² of the model equals to 0.648. Thus, except for investment/consumption ratio, every variable has an effect on GDP in the expected direction. The author argues that INVCON does not predict GDP because GDP was not driven by an effect of private savings but instead by monetary shocks. INVCON has no effect above the effect provided by M0. Selleby and Helmersson (2009) have also analyzed the business cycles in the UK and conclude in favor of the ABCT as well.

9. Austrian Business Cycle Theory: Evidence from Kansas Agriculture (Levi A. Russell and Michael R. Langemeier, 2014)

Russell and Langemeier (2014) use time series data from 1973 to 2010 on Kansas Agriculture. The money at zero maturity (MZM) was obtained from the St. Louis Federal Reserve FRED database. MZM is defined as the M2 money supply with less time deposits plus money market funds. For the output in Kansas agriculture, the annual data on net farm income and value of farm production (gross margin) were used. Output is specified as the ratio of net farm income to value of farm production. This is done to eliminate the effect of prices on output. Following Carilli & Dempster (2008) they use the ratio of savings/consumption as a proxy for the natural interest rate.

Augmented Dickey-Fuller was used to test for presence of unit root. All series were non-stationary in their value levels, and thus the variables were transformed through differencing. The AIC index indicates that the optimal number of lags is 3. They then conduct Granger causality test (Table 3). MZM did not Granger cause interest rate gap (p-value=0.302), but the (lags of changes) interest rate gap did Granger cause agricultural output (p-value=0.053). One problem with Granger’s test is the use of significance test (p-value). It is known that p-value has two components : effect size and sample size. The smaller the sample, the larger the p-value.

An Impulse Response Analysis (IRA) from the SVAR coefficients (Tables 5-6) was conducted. The predictor (impulse) variable was ΔMZM and the response variables were ΔGAP and ΔOUTPUT. The result shows that an exogenous shock (in one unit) to the change in MZM results in a large increase in the change in the interest rate gap (years 1). This change becomes negative at years 4-6 ahead and returns to a positive (albeit small) value in years 7-8. The changes in MZM has, initially a positive impact on ΔOUTPUT, especially at year 4, but turns negative years 6-8. When ΔGAP is the impulse and ΔOUTPUT the response variable, the ΔGAP has no effect on ΔOUTPUT. The confidence intervals are large, which is due to small sample sizes.

The Forecast Error Variance Decomposition (FEVD) gives the percentage of the forecast error variance of a given variable that is explained by exogenous shocks to all the variables over time. The result from the FEVD (Table 7) indicates that ΔMZM is a relatively more powerful predictor of ΔOUTPUT. Nearly all the variation in the forecast errors (ΔMZM, ΔGAP, ΔOUTPUT) is a function of exogenous shocks to the change in ΔMZM. Shocks to the change in the interest rate gap play no role in the variation of the forecast errors for the change in output.

A test of polynomial distributed lag shows (Table 8), that the p-values on the linear and quadratic terms were both extremely significant. This indicates that the relationship between ΔGAP and ΔOUTPUT was nonlinear and could display an inverse U-shaped pattern. The opposite would have disconfirmed the ABCT. The five earliest lags have positive coefficients (not significant at the 10% level) and the final three lags have negative coefficients. Only lags 7 and 8 have point estimates that seriously diverge from zero. Perhaps sample size is problematic. Finally, the Durbin-Watson test indicates white-noise errors. This indicates that the lag length selection is not problematic.

To determine whether one of a pair of variables was better at forecasting a third, they perform a Diebold-Mariano (D-M) test for differences in the forecast errors of two models. The first model is ΔMZM predicting ΔOUTPUT. The second is ΔGAP predicting ΔOUTPUT. A squared loss function was used to compute z-scores to determine if there is a statistically significant difference between the forecasting power of two models. Recursive, pseudo-out-of-sample forecasts were estimated for two different models starting in 1988. The null hypothesis is that the expected value of the difference between the squared errors is zero. At every step, the z-scores indicate no model is better than the other at predicting ΔOUTPUT.

The authors argue that the results overall appear ambiguous. In fact, the evidence for ABCT seems positive, but some people may see it as very equivocal. Because money should have caused an interest gap which would have, in turn, caused output changes. The first (second) mechanism is true (untrue) for IRA and FEVD analyses, and the reverse pattern was observed from Granger test, even though the first mechanism is still apparent from Polynomial Distributed Lag. In other words, the result was highly dependent on the methods.

One of the primary difficulties with this analysis is determining whether MZM is a good indicator of reserves. Part of the problem here is that many Austrian Business Cycle theorists speak of the supply of money rather than reserves as the variable that is manipulated by the monetary authority.

The above is another limitation of the study highlighted by the authors.

10. International Empirical Evidence on the ABC’s of Recessions (Efthymios G. Tsionas, 2014)

This study is probably the first one to look for the international evidence of the ABCT. The data are derived from the IMF’s International Monetary Fund (IFS), in the period 1980:1–2006:4, for USA, Australia, Canada, UK, Japan, Germany, Spain, France and Italy. The number of observations would be 27(years)*4(quarters)=108. The variables of interest are, Gross domestic product, gross fixed capital formation, Credit, Lending Interest Rates, Money Supply. The analysis involves a panel (multiple) regression in the following form :

y_it = β_oi + β_1iI_it + β_2ic_it + β_3ir_it + β_4im_it + u_it

where y_it is output in country i and quarter t, I_it is investment, c_it is credit, r_it is the interest rate, m_it is money supply, and u_it is an error term.

Because stationarity is the basic requirement for all time series regression, the variables are subjected to ADF tests, but also to three panel unit root tests such as IPS, MW, and Choi tests. With regard to ADF, all variables are non-stationary, except money in UK. First-differencing makes them stationary. For the other tests, all variables again are non-stationary in their levels. However, the null hypothesis of unit root(s) can be rejected by first-differencing the time series.

The next step involves a test of cointegration, through the Johansen test. The null hypothesis of at least one co-integration vector is accepted. They also conduct a Pedroni panel cointegration test, and it supports the hypothesis that there is a single co-integration vector irrespective of the dependent variable (output, investment, money supply and credit).

Tsionas uses panel regression with the fully modified OLS (FMOLS) because a standard panel OLS estimator has a distribution that is asymptotically biased and depends on nuisance parameters associated with the presence of serial correlation in the data. But FMOLS corrects for endogeneity bias (i.e., correlation between differences of the regressors and error term). The author also allows for heterogeneity in short-run dynamics via fixed effects.

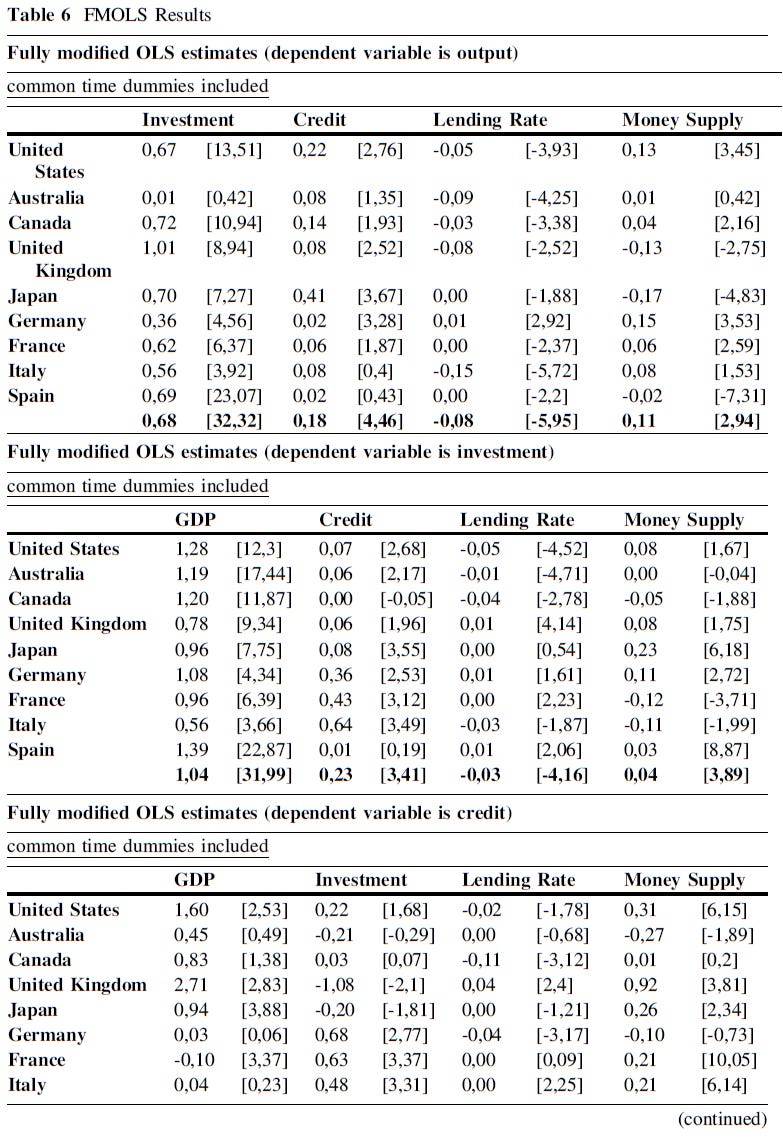
Results are given in Table 6. From panel estimates, when the dependent var is output (GDP); investment, credit, lending rate, and money supply have a coefficient of, respectively, 0.68, 0.18, -0.08, 0.11. When the dependent var is investment, GDP, credit, lending rate, money supply, have a coefficient of 1.04, 0.23, -0.03, 0.04. When the dependent var is credit; GDP, investment, lending rate, and money supply have a coefficient of 0.79, 0.15, -0.08, 0.21. When the dependent variable is money supply; GDP, investment, credit, and lending rate, have a coefficient of -0.58, 2.34, 1.07, -0.09. When the dependent var is lending rate; GDP, investment, credit, money supply, have a coefficient of -36.83, 34.99, 1.11, -3.19. Thus, money supply has an effect on interest rate and credit, and credit has an effect on investment, which in turn has an effect on GDP. This was the pattern predicted by the ABCT.

On a per country basis, when the dependent var is GDP, the impact of investment is null in Australia, the impact of credit is small or virtually non-existent in most countries. The same thing is true for lending rate and money supply. When the dependent var is investment, credit is too small for most countries, lending rate and money supply probably are not important variables either. When the dependent var is credit, the impact of GDP and investment vary greatly across countries, in effect size but also in sign, lending rate is near zero, and money supply has generally a positive coefficient but, again, varies greatly across countries. When the dependent var is money supply, the impact of GDP and investment vary in size and sign, and may not be very important, the impact of lending rate, although consistently negative, seems ambiguous, and the impact of credit seems to be the most consistent. When the dependent var is lending rate, GDP differs in size and signs, investment has a non-trivial impact, and credit and money supply have coefficients varying in size and signs.

Tsionas adopts Dufour et al. (2006) method of vector autoregressions for examining whether there are causal relationships between variables at various horizons. Causality is established when the significance level was below 5% or 10%.

In the US, interest rate is influenced by money supply, in short and medium term horizons (2-18). Credit in the medium term horizons is caused by money supply (2-3 and 8-26) and Credit in short term horizons is caused by interest rate (3-9). Credit causes investment from horizon 6 to 34. There is causality from investment to GDP (horizons 2-8 and 14). Credit also causes GDP over all horizons (2-34).

In Australia, interest rate causes money supply (2-12, 20-30), but money supply also causes interest rate (6-12, 18, 22-28). Interest rate causes credit in the short and medium term horizons (2-20). There is a bidirectional causal relationship between money supply and credit. There is causality from Credit to GDP (horizons 7-34).

In Canada, money supply is caused by the interest rate, and the interest rate causes credit over any horizon. Investment and GDP are both caused by interest rates, and GDP is caused by credit (horizons 9-34). There is no causal relationship between credit and investment. For each variable, the importance of interest rate is overwhelming.

In the UK, money supply is caused by credit (2-20, 30-34) and interest rate (2-16, 24-34). Credit is caused by GDP (4-20), investment (3-12), and interest rates (4-16, 22-34). Investment is caused by GDP, credit (2-20), and interest rate (4-14). GDP is caused by credit (4-34) and by investment (2-6).

In Germany, money supply is caused by interest rate (16-30). Interest rate is caused by investment (7-32) and credit (2-14, 24-34). The importance of money supply is overwhelming, as it causes credit, investment and GDP at nearly all horizons. Credit causes both investment and GDP. Investment also causes GDP at horizons 5-24 (not the reverse).

In Japan, money supply causes interest rate (2-14) and credit (8-34). Interest rate causes money supply, GDP, and credit (but only horizons 7-14, 22, 26). Credit causes investment (2-24) and GDP.

In France, money supply is caused by credit and also by interest rate (but for horizons 8-24). Investment (2-22) and money supply (2-10) cause credit. Interest rate (4-7, 9-26) and credit (2-26) cause investment. GDP is mainly caused by investment and credit, and perhaps by interest rate (10-26) and money supply (9-34) in the long term horizon.

In Italy, interest rate is caused by money supply (2-20), which is caused by credit and by investment (only in horizons 12-34). Credit is caused by interest rate (2-8) and money supply 2-9). Investment is caused by credit and by money supply (only at horizons 6-22 however). GDP is caused by credit (7-20, 26) and money supply (12-26).

In Spain, money supply is caused by credit (2-18), and credit is caused by interest rate and money supply. Investment is caused by money supply, and by interest rate, credit and GDP in the long term horizon. GDP is caused by investment in short term (2-9) and is caused by credit, interest rate and money supply in long term horizon.

To summarize, the causal chain theorized by the ABCT, that is, money supply causes lending interest rate, and both causing credit, which in turn causes both investment and GDP, appears generally tenable.

11. Austrian Business Cycle Theory: An Application to New Zealand’s Recent Boom and Bust (Roy Ruxton Davidson, 2013)

Davidson (2013) examines diverse data trends available for New Zealand, to see if the global financial crisis (GFC) of 2008 fits the theory. One prediction of the ABCT is the increase in money supply (due to artificial credit) leading to the business cycle. Chart 1 shows that M2 increases between 2000 and 2012, from a stock of $41,490m in January 2000 to $94,677m in September 2012, or 10% per year, while M3 increases even more, from from $96,182m in January 2000 to $245,502 in September 2012, or 13% per year. Chart 2 and 3 show the year on year growth rate of M2 and M3, respectively. M3 is less volatile, perhaps because it is a broader measure of money. But in both cases, the acceleration in money growth from 2003-2004 to 2007 is evident, after the decline in money growth occurred (from 2001 to 2003). Chart 4 depicts the trend in mortgage lending and other lending between 2000 and 2012. Both indices show a steady increase. Chart 5 shows that CPI is stable (around 2-3%) between 2000 and 2012. But the ABCT is a theory about production and price structures. It assumes nothing about the trend in “overall” prices. Chart 6 displays the trend in Official Cash Rate (OCR) and 90-day bank lending rate % for the period 1999-2012. Both are closely related and go up in 2000-2001 (4.5 to 6.5%), down in 2002 (5%), and begin again to increase steadily until a large drop in 2009-2010 (8-9% to 2.5%). This demonstrates that money supply has increased during the expansionary phase.

Another prediction is the decline in private savings. This is because the expansion is not caused by an increase in savings but merely by monetary injection. In Chart 7, we see there is a large decline in gross domestic savings (% of GDP) between 2000 and 2005, from 21% to 16%, and was only at 16% (or 18%) in 2009 (or 2010). Chart 8 shows the gross savings by sector (in % of GDP). The share of national and business (residual) remains stable between 1987 and 2009. The share of the general government increases over time (around 0% in early 1990s and around 7% in 2003-2007), but the share of households declines over time (+5% in 1988 and -5% in 2007-2009). Chart 9 shows the gross and net household savings as % of disposable income. Net and Gross display a large decline, respectively, +3% and +5% in 1992 to -13% and -10% in 2009. Chart 10 shows that the household consumption expenditure per person and per household increase over time. Given an index of 100, starting at 1992, the index peaks at around 140 in 2008. This is in line with the previous graphs showing a decline in savings.

Still another prediction is the relative increase in the value and price of higher-order goods, because the ABCT claimed that a boom will be accompanied by a lengthening in the structure of production. The more roundabout, capital-intensive industries will be the most affected. Chart 11 shows that the value of New Zealand’s private sector residential dwellings, while showing a steady increase between 1989 and 2007, has experienced a dramatic acceleration between 2002 and 2007. This value increased from approximately NZ$250 billion to over $600 billion, or 20% per year. Chart 12 shows the increasing trend in the NZX 50 index, between 2004 and 2007 (from 2.60K to 4.20K, or 15% per year). After 2008, the index shows a large drop (4.00K in 2008 to 2.80K in 2009). Chart 13 displays the Capital Goods Price Index (CGPI). There is a sharp increase between 2003 and 2005. A peak is evident in 2009, as well as the large drop in 2010. The Chart 14 depicts the PPI and it shows a steady increase between 2001 and 2008, a modest decline in 2009, before it starts increasing again. But a better measure would have been to look at the PPI/CPI ratio.

The consequence of money manipulation by authorities can be seen in Chart 15, where the rate of bankruptcies jumps between 2007 (around 300 per month) and 2009 (around 600 per month). In Chart 16, we can see the unemployment rate going up between 2008 and 2009, around 4% to 6-7%.

12. Austrian Business Cycle Theory: Did Iceland go through an Austrian Business Cycle? (Ragnar Haukur Ragnarsson, 2011)

Ragnarsson (2011) also examines the data available in Iceland (Statistics Iceland, Central Bank of Iceland). Figure 9 shows that gross savings in % of GDP declined between 2002 and 2006 (about 15% to 12%), increasing marginally in 2007, before the fantastic drop occurred in 2008 (with 1%). Figure 10 shows the steady increase in final consumption expenditure between 2002 and 2007 (from about 400,000 to about 550,000, in million Icelandic Krona, ISK). This is logical, given the drop in savings. Figure 11 shows the increase in total lending by the financial system, year end status, between 2000 and 2007, with an acceleration starting after 2003. Figure 12 shows the increase in three measures of money supply. The increase in M3 is larger than for M2, which is larger than M1, but each measure has been multiplied by more than twice, between 2004 and 2008. Figure 13 shows the (average) annualized rates for CPI and CPI less housing costs, from 2000 to 2010. There is clear evidence that consumer prices went up at the time the money supply was going up. CPI shows a steady increase between 2003 and 2006, but not the other measure perhaps because housing cost is left out in this index. That is consistent with the existence of a housing bubble. The large increase in CPI that was detectable in 2008-2009 is due to the onset of the recession. As explicited above, CPI trend is irrelevant for the ABCT. Figure 14 shows the trend in total debts of enterprises (excluding financial institutions and electricity and water supply). It increases between 2001 and 2008 but it accelerated after 2004. Figure 16 shows the increasing trend in residential housing price index (for capital area) between 2000 and 2008, with an acceleration after 2004. The housing boom is evident. Figure 17 shows that the price of the OMX Iceland All-Share PI went from 1.261,61 on the fourth of January 2001 to its highest on the eighteenth of July in 2007 when the price reached 8.174,28. The acceleration after 2004 is evident. Figure 18 shows the number of construction in residential housing. The number of dwellings has more than doubled between 2000 (about 1600 constructions) and 2005 (about 4400 constructions), remaining as high until 2007, before the dramatic drop occurring in 2008-2009. Figure 19 shows that the total turnover in construction increased from 2000 (about 80, in million ISK) to 2007 (about 260 in million ISK), before it declined in 2009 (about 130 in million ISK). Figure 20 shows that the profit in regular operation in construction has increased very much during the 2000s, until the dramatic losses in 2008. Figure 21 shows that the number of persons employed in construction as % of the total workforce between 2000 (around 7%) and 2008 (around 9-10%) is what can be expected given the housing boom.

13. An Empirical Illustration of the Austrian Business Cycle Theory: The case of the United States, 1988-2010 (Neira, M. A. A., Bagus, P., & Ania, A. R., 2013)

Neira et al. (2013) studied the US business cycles between 1988 and 2010. All series come from the FRED of Bank of St Louis, except the data on construction that was retrieved from the Board of Governors of the Federal Reserve System. The variables, except interest rates, are measured in deviations from their trend (calculated using the Hodrick-Prescott filter) to ensure stationarity. Table A1 shows that all variables considered are stationary at 5% level. Money supply is MZM. The cyclical deviations of the MZM are obtained from the expression ΔMZM_t = ln(MZM_t/trendMZM_t). ln stands for natural logarithm (or log). The interest rate gap is the difference between short- (3-months) and long-term (10-years) maturities. The difference is calculated as DIF_t = ln[(1+i_10a)_t/(1+i_3m)_t].

It is expected that the variations in the slope of the yield curve (represented by DIF_t) will have an effect on the production structure. Seven ratios are constructed. The cyclical fluctuation in production structure are estimated from the following ratios : ΔK_1t (capital goods to consumer goods), ΔK_2t (durable consumption goods to consumption goods), ΔK_3t (construction to consumption goods), ΔK_4t (durable materials to consumption goods), ΔK_5t (durable materials to non-durable materials), ΔK_6t (durable manufacturing to non-durable manufacturing), and ΔK_7t (durable consumer goods to non-durable consumer goods). An Industrial Production Index (IPI) has also been constructed and is calculated given the deviation from its trend (ΔIPI_t).

Granger causality reveals that ΔMZM_t causes DIF_t. They also report a correlation higher than 0.80 between ΔMZM_t and DIF_t. The next chain of the causality involves Granger causing the interest rate gap on each of the ΔK ratios. Regarding ΔK_1t, they found such causality, with no evidence of feedback effect (i.e., reverse causality). But there was no causality from the interest rate gap to ΔK_2t. In fact, ΔK_2t Granger causes interest rate gap for lags 1-4. As for the explanation of no causality, they suspect that the production of durable consumer goods does not include the activity related to the construction sector, except for computers, audio and video, appliances, and vehicles. In fact, starting from 2001, the credit expansion channeled mainly into the mortgage market but to the expense of other sectors for the production of consumer goods in general. DIF_t causes ΔK_3t and ΔK_4t and ΔK_5t and ΔK_6t without reverse causality. This can be seen in Table A2. The number of observations ranges between 82 and 91, depending on the number of lags specified.

Also, we can see that DIF_t causes ΔIPI_t at lags 2-7 but that ΔIPI_t causes DIF_t at lags 2-9. To make things even worse, the F stats for the causation ΔIPI_t->DIF_t is even larger than the F stats for the causation DIF_t->ΔIPI_t. They argue that was symptomatic of the marked counter-cyclical monetary policy adopted by the Federal Reserve during the period of 1988-2010.

Figure A3 shows the correlations between interest rate gaps at time t and different lags (t-i) of the cyclical behavior of MZM. The first positive correlations confirm that monetary expansion generates a liquidity effect until the 4th or 5th quarter. Starting from quarters 8-9, the coefficient becomes negative, and remains so until quarter 20. This illustrates the idea that the slope of the yield curve tends to reverse (elevating at the beginning and then flattening at the end), as resource constraints (related to the boom) begin to emerge. But it is also possible that the intervention of the Fed (through monetary contraction) has accentuated this reversal.

Graph 4 shows that the trend in the ratios of K1, K2, K3, K4 and IPI is consistent with the prediction, except that K2 fluctuates too modestly (not surprising given the above discussion). Graph 5 shows the trend in the ratios K5 (meaningful), K6 (modest), K7 (non-existent). Both graphs depict the effect of lagged interest rate gap on the structure of the sectors of production. That the ratios show an increasing (decreasing) trend during the boom (bust) is an illustration of how the resources are (mis)allocated toward more capital-intensive industries.

These graphs are derived from an analysis involving a model of polynomial distributed lag on the variables of production, which results are given in Table A4 showing the relationship between the K ratios illustrating the cyclical behavior of intertemporal capital structure (ΔK_Jt) and the slope of the yield curve after making appropriate adjustments to avoid problems of residual autocorrelations. As can be seen, K2 and K7 ratios do not have large cyclical behaviors. Unlike with Granger test, we see there is a pattern in IPI that is predictable by the ABCT. The fact that IPI presents mixed results is just in line with most research.

14. An Overinvestment Cycle in Central and Eastern Europe? (Andreas Hoffman, 2010)

Hoffman (2010) examines the effect of easy EMU liquidity on the Central and Eastern European (CEE) economies. The data come from the IFS of IMF. He attempts to Granger cause the European Monetary Union (EMU) interest rate gaps (defined as long minus short-term rates) on each of the CEE countries, namely, Bulgaria (BU), Czech Republic (CZ), Estonia (EE), Hungary (HU), Lithuania (LT), Latvia (LV), Poland (PL), Slovenia (Sl), Slovakia (SK), Romania (RO). Only Estonia and Slovenia show no evidence of causation in either direction. In other countries, the causation is generally from EMU interest rate gap to (one of the) CEE country’s interest rate gap. Easy liquidity conditions from EMU may transfer to CEE economies.

Figure 4 shows that the credit to the private sector in Poland, Estonia and Romania has amplified between 1995/1997 and 2008. Figure 5 shows the trends in asset prices in Poland, Estonia and Romania, and they share similarities. An increase since 1998 that has greatly accelerated started from 2003-2004 but followed by a considerable drop after 2007. Figure 6 shows the trends in production of capital and consumer goods for Estonia and Romania. During the 2000s, in both countries, the production of capital goods increased relative to the production of consumer goods, while in recession, the drop in production was much more pronounced in capital goods. Figure 7 shows that the ratio of money supply to GDP has increased from 2003 to 2007 but declined in 2008, in Poland, Estonia and Romania. Figure 8 shows that after 2005, the composite indicator of credit boom signals a credit boom. This composite is an average index for the CEE of investment/GDP, money/GDP ratios and asset price development from the Hodrick-Prescott (HP) trend. It was based on Eichengreen and Mitchener (2003) measures of overinvestment boom. Their reason for using such an index is because “there is a broad consensus that credit booms are hard to spot before the event of the crisis, because high growth rates of output and credit to the private sector may also be justified by financial deepening (Beck et al., 2000), new technology, institutional change (as explained by Hayek and Schumpeter) or—as in the case of CEE—the accession to the EU and the expectation of euro adoption.” (p. 726).

3. References.

1. Bjerkenes, H., Kiil, H., & Anker-Nilssen, P. (2010). Austrian Economics: Application on Norwegian Business Cycles. Dissertation.

2. Davidson, R. R., (2013). Austrian Business Cycle Theory: An Application to New Zealand’s Recent Boom and Bust. Dissertation.

3. Hoffmann, A. (2010). An Overinvestment Cycle in Central and Eastern Europe?. Metroeconomica, 61(4), 711-734.

4. Lester, R. B., & Wolff, J. S. (2013). The Empirical Relevance of the Mises-Hayek Theory of the Trade Cycle. The Review of Austrian Economics, 26(4), 433-461.

5. Luther, W. J., & Cohen, M. (2014). An Empirical Analysis of the Austrian Business Cycle Theory. Atlantic Economic Journal, 42(2), 153-169.

6. Luther, W. J., & Cohen, M. (2014). On the Empirical Relevance of the Mises-Hayek Theory of the Trade Cycle.

7. Montgomery, M. R. (2006). Austrian Persistence? Capital-Based Business Cycle Theory and the Dynamics of Investment Spending. The Review of Austrian Economics, 19(1), 17-45.

8. Murphy, R. P., Barnett II, W., & Block, W. E. (2010). Testing Austrian Business Cycle Theory? A Rejoinder to Andrew Young. Journal of Business and Economic Perspectives, 36(2), 14.

9. Murphy, R. P., Barnett, W., & Block, W. E. (2012). Testing Austrian Business Cycle Theory? A Second Rejoinder to Andrew Young. Romanian Economic Business Review, 7(3), 7-20.

10. Neira, M. A. A., Bagus, P., & Ania, A. R. (2013). An Empirical Illustration of the Austrian Business Cycle Theory: The case of the United States, 1988-2010. Investigación Económica, 72(285).

11. Ragnarsson, R. H. (2012). Austrian Business Cycle Theory: Did Iceland go through an Austrian Business Cycle?.

12. Russell, L. A., & Langemeier, M. R. (2014). Austrian Business Cycle Theory: Evidence from Kansas Agriculture. Paper presented at the Texas Tech University Free Market Institute Friday.

13. Schnabl, G., & Hoffmann, A. (2008). Monetary Policy, Vagabonding Liquidity and Bursting Bubbles in New and Emerging Markets: An Overinvestment View. The World Economy, 31(9), 1226-1252.

14. Tsionas, E. G. (2014). International Empirical Evidence on the ABC’s of Recessions. In The Euro and International Financial Stability (pp. 285-308). Springer International Publishing.

15. Whittle, R. (2012, submitted for 2014/2015?). Austrian Business Cycles: From Theory to Empirics.

16. Young, A. T. (2005). Reallocating Labor to Initiate Changes in Capital Structures: Hayek Revisited. Economics Letters, 89(3), 275-282.

17. Young, A. T. (2011). Illustrating the Importance of Austrian Business Cycle Theory: A Reply to Murphy, Barnett, and Block; A Call for Quantitative Study. The Review of Austrian Economics, 24(1), 19-28.

18. Young, A. T. (2012). The Time Structure of Production in the US, 2002–2009. The Review of Austrian Economics, 25(2), 77-92.