Income mobility according to the Great Gatsby curve : The fantasy of the american dream, statistical artifacts, and the irrelevance of public intervention.

Jun 26, 2014

Among the economists, it is commonly held that US people do not experience high income mobility. This is true. But the question of whether US people have lower income or social mobility compared to european countries has no definitive answer. The gender gap has never been considered. Between-countries analyses (which could be biased by confoundings in between-country differences in cultural and political conditions) have not been supplemented by within-countries inequality-mobility relationship over time. The former is inconsistent with the latter. Measurement issues and statistical artifacts need to be better understood. Regardless, what is known as the Great Gatsby curve is that the higher the social inequalities and the lower the income mobility. The evidence for it has been generally well supported (Blanden, 2013).

But a more relevant information is to look at the low(est) income categories. If this specific portion of the income distribution has similar upward mobility between the US and european countries, then the main assumption behind the Gatsby curve should be seriously revised.

One instance of authority, the OECD (2008, p. 206), has displayed the data taken from Jantti et al. (2006) showing that, among the lowest income category fathers, the sons have much larger probability to remain in the lowest income category in the United States than in other countries, especially the Scandinavian regions in Europe. Reading it, one thing strikes me. Why is there no mention about income elasticities for the daughters ? They have large and strong data sets but only for men, not women ? That does not make sense. I was curious to examine the sources. Happily, my first impression was right. The likely reason why OECD did not bother to mention the data for women is because it refutes their preferred theory. I never trusted OECD, and this detail again will not make me change my mind. In fact, quite a lot of researchers citing the Jantti’s study refer only to the male data, which is not surprising considering that science related to politics is (almost) always moved by ideology. But the fact the OECD does the same is even more unforgivable.

CONTENT [Jump links below]

1. Introduction
2. Empirical Studies
3. Measurement Issues
4. Genoeconomics

1. Introduction to some statistical things.

Difficulty with regard to cross-national comparison must be dealt with. And problems such as short time span, (too) young age of the offspring, unreliable data, differences in years studied etc., must be avoided. The references listed in section 2 seem to have more or less avoided the pitfalls.

To be sure, we must precise that elasticities and correlations are close but not exact same concepts. Corak (2004, pp. 10-11), Blanden (2013) Black & Devereux (2010, pp. 5-6) inform us that the intergenerational elasticity (IGE) must be understood by the simple regression equation : log(Y1)=α+βlog(Y0)+ε, where log(Y1) the log income of the offspring (1), α is the constant or the average income of the children’s generation, and the deviation from this average is determined both by βlog(Y0) the regression coefficient of log income of the parent (0), and by the error (ε) term. An alternative elasticity is the intergenerational correlation (p) and is formulated as p=(σ0/σ1)*β, where σ is the standard deviation (SD) of log earnings of either offspring or parent. Mobility can be thought as measured by 1-p. Elasticity is said to be unbiased by measurement error in y1 (Baron & Kenny, 1986, p. 1175) but elasticity β can still be biased by measurement errors in y0 thus there was a need to use a so-called permanent income variable (i.e., averaged over many years). The assumption of equal variance is crucial because they differ between population or generation, as it would appear if the magnitude of inequality varies over time, the slope coefficient β will estimate β=p*σy1/σy0 rather than the correlation p itself (e.g., lower SD in parents results in β stronger than p), as noted by Solon (1992). That is why, the correlation p is not supposed to be affected by changes in SD over time. Black & Devereux (2010) recommend to report both measures. Conceptually, elasticity and correlation differ as Jäntti (2006) describes:

The elasticity is, however, a measure of average persistence of income rather than of mobility. In other words, the regression coefficient on father’s log (permanent) earnings tells us how closely related, on average, an offspring’s economic status is to that of his or her parent. It is quite possible for two countries to have highly similar average peristence, but for one to have substantially more mobility around that average persistence. The elasticity can thus be the same, but arguably the country with a greater residual variation – that is, variability around the average persistence – is the one with greater mobility. Moreover, two countries with the same regression slope may have quite different, and varying, conditional variances around that slope. For instance, a country with a “bulge” in the variance at low levels of fathers’ earnings, that is, a pear-shaped bivariate distribution, will exhibit relatively more mobility at the low end of the distribution than will a country with a constant conditional variance.

The difference is relevant. As Black & Devereux (2010) noted with regard to Jantti’s study, “The differences between the elasticities and correlations reflect differences in the variances of earnings in the fathers’ and sons’ generations. For example, the elasticity is higher than the correlation for the US due to the increase in earnings inequality in recent decades.” (p. 15). In other words, standard deviation matters. Perhaps the correlation (p) is more appropriate, after all.

Generally, one serious shortcoming of most studies is the use of relative rather than absolute mobility. Chetty et al. (2014a) commented on the utility of absolute mobility : “Measuring absolute mobility is valuable because increases in relative mobility have ambiguous normative implications, as they may be driven by worse outcomes for the rich rather than better outcomes for the poor”. And Corak et al. (2014) tell us that moving the same distance in terms of percentile rankings does not necessarily imply equal changes in earnings. Chetty et al. (2014a) illustrate as follows:

For example, if one defines mobility based on relative positions in the income distribution – e.g., a child’s prospects of rising from the bottom to the top quintile – then intergenerational mobility has remained unchanged in recent decades. If instead one defines mobility based on the probability that a child from a low-income family (e.g., the bottom 20%) reaches a fixed upper income threshold (e.g., $100,000), then mobility has increased because of the increase in inequality. However, the increase in inequality has also magnified the difference in expected incomes between children born to low (e.g., bottom-quintile) vs. high (top-quintile) income families. In this sense, mobility has fallen because a child’s income depends more heavily on her parents’ position in the income distribution today than in the past.

These authors also recommend the use of rank-rank (parent-child) specification instead of log-log specification, because log omits observations with zero income. If children of low income parents are much more likely to have zero income, dropping these observations over-estimates mobility. Also, the relationship of (log) parent-child income is highly non-linear, with much lower local IGEs below the 10th and above the 90th percentile. And IGE estimates are sensitive to differences in local income distributions.

A concept worth considering is the distinction between short- and long-term inequality. In fact, a short-term (transitory) inequality can increase while long-term (permanent) inequality remains stable if mobility increases (Kopczuk et al., 2010, pp. 95-99). This will result in a stable rank-based mobility along with an increase in variance of transitory earnings.

2. Empirical studies.

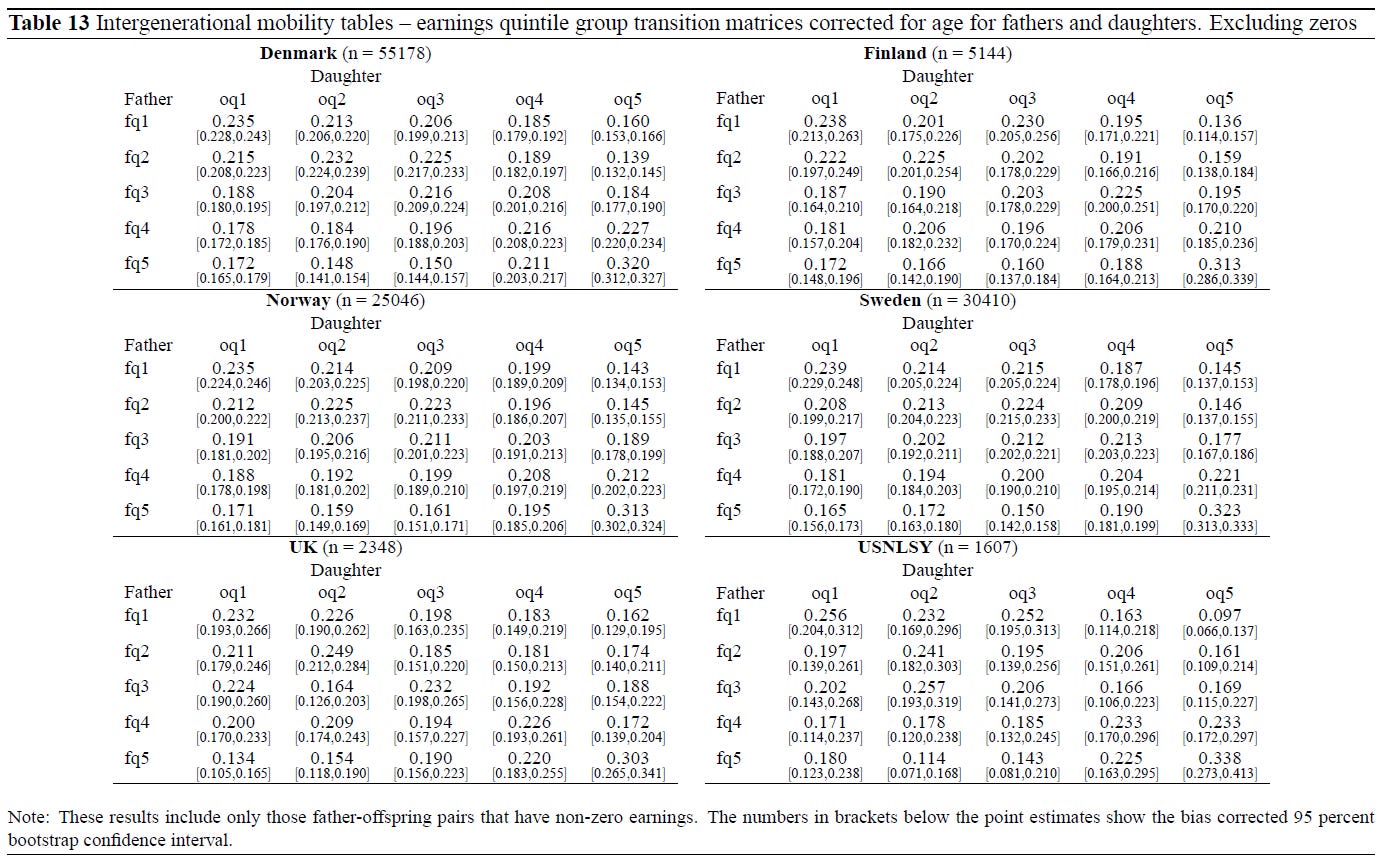
Jäntti et al. (2006) compared income mobility across countries, not by correlating parental income with children earnings (parametric test) but by using mobility transition matrices (a non-parametric test which is sometimes called transition probabilities) to compute the mobility rates (see Hirvonen, 2008, p. 803, for a description). Lower mobility is supposed to be reflected by higher correlations because it means that the children earnings is more dependent on that of their parents. Compared to UK and US, they found lower correlation among Nordic countries for men, but not especially for women. They use the NCDS for UK and NLSY for US, each surveys were based on the respondents’ self-reported earnings (for NCDS, parental income for the year when the offspring was 16 years-old, offspring income when they were 33 and 41; for NLSY, year 1978 for parental income, 1995 and 2001 for offspring wage and salary income). Norway, Finland, Denmark, Sweden, have administrative register data. Thus, the data for scandinavian countries is undoubtedly stronger. For Norway, father’s earnings was from 1974, offspring earning are measured in 1992 and 1999, For Sweden, father’s earnings were from 1975, and offspring from 1996 and 1999. For Denmark, father’s earnings were from 1980, and offspring from 1998 and 2000. For Finland, father’s earnings were from 1975, offspring from 1993 and 2000.

The fathers were in their 45-50 yrs-old, their earnings data measured in the mid 1970s, the sons and daughters are born around 1960 and their earnings measured in the mid 1990s, with the youngest and oldest offspring having 30 and 42 years, respectively. These were similar in order to get comparable cross-national results.

American Exceptionalism in a New Light - A Comparison of Intergenerational Earnings Mobility in the Nordic Countries, the United Kingdom and the United States (Jantti 2006) Table 13

In these tables, the 5 diagonals (fq1-oq1, fq2-oq2, fq3-oq3, fq4-oq4, fq5-oq5) in each of the matrices in tables 12-15 also show us that in every countries the probability for men of staying in the quintile is greater at the extremities, and the immobility is stronger at the highest than at the lowest quintile. For women however, in every country, the probability of staying in the quintile is higher only at the 5th quintile. In general, women seem to have a somewhat lower elasticity.

The table 13 shows why most researchers prefer not to mention the data for women. There is no clear US/UK and Nordic difference for the women. The author, Jantti, speaks in bad faith as it is argued that women data is less precise, and thus, less reliable. Based on what ? Less precise means that the standard error, p-value and confidence intervals (CIs), which are all related, are larger for women data. A lower precision happens when the sample size is lower. The CIs were shown above, and we can see they are not wider for women. There is no indication these numbers are less reliable due to sampling errors. The sample sizes (n) were almost equal for men and women, after all.

The robustness check using two-year measures, instead of single-year measures, does not affect their result so much, as illustrated in Table 7, above. Interestingly, the Europe-US disparity is somewhat less. This is quite unexpected because measurement error due to self-report variables in the US (and UK) data is expected to lower the correlations. Thus, more reliable data should have increased the Scandinavian-US countries disparity somewhat. But it is possible that 2-years averaging is not sensitive enough or that the income measure from Nordic countries was almost free of measurement error. Furthermore, the data for Nordic countries is less inclusive than for UK and US. Income may plausibly reflect only a portion of economic background.

Thus, another concern for robustness was that parental earnings data in Nordic countries include only labour earnings while family income from all sources are available for US and UK. To deal (somewhat) with this issue, they have summed the earnings of both parents in Finland, Norway, and Sweden, and make new comparisons. Thus, when we compare table 2 and 9, for men, in Finland, the correlations have increased whereas for the two other Nordic countries, they have decreased. For women, the correlations increase in Finland but decreased in Sweden. Overall, there is no meaningful change. Generally, the method of averaging reduces measurement error, and leads to an increased correlation. But since the data in Nordic countries has no measurement error (only year-to-year variations) this result is not necessarily surprising.

When they use weekly earnings instead of annual earnings (by dividing annual earnings by number of weeks worked during the last year), for the US, there is a decrease in the correlation (Table 8) for the cells of lowest income father to offspring lowest quintile, from 0.422 to 0.362 for men, from 0.256 to 0.227 for women. The cells highest income father to offspring lowest quintile (0.095 to 0.067 for men, 0.180 to 0.137 for women) and highest income father to offspring highest quintile also show a decrease in correlation (0.360 to 0.318 for men, 0.338 to 0.309 for women). There is strong evidence that, in the US at least, the use of weekly (instead of annual) earnings produces lower correlations. If the US disadvantage in terms of mobility would show up in working time and in unemployment, the authors suggest that the US-UK differences could have been exaggerated because the UK data has only weekly earnings. This further implies that if the Nordic countries had weekly earnings, the UK-Nordic difference may have been stronger than what actually is. But, some conflicting numbers prevail, as Hussain and others (2009) found an earning elasticity in Denmark (administrative data) for father-son of about 0.224 when using hourly wages and 0.123 when using annual wages. On the other hand, Solon (1992) confirmed a lower elasticity found in the US (PSID) when using hourly wages as opposed to annual earnings.

A last sensitivity check reveals that the US income elasticity decreases non-trivially when ethnic minorities such as blacks and hispanics are removed from the analysis. This is an important detail since they represent a large portion of that country. Regarding the probability that the son of the lowest income father will remain in this category, it goes down, from 0.422 to 0.381. Clearly, this makes a difference. Unfortunately, they have not displayed the numbers for women. I am wondering why.

In their conclusion, they argue that the belief in american dream is held among middle classes, which represent a substantial fraction of the voters, while the lower classes believe they have low chances of experiencing upward mobility. Interestingly, the US middle class is as likely to be mobile as in the UK or Scandinavian countries.

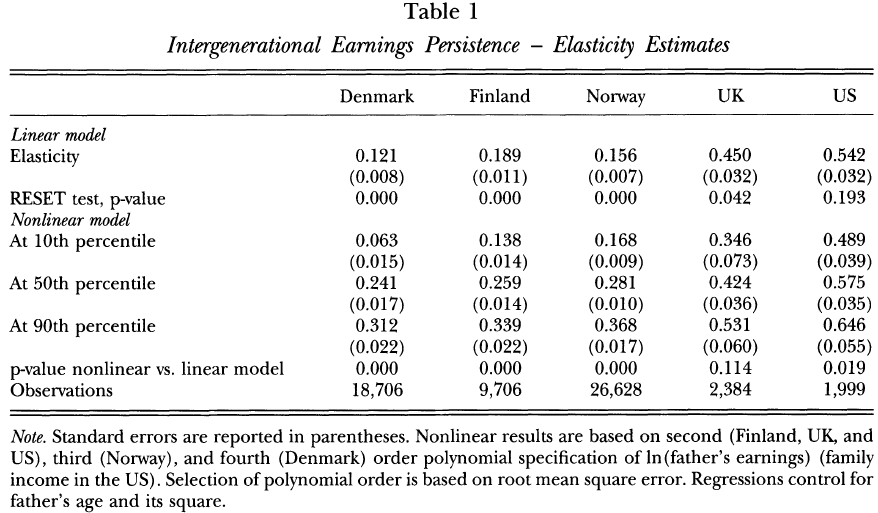
Another study was from Bratsberg et al. (2007) who find lower elasticities between fathers’ and sons’ permanent (log) earnings. In Nordic countries however, the correlation is not linear but convex. One obvious problem is that they have not conducted the analysis for women. However, it provides an alternative to the Jantti’s study in that a different statistical method is used. The data for UK and US are from (respectively) NCDS and NLSY79 surveys. Norway, Denmark, and Finland have pension and tax registers, again. Only the NLSY79 has family income data (for parents) instead of father’s income.

Nonlinearities in Intergenerational Earnings Mobility - Consequences for Cross-Country Comparisons (Bratsberg 2007) Table 1

In their original model, Table 1, we see for each countries that earnings persistence (or elasticities) of the sons increases with the percentile of the father’s earnings. In Denmark, the elasticities in the non-linear model, at 10th, 50th and 90th percentile, were 0.063, 0.241 and 0.312. The respective numbers were 0.138, 0.259 and 0.339 for Finland, 0.168, 0.281 and 0.368 for Norway, 0.346, 0.424 and 0.531 for UK, 0.489, 0.575 and 0.646 for US. In the linear model, the elasticities are 0.121, 0.189, 0.156, 0.450, 0.542, for the respective countries.

They attempt to test the robustness of the non-linearity pattern. The first problem is that of measurement error, particularly for both the extremities. Their longitudinal panels allow them to use income averaged on two observation years versus 10 years for Norway. This provides a test against lifecycle bias. It was believed that more years will average out errors and thus leads to an increased correlation. But comparing tables 1 and 3, income elasticity increases slightly in nonlinear model and declines slightly in linear model. It was probably due to sampling bias, due to the inclusion for the longitudinal averaging income of fathers reporting of zero earnings in single years. Thus, their inclusion in the sample exacerbates the specification error of the linear model. When they restrict the sample to fathers with non-zero earnings in every years, there had been evidence for attenuation bias (i.e., bias toward zero) in single-year based estimates, which means that multiple-year averaging improves the correlation.

A further question is the inclusiveness of the income data. Using either the father’s income or family income produces little difference. Since family income (mother+father) is more inclusive, it must result in reduced measurement error but also in different estimations if family and father income have different properties. The impact seems small, with estimations becoming lower in Norway and UK but higher in Finland and Denmark, in both specification models. There is one ambiguity in Denmark where the elasticity at 10th percentile jumped from 0.063 to 0.153 when using family income. So, it is not clear what kind of effect the use of family income should have.

Another threat is the selection bias regarding fathers. In Denmark and Norway, fathers and sons are matched through birth records. Thus, in cases where sons are separated from their biological father, the use of father’s earnings may not accurately reflect the son’s economic circumstance during childhood and adolescence. To deal with this, they restrict the danish and norwegian samples to families where the mothers and fathers live together because it raises the probability that the son also lives with the father. The results did not differ meaningfully.

The next threat is selection bias regarding the sons, if the probability of reporting zero earnings is inversely correlated with parental income. The very fact that Nordic countries have generous welfare systems can make labour market withdrawal (i.e., unemployment) more attractive. If so, the elasticities at low (parental) income levels will be biased downwardly in Nordic countries, and thus accounting for the spurious non-linearity. Unexpectedly, the negative correlation between parental income and the son’s probability of reporting zero earning is stronger in UK and US, not in Nordic countries. As if to say that moral hazard behaviors can be predicted in UK and US based on parental income, but not in Scandinavian countries.

Another problem related with measurement error is under-report. Some fathers in the 1970s who report having low income may have in fact high income levels. If true, they would accumulate greater economic wealth later in life than is typically found in low income levels. Figure 7 samples the individuals still alive in 1994. The pattern of non-linearity still holds. They proceed to the last checking, and they find that low income fathers in nordic countries are recorded with much lower earnings than their counterparts in UK and US. They wondered if these numbers have not been under-estimated because if true it would bias the correlation toward a non-linear pattern. So, they exclude the earnings below $3000. The income elasticity increases modestly but the pattern of nonlinearity is still present.

Couch & Lillard (2004, Tables 8.4 & 8.5) compare Germany (GSOEP) and the USA (NLS Older-Cohort 1966-91). The german and us samples for sons’ age 18+ amount to 657 and 1694 sons, and for sons’ age 25+ amount to 549 and 1398. But unlike Jantti (2006) and Bratsberg (2007) who also use the NLS data, they report an average (log) earnings elasticities (transition matrices computed based on regression estimates) for father-son (aged 25+) to be 0.227 in Germany and to be only 0.215 in the USA. This is also unexpected given that Germany is generally viewed as more mobile than the US (Blanden, 2013) in terms of income. In both countries, the lowest quintile has more mobility than the highest quintile. And the non-linearity effect is stronger for the group of sons aged 25+. Curiously, the SD of earnings for the fathers was much stronger than the SD of the sons in the NLS but not GSOEP data. Regardless, if the equality in income mobility is true, despite strong differences in public policies, it tells us that the policies matter, not only quantitatively, but also qualitatively. If not replicated (Blanden, 2013), this poses the question as to why the estimates are so wide.

Another way to evaluate elasticities is by way of sibling correlations. Schnitzlein (2014) reports brother (sister) correlations of 0.202 (0.187) for Denmark (IDA), of 0.432 (0.391) for Germany (SOEP), of 0.450 (0.285) for United States (PSID). Remarkably, the use of another method once again reveals a huge gender difference in USA. The brother and sister correlations for earnings (0.479 and 0.347), family income (0.529 and 0.391), wages (0.457 and 0.437), education (0.656 and 0.551) was also estimated for Germany. The sample for brothers and sisters is larger in Denmark (73,554 and 68,062) than in Germany (1,014 and 704) or in the US (1,435 and 1,538). The mean age was, respectively, ~39-40, ~36-38, ~39-40. The years of measured earnings were in the early 2000s. Only the Denmark has administrative data, the others are just surveys with self-reported earnings.

The consistency of the lower sibling correlation for sisters was also reported elsewhere. Björklund et al. (2002) report sibling (brother) correlations of 0.230, 0.264, 0.138, 0.250, 0.429, for Denmark, Finland, Norway, Sweden, and USA. Applying different criteria, Björklund et al. (2004b) other study reports higher brother than sister correlations for Finland (0.242 vs 0.114), Norway (0.142 vs 0.122), Sweden (0.203 vs 0.150). For, Finland, there was no information on whether the children are biological siblings, thus they are just referred as social siblings. Norway also has a sample of social siblings and these correlations were 0.189 and 0.146 for brothers and sisters. Long-run earnings was the variable used, and consisted in averaging earnings of many years. All countries have administrative data, except for the US survey data, which is subject to some measurement errors. In all of these sibling studies, the year of birth and of measured earnings were similar across countries, in order to facilitate comparability. The larger gender gap in Finland is surely not explainable in terms of sampling error even though the N is lower than in Norway and Sweden (~19,000 vs ~583,000 vs ~220,000 and ~210,000). Thus, the general picture is that the gender gap is small, and is only large in the US, and Finland to a lesser extent.

Björklund & Jäntti (2000) present the intergenerational correlations of occupational status between fathers and sons, using the same status scale, for matter of comparability. And the pattern is all the more interesting. Compared with several european countries, the America seems to have the lowest father-son correlations. In other words, the US appears more mobile in terms of education. One problem is the modest sample size of most european countries, which seriously limits comparability. However, smaller samples may be accompanied with less accurate estimates and some possible range restriction. Both of them will act in biasing downwardly the correlations. If true, it suggests the US-european difference will magnify when corrected for statistical artifacts. Another factor biasing upwardly the US estimates is the apparently larger racial diversity in the US, which may account for some of the immobility in the US, as black people, for example, have lower upward income mobility than whites (EMP, 2007; Bhattacharya & Mazumder, 2011).

Intergenerational Mobility of Socioeconomic Status in Comparative Perspective (Bjorklund, Jantti, 2000) Table 6

The SES measure in use was the same for purpose of valid cross-national comparisons. If, for example, a variable is differently measured, have different number of values or categories, or questions, this may cause the respondents to respond differently. Thus, the variables do not measure exactly the same construct or factor.

Blanden (2013) confirms the striking difference across (developed) countries. When looking at social class mobility, Germany is among the less mobile, US the most, but this somewhat reverses when looking at income. It is noteworthy to remember that the Scandinavian countries perform relatively well whatever the measures we use.

Given the obvious correlation between status and income, it seems odd to see that the US has an advantage in terms of education mobility but not in incomes. However, the relationship between the two is not perfect, so this discrepancy may not be surprising. Income can still vary if people with equal education or occupation level receive different earnings.

There is, however, another possibility. Raaum et al. (2007, pp. 28-29, Tables 3-B & A-2) use the same data as in Bratsberg (2007) and look at the intergenerational correlation parents’ earnings against the offsprings’ years of schooling. They were similar in a linear regression model (Table 3-B), but when non-linearity has been modeled, the general pattern is that elasticity in US is stronger than in other countries at the 10th percentile of parental earnings, whereas it is lower at the 90th percentile. There is one ambiguity they don’t even bother to mention. The elasticity for married men in US is lower than for married men in UK at the 10th percentile of parental earnings and it does not seem to be much stronger than in Nordic countries either. Thus, when the authors said that non-linearity applies to all countries except US, they are just speaking lies. Furthermore, their variable of interest has limitations concerning its meaning across nations.

Marital Sorting, Household Labor Supply, and Intergenerational Earnings Mobility across Countries (Table A-2)

Another study sheds some doubts about the findings reported by Jäntti (2006). It comes from Corak et al. (2014) who applied the method of transition probabilities, using percentiles instead of quintiles, as suggested by Bhattacharya & Mazumder (2011). They compare Canada, Sweden, and US. All countries have administrative tax data; Statistics Canada, Statistic Sweden, and for the US, the Survey of Income and Program Participation (SIPP) matched to administrative earnings records maintained by the Social Security Administration (SSA). The authors seem to prefer, and rightly, the use of IGC instead of IGE since the former is not affected by differences in SD over time. They analyze father’s income and son’s income relationship (not daughters). The IGCs for Canada, Sweden, US, are, 0.23, 0.21, 0.26. The difference is small. An alternative measure is the intergenerational correlation in percentile rankings in earnings, which is simply the father-son Spearman rank correlation (a non-parametric test that deals with rank order and is thus not affected by SDs of the variables). The rank correlation is 0.24, 0.30, 0.30, for the respective countries. However, they noted that “the U.S. sample is relatively small compared to the other samples and the Swedish sample contains earnings covering a longer period of time. If we re-estimate the aggregate numbers for Sweden after first recasting the Swedish data so that it looks more like the U.S. data, then we actually see larger differences between the two countries along all three measures”. The US and Swedish IGEs are 0.40 and 0.24 whereas the IGCs are 0.26 and 0.16. These numbers are generated from a linear model. When non-linearity is modeled, they become more interesting.

A Comparison of Upward and Downward Intergenerational Mobility in Canada, Sweden and the United States (Corak 2014) Figure 10

Firstly, given Table 2, the transition probability out of the bottom quintile (i.e., 1 to 20th percentile) is 69% in Canada and 68% in both Sweden and the United States. Another look is given by Figure 3 (above) which plots the pattern of upward directional rank mobility (UP), specifically, the probability that the son exceeds the father by at least 20 percentiles (UP-20) for each countries. The difference is small again. In the Figure 4, which plots the differences in average percentile gains, we see that the US sons gain 2 or 3 percentiles less than the sons in Canada, and only 1 percentile less than the sons living in Sweden. But they argue the US data suffer downward bias by about 2-4%. The transition probability of moving out of the bottom 5 percentiles should have been 92% and not 88%, while the probability of rising out of the bottom quintile should have been 70% and not 68%. When they look at the downward mobility, at the top of the distribution (96th+), Canada, Sweden and US have 55%, 46% and 44% of sons who fall 20 percentiles below their fathers. But relative mobility, as the authors maintained, tells us nothing about the absolute mobility. Moving the same distance in terms of percentile rankings does not necessarily imply equal changes in earnings. This has been certainly under-studied. Figure 10 helps to understand its relevance, as we see that the sons whose fathers were in the bottom 5 percentiles of the earnings distribution have gained (compared to their fathers) about $17,000 in the United States, $19,000 in Sweden, and $24,000 in Canada, despite the countries having similar upward (relative) mobility. They speculate the reason is due to the larger inequality prevailing in USA. At the same time, Figure 11 shows that the sons in USA lose much more money in downward mobility at the very top of the distribution.

As we have seen, there is a difference between choosing income or education, or occupation, and even among the type of income used. And possibly a difference between the statistical methods applied, or the samples analyzed.

But analyses between countries are ineffective. A more informative study is a correlational trend over time. Results for these inequality-mobility correlations over time within countries (mostly within the United States) reveal that the tenets of the Great Gatsby Curve are falsified.

Saez & Veall (2005, Figure 7) examine the income (administrative) data in Canada from 1982 to 2000. The increase in income share to the top 0.1% has been accompanied by a stability of staying in the top 0.1%. This proves no point for either side. They argue that income taxes assessed at the individual level and those based on family income may not be directly comparable. But as Figure 6 shows similar trend for both estimations, this factor can’t explain the increasing trend.

Kopczuk et al. (2010) use the Social Security Data to examine the trend in earnings inequality (Gini and earnings ratios 50th/20th and 80th/50th) and mobility in the US between 1937 to 2004. No relationship emerges. The increase in the top 1% earnings share between the 1980s and 2000s has been accompanied by a stability in percentage of staying in this top 1%.

Relying on PSID and NLSY79 survey data for the US, Bloome (2013) demonstrates there is no relationship between family income inequality and intergenerational mobility across states and over time. Figures 1 & 2 show the trend in inequality and mobility and the two variables do not move together over time. But a state-year fixed effects design is a more robust test, to the extent that it controls for between-state differences (e.g., policies, racial composition) over time. Bloome further states that a change in inequality may cause a change in politics that affects mobility (e.g., toward less, due to lobbying). To address this concern, the relationship is re-estimated using the share of top 1% as measure of inequality (instead of family income Gini) and the ratios of 90th/50th and 50th/10th percentiles of family incomes. Generally, the analyses using either imputation or adjustment for family size, or classical OLS vs random effects vs fixed effects, do not change this conclusion.

Income Inequality and Intergenerational Income Mobility in the United States (Bloome 2013) Figure 3

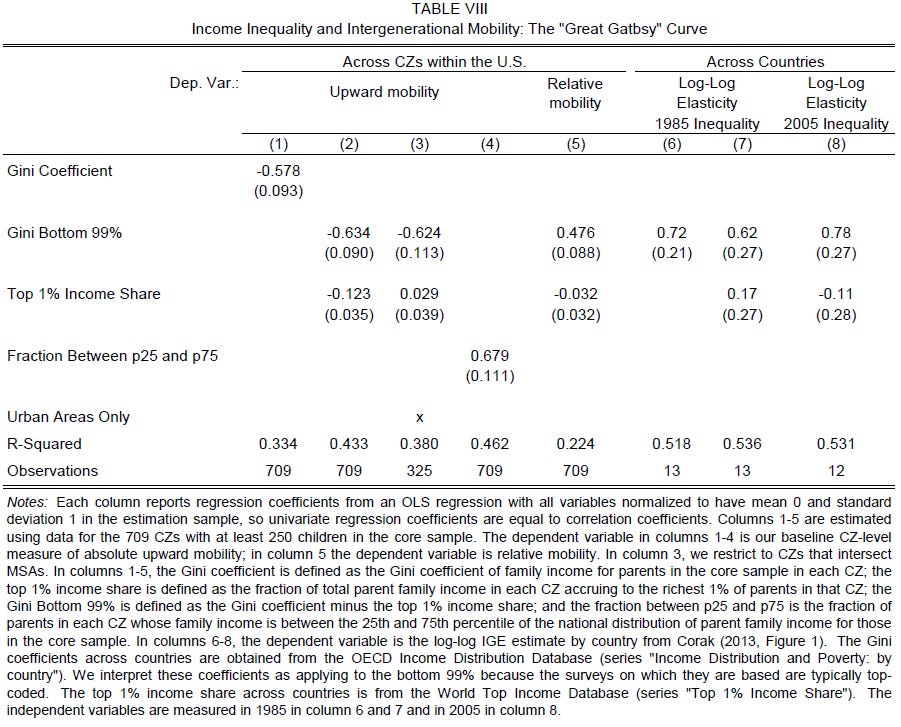
Chetty et al. (2014a, Table 8) show that the log-log elasticity correlates strongly with Gini bottom 99% while it does not correlate with top 1% income share. Within the US commuting zones (areas), the Gini bottom 99% correlates positively with relative mobility and negatively with upward mobility, while top 1% income share shows no obvious correlation. Furthermore, within the US, the income mobility varies greatly across states. This is an interesting pattern since it is known that most income inequalities is due to the top 1% (Piketty, 2014).

Where is the Land of Opportunity - The Geography of Intergenerational Mobility in the United States (Table 8)

Chetty et al. (2014b) study the SOI sample (and tax records data for cohorts during/after 1980s) in the USA for birth cohorts 1970s-1980s/1990s. Using classical OLS regressions, the trends in rank-rank income (children aged 26 and 30) and college attendance (children aged 19) relationships with parental income tend to be flat. The trend in mobility is also flat by Census Division (Pacific, Mountain, New England, East South Central). Using transition matrices method, the probability of reaching the top quintile at age 26 is flat over time (by birth cohorts). This absence of trend surely contrasts with the increasing trend for inequality during the same periods.

3. Statistical artifacts and measurement issues.

As highlighted above, it is unfortunate that most studies did not bother to examine parent-daughter elasticities despite the availability of that data. The absence of gender invariance in US/europe mobility gap indicates there is a strong moderator to be found in the gender variable. Has it been verified that the large gender difference in income mobility in the US is due to self-reporting measure ? Given the study of Dahl & DeLeire (2008), we can conclude it’s not. They use the US data of SIPP, SSA, DER and SER, resulting in 1869 father-son pairs and 1652 father-daughter pairs. The income come from administrative data. The evidence is strong. The elasticity ranges between 0.26 and 0.63 for sons, between 0.00 and 0.27 for daughters. The wide range is explained by model specification and samples chosen. Specifically, more averaging produces higher elasticity, and samples that include fathers who have years with no labor market earnings produce lower elasticity.

How to explain this ? One possibility is that parents tend to favor (by investing more resources) the boys, not the girls. Scarr & Weinberg (1994) adoption/family study provides some evidence of the said hypothesis. It was found that the girls outcome was less predictable than that of the boys based on the family’s characteristics and background. This raises a difficult question. Because if money causes higher mobility, and considering the parents invest more on the sons, this automatically implies that the sons of the lowest quintile families must have higher probability to move upward than do the daughters. We know that, compared to the sons, the daughters have considerably higher income mobility (both upward and downward) in the US, and only modestly higher elasticities in other countries considered in the above studies. Even if it follows the expected pattern, the advantage in resources devoted to the boys is probably not large enough to play a dominant role.

Another possibility, and more predicted one, is simply that women care less about their job career than do men. One reason for this is due to the women’s role of mothering. But this cannot explain why we have a gender gap this large in the US, but not in the other countries. Clearly, something odd is happening in the US.

Perhaps sampling errors may explain the US-Nordic gender difference since the former is based on a small sample size (~3400) whereas the Nordic countries have ~10000-60000 individuals in their data base. N=3400 is large by most standards, in psychology for example. But since we attempt to approximate the population estimates, it is probably low for the US. But the fact that Jäntti has been replicated successfully (Dahl & DeLeire, 2008) with another sample of about the same size renders sampling error much less likely. Thus, none of the possibilities highlighted above is relevant.

Now, concerning methodological issues, a general overview of the pitfalls is provided by Black & Devereux (2010). They warn (pp. 10-12) against lifecycle bias. Studies show that the income elasticities become lower when the age of fathers at measured earnings increases. On the other hand, at any given father’s age, the father-son elasticities increase when the son’s age increases.

The use of the variables has some relevance. Solon (1992) shows in the PSID data that higher estimates are produced when correlating father’s family income with the son’s family income (0.483) instead of father’s earnings with the son’s earnings (0.386). The elasticity was only 0.294 when hourly wage is used. The fact that hourly wages produce lower elasticity than annual earnings has been confirmed in USA (Jäntti et al., 2006) but not in Denmark (Hussain et al., 2009).

Björklund & Jäntti (2000) argue that statistical methods may matter. If income data shows difference in asymmetry (resulting in more mobility (less correlation) at the top than at the bottom or vice versa), then an estimation of income elasticity based on either regression or correlation will be very sensitive to this artifact, and will bias the correlations. They recommend, in light of this, to base the analysis on frequency/contingency tables, and more generally on non-parametric tests. This also applies to the choice of IGC against IGE index.

Hirvonen (2008) shows an alternative method, the quantile regression. It also allows differential effect (i.e., non-linearity) of the independent variable on the dependent at different levels, which is different from a classical regression which gives only the mean effect of the independent on the dependent variable. This may be a reasonable alternative because the higher immobility at the top and bottom (sometimes reported in analyses of transition matrices) may have been due to ceiling and floor effect if upward (downward) mobility is not possible for those born at the top (bottom). Thus, Hirvonen argues that matrices should be splitted into deciles rather than quartiles or quintiles, which seem to be very sensitive to ceiling and floor effects. However, Hirvonen (2008) still found some evidence of greater earnings immobility at the extremities even with the use of deciles, in Sweden at least.

Bhattacharya and Mazumder (2011) also criticize the studies that rely on arbitrary discretizations of the distribution (e.g., deciles, quintiles, quartiles). They suggest a new measure of mobility, namely, the probability that the offspring’s percentile rank in earnings distribution will exceed that of the parents (see pp. 339-340 for illustration). When they use this approach on the NLSY79, they found that the black-white difference in mobility is much less than what is usually reported. Among white (black) men whose family income during their youth was below the 25th percentile, 84% (76%) achieved a higher percentile than their parents, a difference of 8%. Using the quartile approach yields a 26% difference. The small difference of 8% almost disappears after controlling for AFQT score, which means IQ exerts a modest effect.

O’Neill et al. (2007) find that classical measurement error in the child’s future earnings (the dependent variable in a regression) cause biases in mobility. When errors are correlated (i.e., non-classical measurement error), the direction of the bias depends on the strength of the correlated errors in the two variables. Assuming no correlated errors in the two variables (e.g., parent and offspring outcome), measurement error in one variable leads to over-estimate mobility, especially at the tails of the distribution. For example, a probability of 0.481 to stay in the lowest quartile in the case of no measurement error will become 0.446 and 0.406 if reliability (s) is 0.75 and 0.50, respectively. They then compare a situation of no error and a situation with simultaneous measurement error (i.e., both variables) with or without correlated errors in the two variables (Table III). Without correlated errors, mobility rises substantially compared to no error. At any given reliability level, low correlated errors cause an over-estimated mobility whereas high correlated errors cause an under-estimated mobility compared to no error. Interestingly, they note that s=0.50 is typically the reliability estimate for single-year earnings whereas s=0.75 seems to be the reliability for 3-year averaged earnings.

The effects of measurement error and omitted variables when using transition matrices to measure intergenerational mobility (Tables 3-4)

They commented the above table as follows : “Consider the results when s = 0.5. The proportion of sons remaining in the lowest quartile group of the earnings distribution falls from 0.481 to 0.357 when ρuv = 0; the decline in the middle is much smaller (0.296 to 0.263). However, when ρuv = 0.8, the proportion of sons remaining in the lowest quartile group of the earnings distribution rises from 0.481 in the true distribution to 0.569 in the observed distribution; the increase in the middle is smaller, 0.296 to 0.334.” (p. 169). And they conclude that “by changing the error process, it is possible to generate a range of mobility measures consistent with those reported in previous empirical work”. This is important because studies like that of Jäntti (2006) use single-year measures. Their estimates are certainly biased, but toward which direction is a question worth asking.

Another artifact not necessarily well appreciated is assortative mating among the couples. That marital sorting (homogamy) by education increases inequality should be known (Fernández & Rogerson, 2001). When people choose to mate with people of similar social background, this creates a positive correlation between the parents’ education, occupation, and perhaps, personal earnings. This, in turn, will improve the parent-offspring correlation, and helps to maintain social immobility. Ermisch et al. (2006) inform us that 30% and 50% of the couples in Britain and Germany have equal educational levels. In this case, the parent-offspring correlation with regard to SES measures (an occupational prestige (H-G) score based on Hope-Goldthorpe technique) is upwardly biased for Germany, relative to the UK. In their study, for both men and women in both countries, 40-50% of the covariance in parent-offspring income could be attributed to the person to whom one is married. They have thus succeeded to replicate Chadwick & Solon (2002) study that has used the PSID data for the US. They have found evidence that the spouse (of the offspring) earnings was as elastic as the offspring own earnings with respect to the parents’ income. Hirvonen (2008) succeeds to replicate Chadwick & Solon (2002) in a swedish administrative data set for income. This can be observed in Table 2 below, which gives the numbers for women, where the elasticity for the couple (Ew+Eh) earnings is virtually identical to that for the husband (Eh) earnings. The difference in elasticity is greater for men but not wide. Certainly, the theory underlined behind the Great Gatsby curve is strongly attenuated.

Intergenerational Earnings Mobility Among Daughters and Sons - Evidence from Sweden and a Comparison with the United States (Hirvonen 2008) Table 2

Marks (2013) cites a study by Hobcraft (2001) which reports elasticities ranging from 0.10 to 0.33 for the 1958 NCDS cohort (UK data). The intergenerational correlation for men’s income and that of their family of origin is 0.21 and for women 0.11. For father’s and son’s income the elasticity is higher at 0.30 but father’s and daughter’s lower at 0.15. For males, the elasticity is lower for family income than for father’s income. The elasticities between male incomes and their partner’s family’s income (or father’s earnings) is comparable to that for their own parents’ income or father’s earnings, suggesting that assortative mating appears as important as the economic resources of the family.

The question of assortative mating is important to the US exceptionalism. If Murray (2012) is correct about the cultural stratification that is actually occurring, we must expect a growing cultural stratification with regard to mating. This will indirectly strengthen social stratification with regard to mating. At the same time, it is also possible that inequality could produce in itself a greater likelihood of assortative mating which, in turn, should increase social inequalities, and the process snowballs itself. One reason to suspect higher spousal correlation with respect to SES, in the USA, is suggested by what Tammi (2013) discovered about american people attitude. In Sweden the support for redistribution increases as the belief that hard work brings success declines, while in the USA, it was just the opposite. The definite proof is given by Raaum et al. (2007, Tables 2 & 4) where it is shown that the degree of marital sorting is the highest in USA, followed by the UK, compared to Denmark, Finland, and Norway (interestingly, Norway has a stronger income elasticity and assortative mating compared to the two other Nordic countries). They find that elasticity among married women (relative to her parents income) when measured with their own earnings is similar across these countries, but elasticity is way stronger in UK and US when measured with either the husband’s earnings or the family earnings (wife+husband). Single (unmarried) women in US (0.435) have larger elasticities than in UK (0.382) and Nordic countries (0.266, 0.169, 0.192). For men, the elasticity is always much stronger in US than in Nordic countries, except for married men (relative to his parents income) when measured with the wife’s earnings. Raaum et al. (2007, Tables 5 & A-3) also find that having children decreases the women’s probability of working full time, but more in UK and especially in US than in Nordic countries, as seen in the large child*earnings interaction (-0.255 and -0.180) for US wives (variable : earnings of the husband’s parents) but weak child*earnings interaction (-0.068 and -0.004) for US married women without children (variable : earnings of her own parents). Thus, children fully mediate this effect in the US. As for the explanation, the authors argue (pp. 35-37) that married american women respond to the higher income level of the husband by withdrawing from the labor market more frequently than would do european (e.g., Nordic) women, and this is worsened by the fact that the wage penalty for being part-time worker, instead of full-time worker, is stronger in US and UK than in Nordic countries. On the other hand, they explain that the advantage in quality and availability of child care services in Nordic countries probably make the parents more willing to leave the children with professional child-care workers. If the US system encourages women to work more, then, their earnings will match more closely their husbands, creating a higher elasticity in the US under the effect of increased marital sorting. The works of Raaum and colleagues also tell us that IGE/IGC estimates can differ for the US, depending on which income (own, spouse, family) we use.

As argued above, income, education and occupation reflect a common factor but also have an independent variance that is specific to each of them. Blanden (2013) noted the increasing immobility of the UK with regard to income even though the social class mobility was left unchanged. That may be explained if we conceive the idea that income differences within social classes are passed on to the offsprings. Blanden (2013) also reports appreciably higher father-offspring correlation in the US than in the Nordic countries, Germany, Netherlands, or UK, in years of schooling. The variable is all the more objective but may not have the same meaning across countries. Even within countries, the same years of schooling in a poor and in a rich neighborhood may have different meanings.

But it should be noted that income is a sub-optimal measure of SES. Unlike education and occupation level, which depend more on one own’s ability, the income itself may depend somewhat on the talent or in rare cases on sheer luck. For this reason, income is probably transmitted to the children less easily than education, either environmentally or genetically. The evidence is provided indirectly by Marks (2013, pp. 350, 355) who wrote “Contrary to popular conceptions, the inheritance of wealth has little to do with income inequalities. Jencks et al. (1972, p. 214), citing the findings from a 1960 survey, point out that inheritance plays an extremely limited role: 80% of families inherited nothing, a further 14% inherited very little and only 1% of families inherited enough to substantially boost their income”. He also cited Jencks et al. (1979) review of the earlier studies on sibling intra-class correlations (ICC). If family background has less effect on earnings than on education, then it is expected that the sibling ICCs will be lower for income (0.13-0.21) than for education (0.53-0.55) and occupation (0.31-0.37). This was expected because income has much more variability more over time and is thus more subject to lifecycle bias. Since any difference in family background is held constant, sibling resemblance will be either due to shared environment or genes or both and sibling difference will be either due to non-shared environment or genes or both. This is because the genetic correlation (0.50) of the siblings is only an average with a normal-curve distribution (Visscher et al., 2006). Given the low sibling ICC for income, it can be inferred that income is a poor measure of family background. Note however that Marks (2013) did not mention if these correlations are corrected for measurement error or not.

Björklund et al. (2002, 2004b) and Schnitzlein (2014) report correlations that are way stronger than those reported by Marks (2013), thanks to averaging being a better approximate to permanent income. The rationale for this practice is that income has both a permanent and transitory component, and the latter needs to be purged. What is called permanent income has been criticized by Muller (2010) who demonstrates that elasticity is higher when parental income is measured during the time of the child’s birth and following years than during non-childhood period. Not all years are equally important. The corollary is that averaging around years of importance inflates the estimates due to effects of serial correlation in income measures. But a more serious problem reported by Muller (2008, 2010) is that averaging ignores the impact of transitory income in intergenerational mobility, the impact of which is stronger for poor countries and areas. Elasticity is therefore more underestimated among the more deprived areas. He finishes with “Averaging therefore biases tests toward the null that income matters equally in all periods (and therefore that transitory income does not have causal significance).” (p. 294).

Björklund & Chadwick (2003) use the large swedish administrative data, and report a (log) labor income elasticity (biological father-son) of 0.25 for sons living always with their biological fathers (N=28926) and an elasticity of 0.20 for sons living always with their nonbiological fathers but never with their biological fathers (N=627), of 0.04 for neither (N=297), of -0.02 for sons living sometimes with nonbiological father but never with biological father (N=957). Those numbers do not square either with a purely genetic or purely social hypothesis. And because the null correlation for sons living without father should not be taken as a sign of increased mobility, this suggests that a given country having substantially more children living without fathers will have under-estimated elasticity. That appears to be a strong assumption. But if there is trend toward higher (lower) children living without father, then, the more recent cohorts will show under-estimated elasticity.

Hauser (2010, pp.12-13) points out that women typically exceeds men in occupational and educational level but men exceeds women on income. This adds even more questions about the relevance of income variable. Due to this, the SES index measures based on the sum or aggregation of all these measures do not account accurately for gender differences. This is illustrated even further by his study where he finds in the GSS sample (for US) that women have reduced educational stratification but not occupational stratification. As expected, women may have improved their educational level but at the time they give birth, they experience a stagnation in their career. Perhaps for this reason, Blanden (2013) prefer the use of fathers’ status rather than that of the mothers because of their role to give birth, they sometimes do not contribute much to the family incomes.

To summarize, education variable has more advantages than income and occupation (especially for women) and father’s SES is a better measure than mother’s SES (although it may not be unreasonable to combine them). But while it is certain that some portion of these variables is specific to them and not shared together, they also measure different dimension of the social status, one must first ask about the causal pathways. The reason why education should be preferred against income is that education causes income more than the reverse. And, as we will see, the impact of education is partly mediated by IQ.

4. And if America is less mobile : Entering genoeconomics.

Suppose we admit the plausibility that mobility is less in the US for the poorest income levels, which may not be a surprise, at first glance, considering that welfare system are supposed to help the poor to move upward, we must ask if the lower propensity of the America to redistribute the money is greatly responsible for the higher income immobility. Otherwise, any discussion on this topic has no relevance at all.

An important factor usually ignored by the economists is genes. That is not a surprise considering that most people dislike the idea of genetic factors, and social scientists have a strong preference for socialization theories. Unfortunately for this ideology, the evidence for genes is rather strong.

Björklund et al. (2005, p. 161) examined a large twin samples from Sweden, the STR survey, which has ~4400 MZ(T) twins, ~6800 DZ(T) twins, ~91000 full siblings reared together and still several thousands of half-siblings reared together or apart. Their variable is the annual labor earnings, the data come from compulsory reports by employers to tax authorities (Statistics Sweden). Their model is a classical one that allows the partitioning of a phenotypic trait into its genetic and environmental components, as follows, Y=G+C+E, where G is genes, C shared-family effect common environment, E environment unique to the individual and not shared through the family, and Y the outcome variable of interest. Since these components must add up to 100, the rise in one of these components must be accompanied by a decline in other component(s). This simplistic equation assumes no correlation between G and any type of environments. If (positive) GE correlations were to be found, genetic effect is said to be over-estimated. This, however, assumes that environment causes genes and not the reverse. Several models with different assumptions are fitted to the data. Model 1 assumes the genetic correlation of 1.00 for MZ twins, of 0.50 for DZ twins and full siblings, of 0.25 for half-sibling, of 0.00 for adoptive siblings. These figures are the expected values assumed in all behavioral genetics research. Model 2 allows a correlation between G and C, which turns out to be a (very) small negative for both brothers and sisters. Model 3 assumes the genetic correlations not to be equal to the expected values in model 1, and thus are freely estimated, at 0.43, 0.25, 0.14 for brothers, 0.39, 0.26, 0.18 for sisters, regarding DZ and full siblings, half-siblings, and adoptive siblings. Model 4 allows the C parameter not to be equal for all pairing groups. The Equal Environment Assumption (EEA) posits that MZ will not be more similar than DZ with regard to shared environments which in turn would have caused an increased similarity with respect to the phenotype. In this situation, the heritability will be confounded with shared environment. As shown by its (lowest) Chi-square statistics, model 4 displays the best fit (approximation) to the data, followed by model 3, model 2, and finally model 1 which has the worst fit. Obviously, the Chi-square is sensitive to sample size, and is not a good statistics for model fitting. However, the difference in effect sizes justifies model 4 as the best fit, as the cross-sibling correlation of C is 0.406, 0.461, 0.209 for brothers, and is 0.282, 0.340, 0.254 for sisters, with respect to DZ twins reared together, non-twins reared together, and siblings reared apart. The departure of DZ cross-correlation with MZ (equal to 1) is a very serious one. Thus, EEA is violated. This is curious considering that a rejection of EEA with respect to any behavioral trait is the exception, not the rule. In model 4, it was estimated that 60% and 50% of variance in earnings correlations is due to genetic factors, with respect to brothers and sisters, respectively, for the entire sample.

It is possible to quantify the impact of non-additive genetic effect specifically for the twin sample. Since a simple additive model predicts MZT correlation to be twice DZT correlation, with a positive MZT>2DZT giving a proof of non-additive (dominance) effect, if we take the numbers in Model 4, there is a modest departure from a perfect equality, as 0.363-2*0.166=0.031 and 0.309-2*0.116=0.077. Dominance is indeed modest. These estimates are variance-based, and add up to 100. Since the correct effect size is not r² but r, they must be square rooted. In sum, inequality is best explained in terms of genes, and non-shared environments. This has dramatic consequences for public policies because the main assumption behind their intervention is that most environmental effect runs between families, not within. For most behavioral traits, shared environment is weak in adulthood. Income is not an exception. Twin heritability can be obtained by doubling the difference between MZT and DZT. In this case, heritability is 0.394 for men and 0.386 for women, and the rest is due to non-shared environment.

For the same data set, Benjamin et al. (2012) report the sibling correlation for log income averaged over multiple years, for twins aged 1, 3, 5, 10, 20 years-old. For men, we have 0.406-2*0.164=0.078, 0.513-2*0.193=0.127, 0.512-2*0.201=0.110, 0.556-2*0.241=0.074, 0.626-2*0.270=0.086, for years 1, 3, 5, 10, and 20. For women, we have 0.266-2*0.143=-0.020, 0.293-2*0.137=0.019, 0.297-2*0.198=-0.099, 0.353-2*0.226=-0.099, 0.481-2*0.221=0.039, for years 1, 3, 5, 10, and 20. Most values are positive, and thus give evidence for non-additivity. These values, however, are small. The near-absence of shared environmental factor is confirmed once more. With regard to heritability estimates, the authors remarked that heritability increases from 0.37 to 0.58 in men as we move from single-year income to a 20-year average. The corresponding figures for women are 0.28 and 0.46. Thus, averaging can still increase heritability even in the absence of measurement error.

Similarly, Hyytinen et al. (2013) showed, using the Older Finnish Twin Cohort Study for Finland, with MZ and DZ pairs of 620 and 1146 for women and 494 and 1094 for men, that 24% and 54% of variance in lifetime income for women and men, respectively, is due to genetic factors, whereas shared environment is small. The authors begin to cite studies showing that schooling reforms have enhanced earnings mobility. As explained above, this is irrelevant due to its weak intergenerational transmission through the family.

The income data was from administrative registers and thus do not suffer measurement errors due to misreporting. For their analysis, they use the Defries-Fulker regression method, which can be formulated as INC1=β0+β1INC2+β2R+β3(INC2*R)+ϵ, where INC is income, β0 is the intercept, β1 is a measure of shared environment (C), β2 is a coefficient of genetic relatedness (r=1.00 for MZ and r=0.50 for DZ twins, and thus assumes full additivity), β3 the heritability, ϵ the error term (E) which includes both the non-shared environment as well as measurement error. It is possible to include a parameter for non-additive genetic effect, or dominance (D), which in this case can be denoted as β4(INC2*D), where D=1.00 for MZ and D=0.25 for DZ twins. This can be called the ADE model, where β3 and β4 evaluate the additive (i.e., narrow) and non-additive heritability for income. The sum of the additive (A) and non-additive (D) is called the broad-sense heritability. Thus the difference between ACE and ADE models is that the former, but not the latter, assumes the heritability is purely additive.

Heritability of Lifetime Income (Hyytinen 2013) Table 3

We read the results from their model fitting in table 3. For females, shared environment (C) is small (0.10) in the ACE model whereas for males the C parameter is negative and this is indicative of dominance (D) effect, since C is the mirror of D, and conversely. For both gender group, based on the model fit index Akaike (AIC) the AE has the worst fit but the ACE and ADE have equal fit. At first glance, one believes it is impossible to select among them. However, given that D is negative for women, this model is probably ill-specified and thus they have (rightly) opted for the ACE. Because C is negative in ACE and this in turn is suggestive of large D parameter, which is confirmed in ADE model, the authors have correctly chosen the ADE as the preferred model for men. In the ACE, women and men have a heritability of 0.24 and 0.77. In ADE, the A and D parameters for women amount to 0.54 and -0.20 and for men to 0.07 and 0.47. The sum of A and Z gives a broad heritability of 0.54 for men. Given that ACE should be preferred for females, their heritability is 0.24. Interestingly, they note (table A2) that the use of a broader measure of income (which includes capital income and transfers, such as unemployment benefits and parental leave benefits) has improved the heritability estimates, which were 0.42 and A+D=0.26+0.33=0.59 for women and men, given their respective preferred model, AE and ADE. This provides another illustration of how measurement errors can reduce heritability.

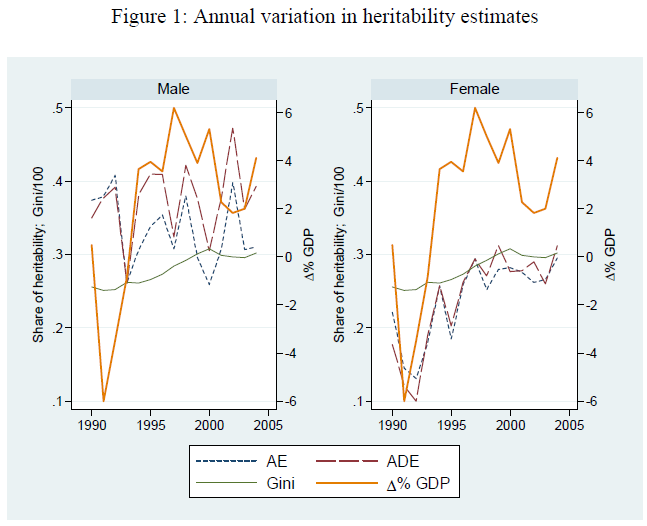
When they attempt to add education as covariate in the regression, thus holding education constant, the parameter estimates (A,C,D,E) remain somewhat unchanged compared to table 3, even though heritability has diminished somewhat. When education effect is deducted from income, the A, C, D and E parameters appear similar. When they use as dependent variable the annual age-adjusted income instead of lifetime income, as depicted in figure 1, male heritability is stable during 1990-2005 at around 0.30 and 0.40 but not only female heritability is lower but varies greatly over time, being as low as 0.15 in 1990-1995, and increasing from 0.20 to 0.30 between 1995 and 2005. Typically, they found that heritability trends correlate with GDP growth for women only. Finally, they find that income uncertainty (defined by its standard deviation) has a heritability of 17% (AE) for women and 35% (ADE) for men.

Heritability of Lifetime Income (Hyytinen 2013) Figure 1

These figures for Scandinavian countries are relevant considering that heritability estimate is dependent on a particular environment. If environments do not vary across the population studied, thanks to the success of public intervention to equate environments for all social classes, the remaining variance must be attributed to heritability and will come much closer to 100% to the extent that genetic is the only portion that continues to vary and there is much less opportunity to equate the environment. Thus, it may be expected that income and/or social status is less heritable in the US. Rowe et al. (1999) examined the sibling groups in a US survey data, the NLSY79 (28-35 years old, 1943 full siblings, 129 half-siblings), with unemployed people removed for the analysis. The heritabilities for IQ, education (in 1992) and income (in 1992) were 0.64, 0.68, and 0.42, in the best fitted model. Because the study deals with siblings and no twins, the EEA is not relevant. At first glance, the income heritability is not different from the estimates in Sweden, but since the self-reported income (for US) must have lower reliability than income from administratve register (for Sweden) the heritability in US is somewhat under-estimated. This is especially true if they use only 1-year measure (1992). But unless reliability of income is incredibly low, we will not expect heritability and/or shared environment estimates to be severely biased downward. Finally, Rowe and colleagues (1999) report that “The majority of the total genetic variation in IQ (55%) and education (75%) came from the common genetic variable, with the rest coming from the specific genetic factors. In contrast, the majority of the total genetic variance for income came from the specific genetic factor (71%). The common shared environmental factor accounted for 0.08 of the variance in income, 0.18 in education, and 0.23 in IQ. Specific non-shared environment was a relatively small component of IQ and education variation (0.13 and 0.14, respectively), but was a substantial component of income variation (0.49).” (p. 418). This, again, proves that not only income poorly reflects the family’s social position but also that family environment has only a modest effect on income, in accordance with past twin studies in the US agreeing with an income heritability of 50% (Rowe, 1994, pp. 137-141). Generally, the heritability estimates for income are around 0.40 in Nordic countries, and perhaps 0.50 in the US.

The greater environmentality of education relative to income found in the US is replicated in an australian twin study (Miller et al., 1995), with pairs of MZ=602 and DZ=568, mean age=36. Given MZ and DZ correlations of 0.776 and 0.527 for education, the heritability is 0.498 and shared environment is 0.278. Given MZ and DZ correlations of 0.680 and 0.321, the heritability is 0.718 and non-additive (dominance) effect is 0.038. Similarly, Ashenfelter & Krueger (1994) examine the Census data CPS for the United States. There were 298 MZ and 92 DZ twins, aged 36. Given MZ and DZ correlations of 0.563 and 0.364 for income (hourly wage rate), heritability is 0.398 and shared environment is 0.165. Given MZ and DZ correlations of 0.658 and 0.543 for education, the heritability is 0.230 and shared environment is 0.428. Using a danish twin registry, the MADT, 330 female MZ and 291 female DZ twins, Rodgers et al. (2008) estimated the heritability of a 5-scale IQ and education at (respectively) 0.52 and 0.48. The respective numbers for shared environment are 0.02 and 0.25. Silventoinen et al. (2004) give the MZ and DZ correlations for education, in the Finnish Twin Cohort Study (FTCS), of 0.83 and 0.59 for men, of 0.85 and 0.62 for women. Thus, the heritability for amounts to 0.48 (men) and 0.46 (women) and the shared environment amounts to 0.39 (men) and 0.35 (women). The exact number of pairs for twins having data on education is not given but is probably no more than ~2400 MZ and ~5000 DZ. Latvala et al. (2011) examine a sample of 4858 twins in Finland, the FinnTwin16 from the FTCS survey, having education data. For females, the ACE components are 0.32, 0.30, 0.37. For men, 0.41, 0.28, 0.31.

The few existing adoption studies summarized by Black & Devereux (2010, Table 3-B) produce lower estimations of shared environment. Das & Sjogren (2002) report that father’s education was not correlated with either the adopted or biological children future income. Father’s income was correlated negatively (-0.244) with adopted children and positively (0.288) with biological children future income. The data set (126 adopted, 141 biological) comes from Scarr & Weinberg (1978, Table 5) where no family effect was found for IQ. The mean age of adoption was 2.6 months. And the absence of any range restriction regarding environmental factors (e.g., education, income) is an indication that it is a strong, reliable data. Sacerdote (2007, Tables 4, 5, 8) reports shared environment of about 0.150 and 0.110-0.140 for education and income. The respective numbers for heritability were 0.400-0.440 and 0.330. The (adoptive) mother-child correlations for education and income were 0.090-0.100 and 0.186 whereas the respective correlations for biological child were 0.300-0.310 and 0.246. The sample sizes were ~1310-1360 and ~550-570 for adopted and biological children, respectively. The adoptions took place in infancy. And the fact that the variance in family environment is no less than what is observed in the US population indicates the absence of range restriction that could under-estimate the effect of shared environment.

Björklund et al. (2004a) use a (swedish) population register data set of adopted children (N=7498 having education data, N=5895 with income data) and biological children (N=148496 having education data, N=115000-122000 with income data). To the extent they were using population data set, range restriction with respect to environment appears unlikely. They select a sample with minimum age=30, the mean (and maximum) age of adoption was 1.8 (and 7.5), with age of adoptive parents between 25 and 47 (mothers) or 66 (fathers). The correlations given in Table 3 (columns 1-2 and 4-5) were modest for adoptive fathers or mothers with adoptees (years of schooling =~0.120, college education =~0.100) but substantial for biological children (years of schooling =~0.290, college education =~0.270). The correlations given in Table 4 were modest for adoptive fathers or mothers with adoptees (earnings =~0.130-0.140, total income =~0.150-0.160) but substantial for biological children (earnings =~0.230-260, total income =~0.230-260). We also notice that the correlation of family income/education with that of the biological sons is stronger than with biological girls. However, this gender effect is not present for the adoptive children. When they restrict the sample to children aged 0-1 at adoption, the correlations in tables 3-4 and 6 were quite comparable, and the interaction between adoption age and parental outcome variable(s) is just zero. Their test for linearity seems to hold. This study has an advantage in that it was possible to test the hypothesis that the parents have treated the adopted and biological child differently. But the similarity in the sibling correlations (Table 7) between adoptees and biological children (N=1036 for years of schooling, and N=696 for total income) and adoptees reared in the same adoptive family (N=336 and N=265) suggests this assumption would not be accepted. Adoption within-family (e.g., stepchildren) can downwardly bias heritability but they argue (pp. 12-13) this problem seems unlikely to their data. However, selective placement seems to have taken place. The income and education variables for the adoptive and biological parents were modestly correlated (0.117-0.144). Adoption studies need a strong assumption : random assignment. This can be easily violated. The worst-case scenario is when the more intelligent and rich families have selected the children or infant with best endowment (Spitz, 1986). The child’s genes and the adoptive family environment will thus be confounded and correlated (GE effects). Furthermore, the impact of heritability can be biased upward because the genetic endowment of the adoptees and adoptive parents will also be correlated. The condition is fulfilled if the background of the adoptive family is correlated with that of the biological family. In the above cited studies, random assignment appears to be met.

As we see, adoption studies are powerful tools in that they also provide a direct test of the hypothesis that income elasticity is due (partly) to genetic factors. A lower parent-offspring correlation is sufficient in this regard to prove the genetic hypothesis. Björklund et al. (2006, Table 2) re-use their swedish population register data on biological (~87000-94000) and adopted children (~1800-2100) having a mean age of 35 years. Regarding the adoption design study, the adoptive parents are more educated than the biological parents. Supplied with tax-register data, they found once again a strong genetic effect. For years of schooling, biological parent-offspring correlation was ~0.240 for years of schooling and 0.235 for earnings and 0.241 for income. For the adoption design, the biological father/mother and adoptive father/mother have correlations (with the adopted children) of 0.113/0.132 and 0.114/0.074 for years of schooling, of 0.047 and 0.098 for earnings, of 0.059 and 0.172 for income. The biological parents indeed show less resemblance with their adopted-away children but the adoptive parent-offspring correlations are still lower than the biological parent-offspring correlations. Regardless, the key finding is that a large portion of the income elasticities can be explained by genetic factors. One detail however. The weak difference in correlations for income between biological parent-offspring (0.172) and adoptive parent-offspring (0.241) contrasts with the large difference (0.235 vs 0.098) when earnings instead is used. Liu & Zeng (2009) suspect the reason is due to the fact that their income variable “include income from both work and self-employment” and which ultimately “depends not only on an individual’s ability, but also on the amount of utilized capital. As capital can be easily transferred from one generation to another independent of genetic link, it is not surprising that including income from self-employment increases the intergenerational earnings elasticity for adoptive children”. This again illustrates the importance of the variables in use.

Liu & Zeng (2009) examined biological (4158, and 1853 fathers) and adopted children (121, and 93 fathers) in the PSID survey (US) with self-reported income. The labor income elasticities for biological father-child are 0.345 and 0.369 with respect to father’s (hourly) wage and (annual) earnings. The respective correlation coefficients for adoptees (i.e., the interaction term adopted status * father wage or earnings) are -0.231 and -0.273 lower, which gives elasticities of 0.113 and 0.096. Since a correlation is expressed in standard deviation, we can easily translate the effect size in percentage, so that 1% increase in father’s wage (earnings) raises the biological and adopted child’s wage (earnings) by 0.345% (0.369%) and 0.113% (0.096%). Restricting the sample to individuals aged 30+ gives elasticities of 0.386 and 0.395 for biological child, of 0.168 and 0.052 for adopted child. Later age of adoption can be suspected to lower the parent-offspring correlation. But when they restrict the sample to age (at adoption) before 5 years old, which now becomes 70, the correlations for those adoptees were -0.304 (wage) and -0.328 (earnings) lower, which gives elasticities of 0.041 and 0.041. It was not possible to test the assumption of selective placement, but at the very least, they have tested the possibility that the parents could decide to adopt children from their relatives. If that happens, the genetic link between the adoptees and adoptive parents is positive, and this will bias upward the parent-offspring correlation for adoptees, resulting in an upward (and downward) biased estimate of shared environment (and heritability). This also applies to the Björklund studies. When they restrict the sample to adoptees who do not have any relationship with their adoptive fathers before adoption, the interaction between adopted status and father’s wage (or earnings) is -0.312 (or -0.463). They have explained that some children (40%) had genetic link (e.g., stepchildren) with the adopted parents. The coefficient of the interaction is here much larger, and suggests indeed that the genetic contribution to income elasticity has been under-estimated. Interestingly, this genetic contribution is way larger for men than for women. Family size has no impact on the difference in adopted-biological child correlations.

But several studies provide some light of optimism. In a large sample of norwegian twins and their families, Heath et al. (1985) applied model fitting and find that a model allowing for genetic additivity (A or h), non-additivity (D), and familial shared environment (C), but no environmental transmission from parent to offpsring (i.e., passive GE effect), and sex differences in parameters, provides the best fit to the data. For male twins born between 1940-1949, h=0.70, d=0.50, c=0.29, and for 1950-1960, h=0.52, d=0.63, c=0.45. For female twins born between 1940-1949, h=0.67, d=0.00, c=0.64, and for 1950-1960, h=0.53, d=0.32, c=0.71. These values are the correlations and must be squared to obtain the variance (e.g., h² and c²) although the correlation itself is the best effect size. Among males, 74% and 67% of the variance in education is due to broad genetic factors for the two successive cohorts. But for females the broad heritabilities were only 45% and 38%. The shared environment account for 8% and 20% in the variance of education among males in the two successive cohorts. The respective figures for females are 41% and 50%. Over time, there is an indication that heritability declines and shared environments become much more important. This trend is unexpected, because if environments have become more equalized over time, heritability would rise and environment would shrink. Tambs et al. (1989) examined a norwegian sample of MZ (507) and DZ (575) twins, in four successive cohorts, 1931-35, 1944-50, 1951-57, 1958-60. With respect to occupation, education and IQ, the heritability, shared and non-shared environment vary greatly, as depicted in their figure 1, probably due to sampling error. But they are typically estimated as 0.43, 0.51, 0.66, respectively.

Similarly, Johnson et al. (2010) examined the swedish twin data MGR (MZ=3740, DZ=4422) and the US twin data MTFS (MZ=411, DZ=430). As illustrated in table 3, with respect to IQ, the ACE components were 0.58, 0.26, 0.16, for Sweden, and were 0.73, 0.07, 0.20, for United States. In Sweden, shared environment is stronger. Regarding educational attainment, a curious pattern emerges in the ACE raw components (i.e., raw, because they are not standardized and thus do not add up to 100). For low (-2SD) medium (0SD) and high (+2SD) IQ levels, and for Sweden, heritability was 0.31, 0.50, 0.73, shared environment was 0.13, 0.25, 0.42, non-shared environment was 0.21, 0.25, 0.29. But for the US, heritability was 0.16, 0.35, 0.64, shared environment was 0.96, 0.39, 0.07, non-shared environment was same, 0.26, same, (i.e., “same” indicates no difference from the variance at the mean level). The US result needs further replication but, as it stands, familial background has a strong impact on education for low IQs in America, whereas the impact of familial background on education is weak at low IQ but meaningful at high IQ level. The authors suspect the difference stems from the access to university which does not speak in favor of the US system.

The high shared environmental impact in some Nordic countries is interesting because shared environment vanishes in adulthood for most behavioral traits, including IQ (Rowe, 1994). It seems unlikely that assortative mating can account for all these high estimates, but it can play some role. If people tend to mate not randomly but according to the similarity of educational attainment (more than their income level) then shared environment will be over-estimated in twin studies because the genetic correlation of MZ is already 1.00 but is only 0.50 for DZ twins. This means that DZ correlation will increase relative to MZ correlation. Given the proof of such effect, it would appear that educational policies may help to buy an education and move upwardly in social status. But whereas differential educational expenditures may matter, the increased availability of resources should be directed only to the children of poor families since otherwise the learning gap will increase (Ceci & Papierno, 2005). Furthermore, as Jensen (1973) noted, learning without improvement in IQ is not indicative of a good understanding of the material that has been taught, as it does not result in consolidated cognitive gains. If true, it may suggest that these persons having benefited the most from educational policies will not necessarily be able to fully transmit this educational gain to their offspring. This places the relevance of public policies into a new light. If otherwise, this suggests education and not income per se is responsible for social (im)mobility.

The lack of proof that shared environment for either income or education is higher in the US, compared to Nordic countries, is a puzzle for the theories behind the Great Gatsby curve. Given the narrower standard deviation in environmental factors, as suggested by a lower inequality and lower elasticity (IGE) in Nordic countries, shared environment should have been stronger in United States, where there is more room for environmental improvement.

At the same time, however, the partitioning of genetic additivity versus non-additivity has not produced conclusive results yet, and it should be considered seriously. If social intervention can impact a behavioral trait through non-additivity, such as genotype-environmental (GE) effect, then even the high broad heritability may not necessarily preclude large improvement in this trait. Hopefully, some methods directly evaluate the additivity portion of heritability.

Trzaskowski et al. (2014) studied a UK sample (around 3000), the TEDS, and find a heritability of SES for unrelated children aged 2 and 7 at about 0.18 and 0.19. They also found a strong genetic mediation (perhaps something between 94% and 56%) in the correlation between SES and IQ, as given by the ratio of genetic correlation to phenotypic correlation. The genetic correlation, which evaluates the magnitude at which a gene found for a given trait will also be found in another, between SES (age 7) and IQ is 1.00 and 0.66 when IQ is measured at age 7 and age 12, respectively. The technique in use was the GCTA, which has been described earlier, and consists in correlating the similarity across hundreds of thousands of SNPs with phenotypic similarity pair by pair in a large sample of (genetically) unrelated individuals, and is aimed to evaluate only the additive genetic effects. Because the method only involves unrelated individuals, it rules out any possible GE correlations and is resistant to EEA. However, because the rare genetic variants, suspected to have large effects, are under studied, the GCTA estimates are usually seen as lower-bound. The technique is relatively new and is only at its beginning of discovery. It is thus too early to draw definitive conclusions regarding GCTA techniques even though they appear very promising and are becoming more and more commonly used. To illustrate, Rietveld et al. (2013) using this same technique find only 2% of variance in educational attainment owing to 3 SNPs. The authors note that “This coefficient of determination R² corresponds to a difference of ≈1 month of schooling per allele. For College completion, the SNP with the strongest estimated effect (rs11584700) has an odds ratio of 0.912 in the replication sample, equivalent to a 1.8 percentage-point difference per allele in the frequency of completing College”. This further provides proof that complex behavioral traits are highly polygenic, i.e., they are determined by a multitude of genes of very small, tiny effects. The genetic contribution to SES has been directly evaluated by Marioni et al. (2014, with supplemental data) in the Scottish Family Health Study (N=~6600, median age=57). The GCTA heritability for IQ (0.29) and education (0.21) and SIMD (0.18) is not negligible if it was the additive effect that is concerned. The genetic correlation was 0.95 for IQ-education, 0.26 for IQ-SIMD, 0.45 for education-SIMD. The SIMD was an environmental deprivation variable, which includes income, employment, health, education, geographic access, crime, housing. The large genetic covariation between IQ and SES certainly challenges Bowles & Gintis (2002) assertion that IQ has weak genetic link to inequality.

The evidence of the high narrow heritability for IQ poses another problem. Rowe (1994, pp. 142-143) says that the children who socially move upwardly (downwardly) have higher (lower) IQs than that of the fathers. If (earlier) IQ causes (future) social mobility rather than the reverse, as implied by Schmidt & Hunter (2004) and Ganzach (2011), that education does not improve the general factor (g) of intelligence as implied by reaction times (Ritchie et al., 2013) and that schooling reform has no impact at all on IQ (Pekkala Kerr et al., 2013), and the vanishing effect of educational intervention, the range of possibilities for public policies becomes even more limited. As illustrated in a discussion by Gottfredson & Deary (2004), IQ has a direct correlation toward health and longevity, independently of SES. Given the problem with multiple regression I have highlighted earlier, the indirect effect of SES->IQ or IQ->SES needs to be disentangled to get the full effect. Given what is said above, the indirect path is more likely to be IQ->SES than the opposite, which means the total effect of IQ (relative to SES) is under-estimated by multiple regression. And although it is possible to improve education somewhat without improving IQ, the gains will be certainly less efficient. Gottfredson (2004) argues that the equalization of health resources will cause inequality to be higher because high SES/IQ people benefit more from the increased availability of resources. For example, most new information about health diffuses through the public media and yet the health disparities and knowledge gaps tend to grow. The fact that reaction time explains the probability of death through records of births and deaths (Deary & Der, 2005) rules out the hypothesis that this correlation is mediated through knowledge and schooling if they do not affect reaction times. It seems likely that the causal factor is intelligence more than education itself. But if the alternative way to avoid social inequality increases is to make resources only available for the poor classes, this may not be well accepted.

Some studies have examined the link between IQ and inequality. Blanden et al. (2007, Tables 3 & 7) argue that IQ may have some relevance in explaining intergenerational income persistence in UK (British Cohort Study). In their multiple regression model, with changes in mobility as dependent variable, the impact of IQ declines substantially when education is added into the model. Personality measures and labour market experience were also included. The model can account for 0.17 of the 0.32 elasticity in income, and of this 0.17, they attribute 0.10 to education and 0.03 to labour market experience. But, the authors seem to say that IQ can operate indirectly through its indirect effect on education, and thus may not have a large direct effect, i.e., the effect of 0.10 attributed to education most likely contain a portion of IQ effects. To be sure, this technique evaluates only the direct but not the indirect or total effect of the independent variables. If the regression coefficient of IQ declines, it could be that (1) IQ causes education, or (2) the reverse, or (3) that both cause each other, or (4) that another omitted variable causes both of them. If (1) is correct, this means IQ has an impact on mobility indirectly through its effect on education. Then its total effect (direct+indirect) will be very different than what is shown by the regression coefficient. Only path analysis or SEM combined with repeated measures over time can disentangle the causal pathways of the indirect effects. Considering the study of Watkins et al. (2007) it may be expected that IQ causes achievement and not the reverse. The proof they have provided in favor of a causal IQ factor is even under-estimated given Rogosa (1980) warnings that a relatively larger stability for any (independent) variable will downwardly bias its causal path, and given Watkins’ figure 3, the stability coefficient was around 0.80 for IQ tests and 0.50 for achievement tests. At the very least, the simple fact that education has a non-trivial direct path toward mobility in Blanden’s study suggests that it is possible to improve mobility by improving education even if it does not achieve that through improvement in IQ.

The question about equalization of opportunity following the equalization of background should be addressed more directly with regard to education. We have an illustration. Blanden (2013, Figure 7) shows there is a negative correlation between income elasticity and education expenditure (see also, Grawe, 2007, Figure 1). However, Blanden adds the following comment : “Grawe (2007) uses state level variation in pupil-teacher ratios and mobility to assess this relationship and finds that states with lower pupil-teacher ratios tend to have less mobility. This finding is also confirmed by Parman (2011) for a more specific setting; improved school access tended to lead to reduced mobility in early-20th century Iowa”. Interestingly, Parman (2011) argues it was because wealthy families benefited more, coherent with Gottfredson (2004) suspicions with regard to health. Concerning these conflicting results, it could be that within-country analyses are not confounded with cross-national differences that may take form into omitted factors, thus highlighting the strong limitation of the latter kind of analyses. Even if the correlation at the national level is not spurious, more money (1) with more regulation (2) will not help to develop better schooling structures. The Scandinavian countries have more about (1) whereas United States have more about (2). That may explain some of the difference in school quality. One problem is that, historically, (1) and (2) have a tendency to grow together. To ask (1) without (2) seems difficult. But the more important question to ask first is what has caused the lack of school access. If less government causes better economic wealth, school access will not be a problem anymore. Thus, regulation is the problem here.

Given the above discussion, if income is influenced by environments of shared type instead of non-shared type, and assuming that public intervention has mostly a shared environmental component, it seems likely that the apparently higher income mobility in Scandinavian countries is best explained by environmental factors other than public policies that differ between the US and Nordic countries. And the impact of public intervention could be even smaller if it constitutes only a portion of shared environmental factors, and this portion can be either small or large. On the other hand, the impact of shared environment on education is not negligible, and this implies that the impact of public intervention can be more effective.

Leaving the topic of genoeconomics aside, other explanations, if not likely candidates, help us to understand unexpected outcome we would not see otherwise. For example, money manipulation due to bank regulation, according to the ABCT model, can play a role. An illustration is given by the fact that housing price shows usually the highest increases following monetary expansion. But when housing price increases, the poorest workers will not have the ability to move and in this case the employers can charge lower pays without the workers being able to discriminate between the employers’ offer due to their reduced geographic mobility (see my earlier article). The effect of monetary expansion can take another and more insidious forms. To illustrate, the pension system in the US for the retired people relies on pension funds, and this is why it is sensitive to economic crises and boom-bust phases. Another but more plausible candidate is the growing cultural divide noted by Murray (1984, 2012) with regard to the lack of responsibility among the US poor classes. This has been generated partly by the US welfare systems. But apparently this problem is less apparent among the Scandinavian countries where the incentives are much greater. Just because inequality coincides with (im)mobility does not justify hasty conclusions. The unintended consequences of state regulation needs to be well understood, firstly. True enough, the common sense tells us that generous welfare system, everything else constant, should help the poor to move upward. This assumes we predict no unintended consequences. Even with this condition fulfilled, we must quantify the effect of the redistribution on the upward mobility.

It is premature to conclude that the apparent immobility of the U.S. is mostly due to its lack of generosity in terms of redistribution. The causal factors are unlikely to be related to genes but it is also apparent that the kind of social environments responsible for the national differences in social mobility is not necessarily well understood.

5. References.

Ashenfelter, Orley, & Krueger, Alan (1994). Estimates of the Economic Return to Schooling from a New Sample of Twins. American Economic Review 84,5:1157–1172.
Benjamin, D.J., Cesarini, D., Chabris, C.F., Glaeser, E.L., Laibson, D.I., Gudnason, V., Harris, T.B., Launer, L.J., Purcell, S., Smith, A.V., Johannesson, M., Magnusson, P.K.E., Beauchamp, J.P., Christakis, N.A., Atwood, C.S., Hebert, B., Freese, J., Hauser, R.M., Hauser, T.S., Grankvist, A., Hultman, C.M., and Lichtenstein, P. (2012). The Promises and Pitfalls of Genoeconomics. Annual Review of Economics 4: 627–662.
Bhattacharya, D., & Mazumder, B. (2011). A nonparametric analysis of black-white differences in intergenerational income mobility in the united states. Quantitative Economics, 2, 335–379.
Björklund, A. & Jäntti, M. (2000). Intergenerational mobility of socio-economic status in comparative perspective. Nordic Journal of Political Economy 26(1), 3–32.
Björklund, Anders, Eriksson, Tor, Jäntti, Markus, Raaum Oddbjørn, & Österbacka Eva (2002). Brother correlations in earnings in Denmark, Finland, Norway and Sweden compared to the United States. Journal of Population Economics 15: 757-772.
Björklund Anders, & Chadwick Laura (2003). Intergenerational Income Mobility in Permanent and Separated Families. Economics Letters, 80, 239-246.
Björklund, Anders, Lindahl, Mikael, & Plug, Erik (2004a). Intergenerational Effects in Sweden: What Can We Learn from Adoption Data?. IZA Discussion Paper No. 1194.
Björklund A., Jäntti M., Raaum O., Österbacka E., Eriksson T. (2004b). Family structure and labor market success: the influence of siblings and birth order on the earnings of young adults in Norway, Finland, and Sweden. In Corak M (ed.), Generational mobility in North America and Europe. Cambridge University Press, Cambridge, pp 208–225.
Björklund, A., Jäntti, M., & Solon, G. (2005). Influences of nature and nuture on earnings variation. In S. Bowles, H. Gintis & M. O. Groves (Eds.), Unequal Chances: Family Background and Economic Success. princeton. NJ: Russell Sage Foundation Press, Princeton University Press.
Björklund, A., Lindal, M., & Plug, E. (2006). The origins of intergenerational associations: Lessons from swedish adoption data. Quarterly Journal of Economics, 121(3), 999–1028.
Black, Sandra E., & Devereux, Paul J. (2010). Recent developments in intergenerational mobility. Discussion paper series, Forschungsinstitut zur Zukunft der Arbeit, No. 4866.
Blanden Jo, Gregg Paul, & Macmillan Lindsey (2007). Accounting for Intergenerational Income Persistence: Noncognitive Skills, Ability and Education. Economic Journal 117: C43-C60.
Blanden Jo (2013). Cross-country rankings in intergenerational mobility: a comparison of approaches from economics and sociology. Journal of Economic Surveys, vol. 27(1), pp. 38-73.
Bloome, Deirdre (2013). Income Inequality and Intergenerational Income Mobility in the United States. Working Paper. Russell Sage Foundation.
Bowles, S., & Gintis, H. (2002). The inheritance of inequality. Journal of Economic Perspectives, 16, 3−30.
Bratsberg, B., Røed, K., Raaum, O., Naylor, R., Jäntti, M., Eriksson, T., & Österbacka, E. (2007). Nonlinearities in intergenerational earnings mobility: Consequences for cross-country comparisons. Economic Journal, 117(519), C72–C92.
Ceci, S.J., & Papierno, P.B. (2005). The rhetoric and reality of gap closing: When the “have nots” gain but the “haves” gain even more. American Psychologist, 60, 149–160.
Chadwick, Laura, & Solon, Gary (2002). Intergenerational Income Mobility Among Daughters. American Economic Review 92(1): 335–344.
Chetty, R., Hendren, N., Kline, P., & Saez, E. (2014a). Where is the land of opportunity? The geography of intergenerational mobility in the united states (No. w19843). National Bureau of Economic Research.
Chetty, R., Hendren, N., Kline, P., Saez, E., & Turner, N. (2014b). Is the United States still a land of opportunity? Recent trends in intergenerational mobility (No. w19844). National Bureau of Economic Research.
Corak, Miles, Lindquist, Matthew J., & Mazumder, Bhashkar (2014). A comparison of upward and downward intergenerational mobility in Canada, Sweden and the United States. Labour Economics, Available online 30 April 2014.
Couch, Kenneth A. and Dean R. Lillard (2004). Nonlinear patterns of intergenerational mobility in Germany and the United States. In M. Corak, (ed.), Generational income mobility in North America and Europe. Cambridge University Press: Cambridge, pp. 190–206.
Dahl, M., and DeLeire T. (2008). The Association between Children’s Earnings and Fathers’ Lifetime Earnings: Estimates Using Administrative Data. Institute for Research on Poverty Discussion Paper No. 1342-08.
Das, Mitali, & Sjogren, Tanja (2002). The Inter-generational Link in Income Mobility: Evidence from Adoptions. Economics Letters, 75, 55-60.
Deary, I.J., & Der, G. (2005). Reaction time explains IQ’s association with death. Psychological Science, 16, 64–69.
Ermisch, J., Francesconi, M., and Siedler, T. (2006). Intergenerational mobility and marital sorting. The Economic Journal 116(513): 659-679.
Fernández, Raquel, & Rogerson, Richard (2001). Sorting and Long-Run Inequality. The Quarterly Journal of Economics 116, 1305-1304.
Ganzach, Y. (2011). A dynamic analysis of the effects of intelligence and socioeconomic background on job-market success. Intelligence, 39(2), 120–129.
Gottfredson, L. S. (2004). Intelligence: Is it the epidemiologists’ elusive ‘‘fundamental cause’’ of social class inequalities in health?. Journal of Personality and Social Psychology, 86, 174–199.
Gottfredson L. S., Deary I. J. (2004). Intelligence predicts health and longevity, but why?. Psychol. Sci. 13(1):1–4.
Grawe, N. (2007). Primary and secondary school class size and intergenerational earnings mobility. Mimeo, Carleton College.
Heath, A. C., Berg, K., Eaves, L. J., Solaas, M. H., Corey, L. A., Sundet, J., Magnus, P., and Nance, W. E. (1985). Educational policy and the heritability of educational attainment. Nature 314:734-736.
Hirvonen, Lalaina H. (2008). Intergenerational earnings mobility among daughters and sons: Evidence from Sweden and a comparison with the United States. The American journal of economics and sociology 67(5): 777-826.
Hussain, A.H, Munk, M.D. & Bonke, J. (2009). Intergenerational Earnings Mobilities – How Sensitive are They to Income Measures?. Journal of Income Distribution, 18(3-4).
Hyytinen, Ari, & Ilmakunnas, Pekka, & Johansson, Edvard, & Toivanen, Otto (2013). Heritability of Lifetime Income. HECER, Discussion Paper No. 364.
Jäntti M, Bratsberg B, Roed K, Raaum O, Naylor R, et al. (2006). American exceptionalism in a new light: a comparison of intergenerational earnings mobility in the Nordic countries, the UK and the US. IZA Discuss. Pap. 1938, Inst. Study Labor, Bonn, Germany.
Johnson, W., Deary, I. J., Silventoinen, K., Tynelius, P., & Rasmussen, F. (2010). Family background buys an education in Minnesota but not in Sweden. Psychological Science, 21, 1266-1273.
Kopczuk, W., Saez, E., & Song, J. (2010). Earnings inequality and mobility in the United States: evidence from social security data since 1937. The Quarterly Journal of Economics, 125(1), 91-128.
Latvala, A., Dick, D.M., Tuulio-Henriksson, A., Suvisaari, J., Viken, R.J., Rose, R.J. ja Kaprio, J. (2011). Genetic Correlation and Gene-Environment Interaction Between Alcohol Problems and Educational Level in Young Adulthood. Journal of Studies on Alcohol and Drugs 72(2): 210-220.
Liu, H., & Zeng, J. (2009). Genetic ability and intergenerational earnings mobility. Journal of Population Economics, 22(1), 75–95.
Marioni RE, Davies G, Hayward C, Liewald D, Kerr SM, Campbell A, Luciano M, Smith BH, Padmanabhan S, Hocking LJ, Hastie ND, Wright AF, Porteous DJ, Visscher PM, Deary IJ (2014). Molecular genetic contributions to socioeconomic status and intelligence. Intelligence, 44, 26-32.
Marks, Gary (2013). Reproduction of economic inequalities: Are the figures for the United States and United Kingdom too high?. Comparative Social Research 30:341-363.
Miller, Paul, Mulvey Charles, & Martin Nick (1995). What do Twin Studies Reveal About the Econmic Returns to Education: a Comparison of Australian and U.S. Findings. American Economic Review 85,3:586–599.
Muller, S. M. (2008). Begging the question: permanent income and social mobility. ERSA Working Paper 75.
Muller, S. M. (2010). Another problem in the estimation of intergenerational income mobility. Economics Letters, 108(3), 291–295.
O’Neill, D., Sweetman, O., & Van de Gaer, D. (2007). The effects of measurement error and omitted variables when using transition matrices to measure inter-generational mobility. Journal of Economic Inequality, 5, 159–178.
Organisation for Economic Co-operation and Development. (2008). Growing unequal? Income distribution and poverty in OECD countries. Report Division of Social Affairs, OECD, Paris, France.
Parman, John M. (2011). American Mobility and the Expansion of Public Education. The Journal of Economic History 71(01), 105-132.
Pekkala Kerr, Sari, Pekkarinen, Tuomas, & Uusitalo, Roope (2013). School tracking and development of cognitive skills. Journal of Labor Economics 31 (3): 577-602.
Raaum, Oddbjørn, Bratsberg Bernt, Røed Knut, Österbacka Eva, Eriksson Tor, Jäntti Markus, and Naylor Robin A. (2007). Marital Sorting, Household Labor Supply, and Intergenerational Earnings Mobility across Countries. The B.E. Journal of Economic Analysis and Policy, Article 7.
Ritchie S.J., Bates T.C., Der G., Starr J.M., Deary I.J., (2013). Education Is Associated With Higher Later Life IQ Scores, but Not With Faster Cognitive Processing Speed. Psychology and Aging, Vol 28(2), Jun 2013, 515-521.
Rodgers, J. L., Kohler, H. P., McGue, M., Behrman, J. R., Petersen, I., Bingley, P., et al. (2008). Education and cognitive ability as direct, mediating, or spurious influences on female age at first birth: Behaviour genetic models fit to Danish Twin data. American Journal of Sociology, 114(Supp), S202–S232.
Rowe David C. (1994). The Limits of Family Influence: Genes, Experience, and Behavior. New York: Guilford Press.
Rowe, D. C., Vesterdal, W. J., & Rodgers, J. L. (1999). Herrnstein’s syllogism: Genetic and shared environmental influences on IQ, education, and income. Intelligence, 26, 405–423.
Saez, E., & Veall, M. R. (2005). The evolution of high incomes in Northern America: lessons from Canadian evidence. American Economic Review, 831-849.
Scarr, S., & Weinberg, R. A. (1994). Educational and occupational achievements of brothers and sisters in adoptive and biologically related families. Behavior Genetics, 24, 301-325.
Schmidt, Frank L., & Hunter John (2004). General Mental Ability in the World of Work: Occupational Attainment and Job Performance. Journal of Personality and Social Psychology 86(1):162-73.
Schnitzlein, D. D. (2014). How important is the family? Evidence from sibling correlations in permanent earnings in the USA, Germany, and Denmark. Journal of Population Economics 27: 69-89.
Silventoinen, K., Sarlio-Lähteenkorva, S., Koskenvuo, M., Lahelma, E., and Kaprio, J. (2004). Effects of Environmental and Genetic Factors on Education-Associated Disparities in Weight and Weight Gain: A Study of Finnish Adult Twins. American Journal of Clinical Nutrition 80(4): 815-822.
Solon, Gary (1992). Intergenerational Income Mobility in the United States. American Economic Review 82, no. 3: 393-408.
Tambs, K., J. M. Sundet, P. Magnus, K. Berg. (1989). Genetic and environmental contributions to the covariance between occupational status, educational attainment and IQ: A study of twins. Behav. Genetics 19 209–222.
Trzaskowski, M., Harlaar, N., Arden, R., Krapohl, E., Rimfeld, K., McMillan, A., et al. (2014). Genetic influence on family socioeconomic status and children’s intelligence. Intelligence, 42, 83–88.
Watkins, M. W., Lei, P.-W., & Canivez, G. L. (2007). Psychometric intelligence and achievement: A cross-lagged panel analysis. Intelligence, 35, 59–68.

Meng Hu on HBD and Austrian Economics

Discussion about this post