IQ Testing : From Correlation to Causation

It is well known and acknowledged that IQ correlates with social outcomes (Herrnstein & Murray, 1994; Jensen, 1980, 1998; Gottfredson, 1997), measures of health (Gottfredson, 2004, & Deary, 2004; Reeve & Basalik, 2010), wages (Jones & Schneider, 2008), savings (Jones, 2012), job performance (Ree & Earles, 1994; Schmidt & Hunter, 2004), training success (Ree & Earles, 1991), general knowledge (Reeve, 2004), general economic performance (Jones & Schneider, 2006; Jones, 2011, 2012; Hafer & Jones, 2012), and this, without mentioning other many correlates of importance (Lynn & Vanhanen, 2012). While IQ critics usually claim that correlational studies tell us nothing about the causal link, there are in fact indirect evidence of a causal link. The present article will introduce some research on this topic.

(Last update : September 2014)

CONTENT [Jump links below]

1. The role of the g factor
2. Confounding factors and competitive theories
3. Processing speed to school achievement
4. Causal path analyses

1. The role of the g factor (test complexity) in predictive validity.

McKay & McDaniel (2006, p. 546) as well as te Nijenhuis & van der Flier (2005) demonstrate, by way of method of correlated vectors, that the cognitive loading of the jobs performed correlates in fact with racial differences. Complexity of the job increases with black-white differences or with minority-majority differences. This is fully consistent with the Spearman-Jensen theory, to the extent that differences increase with g (Jensen, 1998, pp. 377-378). This shows that the importance of g is not reduced to the within-group dimension.

Jensen (1998, pp. 276-277, 280, 283, 286) shows us that subtests’ g-saturations of cognitive batteries are correlated with predictive validity coefficients (i.e., correlation with measures of social outcomes) of those same subtests. In the same way, NLSY97 data shows that ASVAB subtests’ g-loadings correlate with their correlations with (GPA) grade point average (Hu, Sept.21.2013). This holds true whether we look at the black, hispanic or white sample. Furthermore, controlling for both parental income and parental education reduces this correlation just a little.

However, if past research demonstrates the preponderance of g (e.g., Ree & Earles, 1991, 1994), it remains possible that the importance of specific/narrow latent abilities had been underestimated. Reeve (2004) tells us that previous methods employed failed to properly isolate specific cognitive latent factors from the general cognitive latent factor due to variances attributable to random measurement errors : “Often studies of cognitive abilities have relied on the observed subscales of a test (as defined at the discretion of test constructor) as a construct-valid surrogate for narrow ability constructs (e.g., Hunter, 1986; Thorndike, 1991). … studies of the validities of narrow abilities often estimate these factors with the variance due to g included. Thus, the correlations with outcomes reflect both the variance due to g as well as the unique variance due to the specific factor.” (p. 625). Thus he proposes the use of latent variable models with structural modeling equation (SEM) since they would evaluate more precisely these specific abilities (i.e., the latent (non observed) factors are deemed to represent the variance shared by the observed (measured) variables included). The conclusion of his analysis (pp. 635-639) is that the general cognitive latent factor is the predominant predictor of general (not narrow) knowledge, that the specific cognitive latent factors add no additional variance to the general knowledge factor, that the specific factors had correlations with some domains of specific knowledge even if some of these structural path coefficients approach zero. The importance of specific latent abilities on specific criterion of knowledge having been established, he noted : “Although narrow abilities may be important predictors of some narrow criterion factors, this does not necessarily indicate that these criterion factors are practically meaningful. Indeed, the general knowledge factor, which was predicted solely by g, accounts for the majority of the total variance underlying the criterion construct space. Thus, the narrow abilities, despite their evident psychological significance, may only have practical significance in situations where the range of general ability has been restricted (e.g., among a group of doctoral graduate students, where prescreening produces significant range restriction in g).” (pp. 639-640). Finally, one limitation of his study is that some tests of knowledge used have a low reliability and this could have limited somewhat the relationship between factors of specific knowledge and specific abilities.

Reeve (2004) and Coyle (2013) noted that because non-g factors or residuals predict narrow abilities, this pattern is not inconsistent with the investment theory for which non-g ability is assumed to reflect specific skills that contribute to specific abilities. Investing in skills in one domain (e.g., verbal) comes at the expense of developing abilities in other domains (e.g., non-verbal), and this results in negative relations between these (verbal) skills and those other (non-verbal) abilities.

Another SEM study has been conducted, e.g., Brown et al. (2006, Table 5). In this study, three levels of abilities can be distinguished : specific aptitudes (6 ASVAB subtests), general aptitudes (3 latent common factors as the sum of previous six ASVAB subtests), GMA (the equally weighted sum of the 3 general aptitude scores). The authors attempt to test whether specific mental abilities have increment validity for predicting performance above and beyond general mental ability (GMA or g). The specific aptitude theory would predict the pattern displayed in Figure 2 to be the best fit model over Figure 1 while g-theory predicts no better fit for Figure 2. They explain the importance to take care of measurement error in this text :

As noted by Schmidt et al. (1981), theory-driven research should examine validities at the true score or construct level. The true-score level refers to the relationship among the constructs free from measurement error and other statistical biases. Examining validities calculated on imperfect measures often produces an inaccurate picture of the relative importance of the abilities themselves. This occurs because partialling out imperfect measures does not fully partial out the effects of underlying constructs (Schmidt et al., 1981). To illustrate, suppose that Ability A is a cause of training performance but Ability B is not. Suppose further that the tests assessing these abilities have reliabilities of .80 and are positively correlated (as occurs with all mental ability tests). Because Ability B is correlated with Ability A, Ability B will show a substantial validity for training performance. Moreover, because Ability A is not measured with perfect reliability, partialling it from Ability B in a regression analysis would not partial out all of the variance attributable to Ability A. Thus, the measure of Ability B will receive a substantial regression weight when in fact the construct-level regression weight is zero. That is, Ability B will predict training performance even though it is not a true underlying cause of training performance. In this case, Ability B will appear to increment validity over Ability A only because of the presence of measurement error (see also Schmidt & Hunter, 1996).

In fact, the model with 3 general factors has a slightly better model fit than the GMA model. Unlike what the authors said, the GMA model seems to be inferior, at least with the ASVAB. On the other hand, g has higher validity in training programs of higher complexity, as expected. But, importantly, the sample and/or the test has some peculiar features. From Figure 2, it can be seen that verbal and technical don’t correlate at all with training performance. If the inclusion of the second order g factor would have implied to force these two lower factors to correlate with training performance through g, then it may explain why the latent g shows poorer model fit.

Cawley et al. (1996, Tables 7 & 8) analyze the NLSY79, using the ASVAB, on each racial group (blacks, hispanics, whites, each divided in gender groups). PCA is conducted (and yielded 10 PCs) in order to evaluate the correlations of the principal components (PC) with wages. Occupational choice (white vs blue collar) seems to be dominated by PC1 (g) more than PC2 but the latter also is an important factor, especially among whites, somewhat less among hispanics and black males, but absolutely not in the case of black females, where PC1 was the only factor of importance. They also demonstrate in a series of regressions, controlling for education, potential experience, region, unemployment, that PC1 (g) has a good correlation with white collar, while PC1 is not the dominant factor when blue collar was the dependent predictor. This confirms the theories that g deals with complexity. Low-skilled jobs don’t require much of g. Such inferences would be correct however only when we are concerned with the direct (not total) effect of the predictors. Furthermore, when they regress ASVAB (Tables 3GA-3RB) on age, education and parental education, the residualized g does not predict wages anymore. First of all, the authors do not understand that multiple regression only estimates the direct (not full) effect of the independent variables. Secondly, if SES measures are g-loaded, removing these variables from g would necessarily produce a decline in the g-loadedness of the ASVAB. However, g only diminishes in importance among whites, and, to a lesser extent, hispanics, whereas g (PC1) remains very powerful among blacks. In this case, the Spearman law of diminishing return (SLODR) is well supported. Low-IQ people must rely much more on g to achieve high wages than high-IQ people who can rely on some other non-g capabilities because they are less dependent on g.

Following a relative importance and dominance analyses approach (Azen & Budescu, 2003) which allows computation of regression coefficients that add up to the R² model when they are all squared, Lang et al. (2010) analyze the relationship of g (i.e., GMA) and group factor (i.e., narrow) ability (in Thurstone’s PMA) with job performance. General dominance (Cj) and relative weights (εj) are similar and they evaluate the average relative importance of a predictor across all subset regression models. Any given regression coefficient can thus be interpreted as the effect (contribution) by itself and in combination with the other predictors. They use two ways of constructing the factors. In the first method, the factors are measured by forming unit-weighted (unweighted sum) composites of the measures, using formula rwy=ΣRwy/ΣRw1/2*ΣYy1/2. In the second method, a single marker among the observed tests is used to assess each factor of the PMA test. Table 4 shows that GMA has a better Cj (but not εj) than any of the non-g factors, in both methods. Both g and non-g factors are reliably important. Such a result differs greatly from classical multiple regression where non-g factors are usually adding very little to the g factor. Table 6 shows what happens when job is divided into low- and high-complexity. GMA is clearly (among) the most important predictor(s) among high-complexity, especially in Cj weights, but not anymore when jobs are becoming less complex. They believe (p. 632) their result is generalizable to other european countries. They argue that relative weight analysis overcomes the disadvantage of orthogonalized factor models that assume, although unlikely, the first-order (group) factors are uncorrelated.

The critics once claimed that experience in work will become more important over time, but the data shows the opposite. The correlation between experience and performance declines over the years (Schmidt & Hunter, 2004, p. 168) and when job complexity increases (Gottfredson, 1997, p. 83). Furthermore, the predictive validity of IQ (g) does not decline with increases in levels (years) of job experience.

Other evidence that complexity in IQ was the chief ingredient in the correlation of intelligence with success is provided by Ganzach et al. (2013) findings that occupational complexity (and hence high-IQ persons) mediates the correlation between g and income, and that job complexity mediates correlations between IQ and job performance (Gottfredson, 1997, p. 82). The decline in standard deviation (SD) in IQ scores with increasing occupational level also supports this interpretation (Schmidt & Hunter, 2004, p. 163) as it indicates that success is closely related to g, through an increasing minimum cognitive threshold. Another piece of evidence (Schmidt & Hunter, 2004, p. 163) comes from longitudinal studies showing that earlier IQ predicts (later) movement in job hierarchy. Lower-IQ persons move down. Higher-IQ persons move up. Furthermore, when persons’ IQ exceeded their job complexity level, those persons will move up into a higher-complexity job, and vice versa. Ganzach (2011) reached similar conclusions; SES affects job-market success only through entry pay whereas IQ exerts its effect mainly through pay trajectory. Again, this pattern is more consistent with causal-IQ theories than with social theories. This analysis, however, relies on multiple regression, and thus only the direct effects of the predictors are being compared. But if IQ causes education more than the other way, the total effect of IQ relative to education would be under-estimated. One criticism about the SES variable used is that they are not inclusive/sensitive enough, i.e., they miss some important sources of economic background. Ganzach uses 2 measures of SES, narrow and extended (which includes several geographical and familial variables), but their impact were quite similar. Finally, he argues (p. 122) that in a static model, differential measurement error between predictors can be a cause of concern, but in a dynamic approach, the variables measured at an earlier time (t1) serve as control for their relative effect at later time (t2) because the same inaccuracy occurs at both measurement occasions.

2. Causal inferences, confounding factors and competitive theories.

It is obvious that the strength of correlation between IQ and achievement is dependent on a set of aspects of any given society. Such a correlation may be moderated by some institutionalized resource allocation practices, e.g., if the access to job or school would have depended more on cognitive competencies as a requirement for entry (Byington & Felps, 2010). Thus, one should not argue that the correlation needs to be equivalent in all societies and at all times.

Among the many critics of IQ tests, there has been the proposed idea of “threshold hypothesis” which states that beyond a certain level of IQ (e.g., 120), IQ has no correlation with social outcomes. But Jensen (1980, pp. 318-319; 1998, pp. 289-290) indicates several times that this idea is not empirically confirmed because IQ is related linearly with academic achievement at any given level of IQ. We have a graphical illustration of this below :

Still, Lemos et al. (2014) report recent studies showing that IQ becomes less predictive of scholastic achievement at higher levels of education. The first explanation is range restriction in the variation of IQs. The second is the Spearman effect of diminishing return. The strength of g (the subtests intercorrelations) diminishes at higher levels of IQ, and this would account for its lower predictive validity. The third explanation involves Gf-Gc investment theory. Over time, Gc increases at the expense of Gf. Elementary schools focus on exercise of basic processes in perception, memory, reasoning. But as the curriculum grows exponentially in amplitude and complexity, knowledge and experience are requested to a greater extent.

Several studies show that motivation and aspiration are good predictors of scholastic achievement. Lemos et al. (2014) found that aspiration and past academic failures (which can easily condition future motivational levels) have both independent regression coefficients of about 0.15-0.20 on language and math grades, when the latent factor g is controlled. However, the latent g factor (using the 5 speeded subtests of RTB, Reasoning Tests Battery) has a stronger coefficient for math (0.26-0.23) but not for language (0.11/0.14). They took two samples, one of 7-9th graders, one of 10-12th graders. The parameter estimates were generally similar across groups, which does not fit the assumption of the investment theory. One possible reason for the weak independent effect of latent g is that the subtests have a relatively weaker verbal component. In other words, the g is narrowly defined. Their study may somewhat contradict Duckworth & Seligman (2005) study that has found a stronger coefficient for motivation than for IQ on GPA. It is possible that the kind of test truly matters. Duckworth et al. (2012) conduct path analyses using longitudinal data. Their two studies produce similar results; in study 1 the IQ and achievement tests were the Wechsler and WJ-R, and in study 2 the IQ and achievements test were the Raven and a composite of language arts and math. When GPA (or achievement test) is the dependent variable, self-control has a good (or no) independent path when IQ and early GPA (or achievement test) are controlled whereas IQ has a good (or no) independent path when self-control and early achievement test (or GPA) are controlled. Either it means that IQ is poor at predicting GPA or its influence works only through its effect on self-control. Multiple regression techniques don’t answer the question of indirect causal paths but it seems unlikely that motivation can cause intelligence, as it is situation-specific, and, consequently, is certainly devoid of g. The fundamentals are also flawed. Jensen (1980, p. 322) argued that it is success (failure) itself that enhances (dampens) motivation rather than the opposite.

But one of the most used argument is that the correlation between IQ and social outcomes is superfluous because it is confounded by socio-economic status (SES) and other familial-related influences. In reality, even after equating for SES, IQ has still a large effect on social outcomes. The fact that SES has no considerable impact on the correlation between IQ and scholastic tests is illustrated by the partial correlation analyses (with SES partialled out) that tend to reduce just slightly the initial bivariate correlation (Jensen, 1980, p. 336). In analyzing a brazilian sample, Colom & Flores-Mendoza (2007) replicate the Kemp (1955) study cited by Jensen (1980). The zero-order correlations between IQ (Raven) and scholastic achievement were clearly not reduced when partialing out parental SES through path analyses whereas these measures of SES have near zero direct effect on the child achievement (Ns= 372, 100, 169). In the large NCDS data for UK, Thienpont & Verleye (2004) also confirm, through SEM, the strong direct effect of IQ on education and the modest direct effect of parental education on the offspring education. Johnson & Nagoshi (1985) found in the Hawaii Family Study of Cognition (HFSC) that parents’ IQ scores moderate the relationship between child’s IQ and parental education and social background. The relationship between parent and children IQ is also moderated (but probably less) when parental education and social background are controlled. Splitting the samples into low, medium and high SES does not affect parent-offspring IQ correlations (Nagoshi & Johnson, 2005).

A more powerful method involves sibling design. Murray (1998) showed in a large sibling study (NLSY79) that the sibling having the highest (lowest) IQ will end up with a higher (lower) level of socio-economic status relative to the other. Higher IQ among siblings also predict other social outcomes such as lower babies born out of wedlock, greater weeks worked, less fertility, greater age at birth for mothers. Thus, sibling method replicates the research conducted on the NLSY79 and presented in The Bell Curve (1994). Obviously, because siblings share the same parents and thus familial influences, SES-related arguments must be discarded.

Another approach is the adoption design. The failure of adoption studies (e.g., Capron & Duyme, 1989, 1996) to show a Jensen effect (i.e., relationship with g) on adoption gains when low-SES abused children had been adopted by rich families (Jensen, 1997; Hu, Feb.19.2013). A similar conclusion could be drawn from the path analysis that has been done by Rice et al. (1988) study on the biological-adoptive families of the CAP data. They report that environmental familial influences, measured by indices of HOME, on children’s IQ, show direct environmental effects at 1 year of age, and then direct environmental effects as well as indirect genetic effects through parental mediation at 2 years of age, and then only indirect genetic effects at 3 and 4 years of age. This would suggest that environmental influences must be more effective at earliest ages (infancy rather than early childhood). But, at the same time, Sacerdote (2002, Table 1) finds that the percentage of adoptees (N=157) with SAT-Math>500 is not correlated with adoptive parental income or population of the adoptee’s hometown (both entered as independent var.) with a model R² as low as 0.00. All individuals were adopted between the ages 0-3. In general, adoption seems not to have a large impact on adult outcomes. This may be in line with the fact that educational interventions usually fail to improve g on the long run (see, Ritchie et al. 2013).

Another (but crude) way to get an idea of the lower impact of parental SES versus IQ is to observe that IQ correlates more with adult’s attained SES than with his parents’ SES (Jensen, 1973, p. 236, 1998, p. 384; Saunders, 1996, 2002; Strenze, 2007, Table 1, fn. 9). This suggests of course that parental SES is not the driving factor but instead that IQ is determining SES, more than the reverse.

Also, Gottfredson (1997) provided indirect proof that g is likely to be a causal entity. For instance, learning/training does not improve general productivity at job because g itself already accounts for a large explained variance. That makes sense about why learning improves only specific abilities because gains are not transferred to non-trained, novel tasks. Understanding the concept of g as the capacity of dealing with novelty, non-routine tasks, helps us to understand why the many hopes about job training can’t be realist. In parallel, it is consistent with the many failed replications of experiences in working memory training to raise IQ and more specifically g by generalizing the gains to the other, non-trained cognitive tasks (Hu, Nov.1.2012). As Murray (2005) already explained :

Suppose you have a friend who is a much better athlete than you, possessing better depth perception, hand-eye coordination, strength, and agility. Both of you try high-jumping for the first time, and your friend beats you. You practice for two weeks; your friend doesn’t. You have another contest and you beat your friend. But if tomorrow you were both to go out together and try tennis for the first time, your friend would beat you, just as your friend would beat you in high-jumping if he practiced as much as you did.

Furthermore, Gottfredson points out (1997, pp. 86, 91-92, 108) how it is difficult to reduce individual differences in performance by way of training and learning, insofar as those differences can be magnified instead of decreasing (see also, Ceci & Papierno, 2005). The reason is that intelligent people learn at a faster rate, even when all employees were exposed to the same instruction. Needless to say, this is entirely consistent with the concept of a causal g but not with theories implying that g is built from the outside.

The idea of g as a causal entity has been questioned. It has been proposed that a model of mutualistic causation across specific abilities can account for the presence of g, thus the g is an emergent but not a latent factor (van der Maas et al., 2006). Such a model predicts that the intercorrelation between the tests will be low(er) at early ages, because g(-loading) takes some time to develop. When the prediction has been tested, it failed (Gignac, 2014). Thus, until now, g seems to remain a valid latent construct (Panizzon et al., 2014). Even if g was found not to be a valid (latent) construct, this only raises a problem for g-theories but does not resolve issues about whether IQ causes achievement or the reverse.

3. Processing speed to school achievement.

Now, regarding the possible mechanisms related to IQ-achievement correlation, processing speed is likely to be a good candidate. According to Jensen (1998, 2006), processing speed could well be the purest manifestation of g insofar as it reflects the quality of information processing in the brain which is important in light of the Spearman’s hypothesis because it seems that ECT mediates black-white differences on IQ (Pesta & Poznanski, 2008). We already know there is a significant correlation between IQ and processing speed (Jensen, 1998, pp. 234-238, 2006, pp. 160, 171-172, 195; see also, Grudnik & Kranzler, 2001; Sheppard & Vernon, 2008), that this correlation was almost entirely mediated by genetic factors (Jensen, 1998, p. 233, 2006, pp. 130-131; Lee et al., 2012), that elementary cognitive tasks are less amenable to cultural, learning and personality factors (Rindermann & Neubauer, 2001) while the latter did not predict processing speed (see also, Jensen, 2006, pp. 175-178), thus making these tests an even better measure of intelligence.

And yet we have to determine to what extent speed may be related to achievement through pathways independent of IQ test. First of all, Luo & Petrill (1999) showed that psychometric g and chronometric g are similar in the sense that the intrinsic nature of g is not altered when ECTs are added to the traditional psychometric tests. It also appears that the memory processing component contributes substantially to g estimates. Next, Luo et al. (2003a) found that CAT group factors (as opposed to the general factor) are not important in predicting achievement (measured by MAT), while at the same time the g factor derived from CAT (call it CAT-g) affects achievements measures essentially through the genetic paths, as assessed by the more substantial Chi-square changes (to assess model-fit) for the genetic path than for the shared and non-shared paths (Table 8 below). Subsequently, Luo et al. (2003b) were able to demonstrate that psychometric g, as measured by WISC (call it WISC-g), while being correlated with achievement (MAT variables), was substantially mediated by processing speed (as measured by CAT). In addition, some nonchronometric, memory processing measures had high loadings on the mental speed component. Overall, such findings were coherent with Jensen’s theory of mental speed (see, Jensen, 2006, pp. 212, 216-217, 224, 226-227) which also predicts synergistic interaction between memory processes and speed. The reason could be that information processing speed allows one to consolidate more of the information to which they are exposed in long-term memory (LTM). Besides, the concept of consolidated IQ gains vs. non consolidated gains had been explained by Jensen (1973, pp. 79-97) as being the mechanism behind the increase in IQ heritability with age.

Consistent with Dasen Luo’s conclusions, Rindermann & Neubauer (2004, pp. 581-586) estimated that the direct effect of processing speed of information on scholastic performance is close to zero when intelligence and creativity are partialled out. As shown by Rindermann et al. (2011), mental speed has a non-trivial direct effect on writing ability/literacy, controlling for intelligence and parental education and books at home, even though the impact of intelligence is much stronger than speed, when a latent variable approach is conducted. Although parents’ education and books at home are correlated with speed, it may not necessarily be through environmental but genetic pathways. Rohde & Thompson (2007) have been able to show that specific cognitive abilities such as processing speed, working memory, and spatial ability have a non-trivial direct effect on the scholastic performance (as measured by GPA, SAT-verbal, SAT-math, WRAT-III) but intelligence (as measured by Raven and a Vocabulary test) also has a good portion of its effect that is direct. Another study, by Vock et al. (2011), reports that mental speed has a weak direct impact on academic performance when reasoning and divergent thinking (DT, an index of creativity) are controlled, while short-term memory (STM) has a modest direct effect when reasoning and divergent thinking are controlled. Interestingly, the correlation between mental speed and reasoning diminishes when short-term memory has been controlled, perhaps because these two variables share a common variance. The authors recall however regarding short-term memory that only the active storage (as opposed to passive storage) serves as a good predictor of general cognitive ability or scholastic performance. It was previously demonstrated by Preckel et al. (2011) that speed has a similar correlation with both speeded and unspeeded reasoning tests, either through correlations or SEM regressions. Dodonova & Dodonov (2013) found that processing speed and intelligence each have a non-trivial direct effect on school achievement. One possible reason for this discrepancy with previous studies is due to the modest correlation between intelligence and speed, thus when both are held constant, they still have meaningful direct paths toward achievement.

The importance of processing speed as a mediator of g has been highlighted by Coyle et al. (2011) in the large NLSY97 sample. They found that the direct path from age to the development of g was close to zero. Instead, the improvement of processing speed (PS) was associated with increases in g (over the course of development) and the effect of age on g was virtually fully mediated by processing speed, proxied by using the 2 speeded tests of the ASVAB. The study may have problems though. Jensen (1998, pp. 224, 236-237) mentioned that the 2 speeded subtests of the ASVAB are, among all ASVAB subtests, the least correlated with reaction time and inspection time. Jensen argues that these sorts of tests must be better called “test-taking speed” which is (or may be) different from what the ECTs measure. A similar pattern has also been observed previously in Kail (2007). And, again, the problem is that Kail uses a speeded psychometric test (two subtests of the Woodcock-Johnson) instead of ECT-like tests. At the very least, Kail found that the best model in which age, PS, WM are predictors of Raven at time 1 and time 2, was one where age and PS don’t predict either Raven T1 or T2. But WM has a direct effect on Raven T1 and Raven T2 (controlling for Raven T1). Nettelbeck (2010) managed to replicate Kail (2007) earlier SEM study in which age predicts PS, which predicts working memory (WM) capacity which in turn predicts higher reasoning ability (e.g., as measured by Raven’s or Cattell Culture Fair Test). This model appeared to better fit the data. Besides, in Nettelbeck’s sample, aged adults have seen a decline in reasoning ability due to slower processing speed but also by age-related factors influencing working memory but independent from processing speed. But Nettelbeck study is not without problems either. It must be known that cross-sectional data, instead of longitudinal data, as was the case in Kail (2007), does not lead to correct causal inferences, as there is no time elapsing between the measures (Cole & Maxwell, 2003).

Further considerations had been provided by Demetriou et al. (2013a, pp. 40-44; see also, Coyle, 2013; Kail, 2013; Pascual-Leone, 2013; Demetriou et al., 2013b, 2013c) SEM analyses which established that processing speed predicts g-fluid better than working memory during transitional periods when new mental abilities were created whereas working memory predicts g-fluid better than speed during stable periods when existent abilities are consolidated and more strongly related to each other. Both PS and WM are relevant because speed of processing allows people to handle information flow more efficiently during problem solving whereas working memory allows people to represent and process more information units at the same time. In general, the description of their analyses (for the study in the middle childhood phase) may be best summarized as follows :

In the model fit on the longitudinal data, we used the speed and the working memory scores of the first testing wave and the gf scores of the second testing wave. That is, in the first group, speed and WM at 6, 7, or 8 are used to predict gf at 7, 8, and 9 years. In the second group, speed and working memory at 9 or 10 are used to predict gf at 10 or 11 years. To test the assumption that the structure of abilities does not vary with time but their relations might vary, we constrained all relations between measures and factors to be equal across the two groups and we let the structural relations vary freely. It is recognized that the relatively small number of participants in the two age blocks compared may weaken the statistical power of structural relations. To compensate for this problem the number of measurement in these models was kept to a minimum.

The fit of this model was excellent (see Table 1). The relations between constructs are patterned as expected. In the younger age group, the relations between age and speed (−.71), and gf (.48) were significant and much higher than in the older age group (−.14 and 0, respectively). However, the relations between working memory and speed and working memory and gf were much higher in the older (−.44 and .64) than in the younger age group (−.28 and .49, respectively). Thus, it seemed that in the first phase speed reflected age changes because in this phase children became extensively faster in processing and relatively better in gf. In the next phase, gf changes converged increasingly with working memory, reflecting an across the board expansion of thought towards the capacity indexed by WM.

This has implications for the Spearman’s law of diminishing returns for age (SLODR-age) since increasing g “results in differentiation of cognitive abilities because excessive g allows for investment into domain-specific learning, thereby fostering domain autonomy” (p. 38) which tends to converge with Woodley (2011) CD-IE thesis. Demetriou’s general discussion is worth citing as well :

Our findings about structure confirmed both the SLODRage prediction that cognitive processes differentiate from each other (prediction 4a) and the developmental prediction that they become increasingly coordinated with each other (prediction 4b). Differentiation was suggested by the fact that, with age, different types of mental processes are expressed through process-specific factors rather than through a more inclusive representational factor. These process specific factors tended to relate increasingly with a general factor at a subsequent phase, reflecting an integration of previously differentiated processes. This concurrent differentiation/integration of cognitive processes necessitates a redefinition of the nature of cognitive development. Our findings suggested that intellectual power increases with development because cognitive processes and reasoning evolve through several cycles of differentiation and integration where relations are dynamic and bidirectional. According to the present and other research (Demetriou, 2000; Demetriou & Kazi, 2001, 2006; Flavell, Green, & Flavell, 1995), differentiation goes from general cognitive functions to specific cognitive processes and mental operations. Integration follows the trend, focusing on increasingly specific processes and operations. Differentiation of cognitive processes allows their control because they may be individually regulated according to a goal-relevant plan. Integration of mental operations generates content-free inferential schemes that can be brought to bear on truth and validity. In both differential and developmental theories, the differentiation/integration process always applies on inferential processes. Moreover, in developmental theory, the state of their coordination frames the functioning of all other cognitive processes, such as language, mental imagery, and memory, imposing a stage-specific overall worldview (Piaget, 1970).

At the biological level, Penke et al. (2012, Figure 2) conducted SEM analysis to test the possible pathways from three different indicators of white matter tract integrity to general intelligence (g). They discovered that this path was fully mediated by information-processing speed. They made this assumption since efficient information processing between distal brain regions is thought to rely on the integrity of their interconnecting white matter tracts. Well-connected white matter favors efficient information processing. See also Jung & Haier (2007) who emphasized on brain functional connectivity to explicate the neural basis of intelligence.

4. Causal path analyses.

IQ-achievement tests of causality are the most needed and unfortunately rare. Watkins et al. (2007) conducted such a test using SEM to estimate the arrow of causality of IQ (test) latent factors and achievement (test) latent factors across two points in time. In sum, a cross-lagged path analysis. Their model 2 (M2) in which each of the IQ latent factors at Time #1 had direct paths to both IQ latent factors and achievement latent factors at Time #2 (with Achievement1→IQ2 path being not significant) has been selected as the best-fit model to the data, whereas alternative models (e.g., M3, which assumes direct path from achievement latent factor Time #1 on both achievement latent factor and IQ latent factor at Time #2) were not.

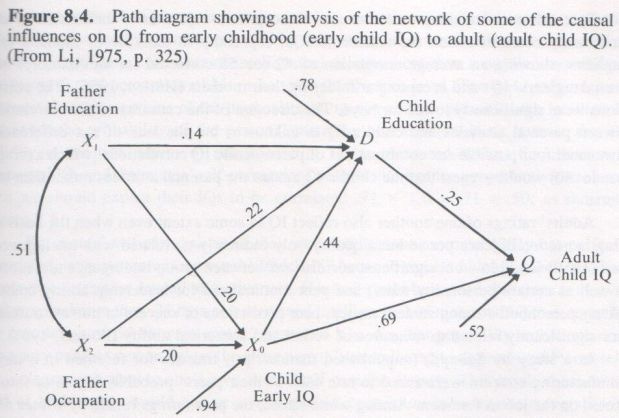
Previous studies of the same nature, although rare, are consistent with Watkins (2007). Jensen (1980, pp. 241, 324, 336-337) cited a study by Crano (1972) although its critics had been summarized by Watkins, notably blaming this study for employing weak methodologies, as Rogosa (1980) detailed. The other cited study was a path coefficient analysis by Li (1975) as shown below :

If father education and occupation each have a direct coefficient of 0.20, this implies that the two variables explain 0.20^2+0.20^2=0.08 or 8% of variation in childhood IQ. But R² constantly under-estimate the true effect size. Moreover, to the extent that the coefficient from childhood IQ to childhood education is 0.44, the coefficient from childhood education to adult IQ being 0.25, then the indirect effect of education on adult IQ would be estimated at 0.44*0.25=0.11 or 11% of the variance. Apparently, education wasn’t really a strong causal determinant. The problem with the methodology is the absence of controlled repeated measures over time (Cole & Maxwell, 2003).

Consistent with the idea that SES is not of so great importance, Brodnick & Ree (1995) investigated the structural relationship between g (SATm, SATv, ACT) and SES (income, family size, parent’s age) and academic performance (AP, diverse GPAs) by way of CFAs. Among these 3 latent variables, they found that SES had no explanatory power. The model which best explained the data is a model g+AP in which there was no direct path connecting the 3 SES observed variables or even the SES common latent factor to the latent AP or its observed elements. g has a path of 0.672 going to AP, thus accounting for 0.672² or 45.2% of variance in AP, with D being the unexplained variance of AP which is 0.740² or 54.8% (i.e., 45.2%+54.8%=100%). Because a g-only model shows no fit decrement as compared with a g+SES model, this would mean that using a separate SES latent variable when g had been incorporated is not very useful. That the authors used SAT/ACT to derive a latent g might be questional to some, but Frey & Detterman (2004), Koenig et al. (2008), and Coyle & Pillow (2008) confirmed that SAT and ACT are good proxies of g. But this result may be explained by statistical artifacts, precisely, that family size and parental age are inaccurate measures of SES, hence the absence of increment in model fit when latent SES is added. In the NLSY97, this couldn’t be replicated but the independent impact of adolescents’ intelligence was stronger than the independent impact of parental SES on outcome.

References.

1. Brown K.G., Le H., & Schmidt F.L. (2006). Specific Aptitude Theory revisited: Is there incremental validity for training performance?. International Journal of Selection and Assessment, 14, 87–100.

2. Byington, E., & Felps, W. (2010). Why do IQ scores predict job performance?: An alternative, sociological explanation. Research in Organizational Behavior, 30, 175-202.

3. Cawley J., Coneely K., Heckman J., & Vytlacil E. (1996). Measuring the Effects of Cognitive Ability. NBER Working Paper No. 5645, July 1996.

4. Ceci, S.J., & Papierno, P.B. (2005). The rhetoric and reality of gap closing: When the “have nots” gain but the “haves” gain even more. American Psychologist, 60, 149–160.

5. Colom, R., & Flores-Mendoza, C. E. (2007). Intelligence predicts scholastic achievement irrespective of SES factors: Evidence from Brazil. Intelligence, 35, 243-251.

6. Coyle, T.R., & Pillow, D. R. (2008). SAT and ACT predict college GPA after removing g. Intelligence, 36, 719–729.

7. Coyle, T. R., Pillow, D. R., Snyder, A. C., & Kochunov, P. (2011). Processing speed mediates the development of general intelligence in adolescence. Psychological Science, 22, 1265–1269.

8. Coyle, T.R., Snyder, A.C., Purcell, J.M., & Kochunov, P. (2013). Non-g residuals of the SAT and ACT predict specific abilities. Intelligence, 41, 114–120.

9. Coyle, T. R. (2013). Effects of processing speed on intelligence may be underestimated: Comment on Demetriou et al. (2013). Intelligence, 41(5), 732–734.

10. Demetriou, A., Spanoudis, G., Shayer, M., Mouyi, A., Kazi, S., & Platsidou, M. (2013a). Cycles in speed-working memory-G relations: Towards a developmental-differential theory of mind. Intelligence, 41, 34–50.

11. Demetriou, A., Spanoudis, D., & Shayer, M. (2013b). Developmental intelligence: From empirical to hidden constructs. Intelligence, 41, 744–749.

12. Demetriou, A., Spanoudis, D., & Shayer, M. (2013c). Developing intelligence: Is a comprehensive theory possible?. Intelligence, 41, 730–731.

13. Duckworth, A. L., & Seligman, M. E. (2005). Self-discipline outdoes IQ in predicting academic performance of adolescents. Psychological science, 16(12), 939-944.

14. Duckworth, A. L., Quinn, P. D., & Tsukayama, E. (2012). What No Child Left Behind leaves behind: The roles of IQ and self-control in predicting standardized achievement test scores and report card grades. Journal of educational psychology, 104(2), 439.

15. Ganzach, Y. (2011). A dynamic analysis of the effects of intelligence and socioeconomic background on job-market success. Intelligence, 39(2), 120–129.

16. Ganzach, Y., Gotlibobski, C., Greenberg, D., & Pazy, A. (2013). General mental ability and pay: Nonlinear effects. Intelligence, 41(5), 631–637.

17. Gignac, G. E. (2014). Dynamic mutualism versus g factor theory: An empirical test. Intelligence. 42, 89-97.

18. Gottfredson, L. S. (1997). Why g matters: The complexity of everyday life. Intelligence 24:79–132.

19. Gottfredson, L. S. (2004). Intelligence: Is it the epidemiologists’ elusive “fundamental cause” of social class inequalities in health?. Journal of Personality and Social Psychology, 86, 174−199.

20. Grudnik, J. L., & Kranzler, J. H. (2001). Meta-analysis of the relationship between intelligence and inspection time. Intelligence, 29, 523–535.

21. Herrnstein, R. J., & Murray, C. (1994). The Bell Curve: Intelligence and Class Structure in American Life. NY: Free Press.

22. Jensen, A. R. (1980). Bias in Mental Testing. New York: Free Press.

23. Jensen, A. R. (1998). The g Factor: The Science of Mental Ability. Westport, CT: Praeger.

24. Jensen, A. R. (2006). Clocking the Mind: Mental Chronometry and Individual Differences. Elsevier.

25. Johnson, R. C., & Nagoshi, C. T. (1985). Parental ability, education, and occupation as influences on offspring cognition in Hawaii and Korea. Personality and Individual Differences, 6, 413-423.

26. Jung, R. E., & Haier, R. J. (2007). The parieto-frontal integration theory (P-FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci 30:135–154, discussion 154–187.

27. Kail, R. V. (2007). Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychological Science, 18, 312–313.

28. Kail, R. V. (2013). Developmental analyses of individual differences in intelligence: Comments on Demetriou, Spanoudis, Shayer, Mouyi, Kazi, and Platsidou (2013). Intelligence, 41, 735–737.

29. Koening, K. A., Frey, M. C., & Detterman, D. K. (2008). ACT and general cognitive ability. Intelligence, 36, 153–160.

30. Lang, J. W., Kersting, M., Hülsheger, U. R., & Lang, J. (2010). General mental ability, narrower cognitive abilities, and job performance: The perspective of the nested-factors model of cognitive abilities. Personnel Psychology, 63(3), 595-640.

31. Lemos, G. C., Abad, F. J., Almeida, L. S., & Colom, R. (2014). Past and future academic experiences are related with present scholastic achievement when intelligence is controlled. Learning and Individual Differences, 32, 148-155.

32. Luo, D., & Petrill, S. A. (1999). Elementary cognitive tasks and their roles in g estimates. Intelligence, 27, 157–174.

33. Luo, D., Thompson, L. A., & Detterman, D. K. (2003a). Phenotypic and behavioral genetic covariation between elemental cognitive components and scholastic measures. Behavior Genetics, 33, 221–246.

34. Luo, D., Thompson, L. A., & Detterman, D. K. (2003b). The causal factor underlying the correlation between psychometric g and scholastic performance. Intelligence, 31, 67–83.

35. Lynn, R., & Vanhanen, T. (2012). National IQs: A review of their educational, cognitive, economic, political, demographic, sociological, epidemiological, geographic and climatic correlates. Intelligence, 40(2), 226–234.

36. McKay, P. F., & McDaniel, M. A. (2006). A reexamination of black-white mean differences in work performance: more data, more moderators. J. Appl. Psychol 2006;91:538–554.

37. Murray, C. (1998). Income inequality and IQ. Washington, DC: AEI Press.

38. Murray, C. (2005). The Inequality Taboo.

39. Nagoshi, C. T., & Johnson, R. C. (2005). Socioeconomic status does not moderate the familiality of cognitive abilities in the Hawaii Family Study of Cognition. Journal of Biosocial Science, 1−9.

40. Nettelbeck, T., & Burns, N. R. (2010). Processing speed, working memory and reasoning ability from childhood to old age. Personality and Individual Differences, 48, 379–384.

41. Pascual-Leone, J. (2013). Can we model organismic causes of working memory, efficiency and fluid intelligence? A meta-subjective perspective. Intelligence, 41, 738–743.

42. Penke, L., Muñoz Maniega, S., Murray, C., Gow, A. J., Hernández, M. C., Clayden, J. D., Starr, J. M., Wardlaw, J. M., Bastin, M. E., and Deary, I. J. (2010). A general factor of brain white matter integrity predicts information processing speed in healthy older people. J. Neurosci. 30, 7569–7574.

43. Penke L, Maniega SM, Bastin ME, Valdes Hernandez MC, Murray C, et al. (2012) Brain white matter tract integrity as a neural foundation for general intelligence. Mol Psychiatry 17: 1026–1030.

44. Pesta, B., & Poznanski, P. (2008). Black–white differences on IQ and grades: The mediating role of elementary cognitive tasks. Intelligence, 36, 323–329.

45. Ree, M. J., & Earles, J. A. (1991). Predicting training success: Not much more than g. Personnel Psychology, 44, 321–332.

46. Ree, M. J., Earles, J. A., & Teachout, M. S. (1994). Predicting job performance: Not much more than g. Journal of Applied Psychology, 79, 518–524.

47. Reeve, C. L. (2004). Differential ability antecedents of general and specific dimensions of declarative knowledge: More than g. Intelligence, 32(6), 621−652.

48. Reeve, C. L., & Basalik, D. (2010). Average state IQ, state wealth and racial composition as predictors of state health statistics: Partial support for ‘g’ as a fundamental cause of health disparities. Intelligence, 38, 282–289.

49. Rice, T., Fulker, D.W., DeFiles, J.C., & Plomin, R. (1988). Path analysis of IQ during infancy and early childhood and an index of the home environment in the Colorado Adoption Project. Intelligence, 12, 27-45.

50. Rindermann, H., & Neubauer, A. C. (2001). The influence of personality on three aspects of cognitive performance: processing speed, intelligence and school performance. Personality and Individual Differences, 30, 829–842.

51. Ritchie S.J., Bates T.C., Der G., Starr J.M., Deary I.J., (2012). Education Is Associated With Higher Later Life IQ Scores, but Not With Faster Cognitive Processing Speed. Psychology and Aging, Vol 28(2), Jun 2013, 515-521.

52. Sacerdote, B. (2002). The Nature and Nurture of Economic Outcomes. American Economic Review, 92(2): 344-348.

53. Saunders, P. (1996). Unequal but fair?: A study of class barriers in Britain. London, UK: IEA.

54. Saunders, P. (2002). Reflections on the meritocracy debate in Britain: a response to Richard Breen and John Goldthorpe. British Journal of Sociology, 53, 559-574.

55. Schmidt, Frank L., & Hunter John (2004). General Mental Ability in the World of Work: Occupational Attainment and Job Performance. Journal of Personality and Social Psychology 86(1):162-73.

56. Sheppard, L. D., & Vernon, P. A. (2008). Intelligence and speed of information-processing: A review of 50 years of research. Personality and Individual Differences, 44, 535–551.

57. Strenze, T. (2007). Intelligence and socioeconomic success: A meta-analytic review of longitudinal research. Intelligence, 35, 401–426.

58. Te Nijenhuis, J., & Van der Flier, H. (2005). Immigrant-majority group differences on work-related measures: The case for cognitive complexity. Personality and Individual Differences, 38, 1213−1221.

59. Thienpont, K., & Verleye, G. (2004). Cognitive ability and occupational status in a British cohort. Journal of Biosocial Science, 36, 333-349.

60. van der Maas, H. L. J., Dolan, C. V., Grasman, R. P. P. P., Wicherts, J. M., Huizenga, H. M., & Raijmakers, M. E. J. (2006). A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review, 113, 842–861.

61. Watkins, M. W., Lei, P.-W., & Canivez, G. L. (2007). Psychometric intelligence and achievement: A cross-lagged panel analysis. Intelligence, 35, 59–68.

62. Woodley, M. A. (2011b). The cognitive differentiation–integration effort hypothesis: A synthesis between the fitness indicator and life history models of human intelligence. Review of General Psychology, 15, 228–245.